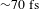1 Introduction
Recently, more and more attention has been paid on high repetition rate (HRR)
$({>}1~\text{MHz})$
high harmonics generation (HHG). Thus far, configurations, such as external seeded femtosecond enhancement cavity (fsEC) based HHG[Reference Gohle, Udem, Herrmann, Rauschenberger, Holzwarth, Schuessler, Krausz and Hänsch1–Reference Ozawa, Rauschenberger, Gohle, Herrmann, Walker, Pervak, Fernandez, Graf, Apolonski, Holzwarth, Krausz, Hansch and Udem3], high power high repetition rate lasers based single pass HHG[Reference Vernaleken, Weitenberg, Sartorius, Russbueldt, Schneider, Stebbings, Kling, Hommelhoff, Hoffmann, Poprawe, Krausz, Hänsch and Udem4–Reference Klas, Demmler, Tschernajew, Hädrich, Shamir, Tünnermann, Rothhardt and Limpert6] and HHG inside a mode locked Ti:sapphire oscillator and thin disk oscillators[Reference Seres, Seres and Spielmann7–Reference Kanda, Imahoko, Yoshida, Eilanlou, Nabekawa, Sumiyoshi, Kuwata-Gonokami and Midorikawa9], have been demonstrated. Comparatively speaking, external seeded fsEC has relatively lower requirements on the seed laser itself in terms of the peak power, which can rely on the external enhancement cavity to achieve the needed peak power for HHG. Therefore fsEC has the best performance on the repetition rate scaling, up to 250 MHz to date[Reference Carstens, Högner, Saule, Holzberger, Lilienfein, Guggenmos, Jocher, Eidam, Esser, Tosa, Pervak, Limpert, Tünnermann, Kleineberg, Krausz and Pupeza10]. For single pass HHG and thin disk oscillator based intra-cavity HHG, much more efforts have to be put to develop laser drivers with higher peak power. HHG at such high repetition rates (
${\sim}250~\text{MHz}$
) is so far difficult to achieve for single pass or intra-oscillator HHG because of insufficient pulse energy. Single pass HHG at 20.8 MHz and intra-disk-oscillator HHG at 17.8 MHz have been demonstrated[Reference Vernaleken, Weitenberg, Sartorius, Russbueldt, Schneider, Stebbings, Kling, Hommelhoff, Hoffmann, Poprawe, Krausz, Hänsch and Udem4, Reference Labaye, Gaponenko, Wittwer, Diebold, Paradis, Modsching, Merceron, Emaury, Graumann, Phillips, Saraceno, Kränkel, Keller and Südmeyer8].
FsEC based HHG was demonstrated first in 2005, and has been established as an effective method to achieve HRR vacuum ultraviolet (VUV) frequency combs[Reference Gohle, Udem, Herrmann, Rauschenberger, Holzwarth, Schuessler, Krausz and Hänsch1–Reference Ozawa, Rauschenberger, Gohle, Herrmann, Walker, Pervak, Fernandez, Graf, Apolonski, Holzwarth, Krausz, Hansch and Udem3]. Even without being stabilized as a frequency comb, an fsEC can be regarded as a tool to efficiently convert low power near infrared (NIR) pulsed sources into HRR
$({>}10~\text{MHz})$
VUV lasers. This type of HRR VUV laser is essential for boosting the acquisition speed of angle-resolved photoelectron spectroscopy (ARPES) measurements in a space-charge-free condition[Reference Chiang, Huth, Trützschler, Kiel, Schumann, Kirschner and Widdra11]. Recently, Mills et al. have shown the usability of fsEC based extreme ultraviolet (XUV) source for time-resolved femtosecond photoemission spectroscopy at 60 MHz[Reference Mills, Zhdanovich, Boschini, Na, Schneider, Dosanjh, Wong, Levy, Damascelli and Jones12]. We recently also demonstrated a high power 149 nm VUV laser with a 10 MHz repetition rate using an fsEC seeded by a
${\sim}200~\text{fs}$
Yb-fiber-based fiber chirped pulse amplifier (FCPA)[Reference Ozawa, Zhao, Kuwata-Gonokami and Kobayashi13], which could deliver an average power of 0.2 mW. For many applications where a high temporal resolution is required, pulse durations shorter than the one demonstrated in Ref. [Reference Ozawa, Zhao, Kuwata-Gonokami and Kobayashi13] would be preferred. In IR-XUV ARPES experiments with time resolution shorter than 100 fs, collisions between electrons and various vibrionic modes become visible in real time[Reference Krausz and Ivanov14]. On the other hand, a shorter pulse duration results in a broader spectral bandwidth, which deteriorates the energy resolution when applied to ARPES. To make our system compatible with both applications demanding high energy resolution (as provided by
${\sim}200~\text{fs}$
pulses) and high temporal resolution (as enabled by sub-hundred fs pulses), we improved the original fsEC[Reference Ozawa, Zhao, Kuwata-Gonokami and Kobayashi13] to offer shorter pulse durations, so that one can easily choose high temporal or spectral resolution, depending on the applications. In addition, where fsEC technology is concerned, shorter pulse durations help to relax the problem of significant ionization of the HHG-medium, which can clamp the effective peak intensity and prevent VUV power scaling[Reference Pupeza, Holzberger, Eidam, Carstens, Esser, Weitenberg, Rußbüldt, Rauschenberger, Limpert, Udem, Tünnermann, Hänsch, Apolonski, Krausz and Fill15].
Figure 1. Schematic of the experimental setup, which consists of an Yb-fiber-based CPA driving laser, an LMA fiber based pulse compressor, PDH locking electronics and a large-scale bow-tie enhancement cavity.
Due to the narrower gain bandwidth, compared with that of Ti:sapphire crystals, and the gain narrowing effect of high gain amplifiers, Yb-fiber-based chirped pulse amplifier (CPA) lasers usually offer longer pulse durations than their Ti:sapphire laser counterparts. However, Yb-fiber lasers can be pumped with high power laser diode and provide higher average output powers than Ti:sapphire systems, thanks to their high gain and high surface area to volume ratio, which allows efficient cooling. Thus far, the shortest pulse duration of 145 fs was demonstrated for a
$6~\unicode[STIX]{x03BC}\text{J}$
Yb-based linear FCPA at 1030 nm[Reference Wunram, Storz, Brida and Leitenstorfer16]. With a linear FCPA and by shifting the central wavelength to 1070 nm, 120 fs was achieved with a pulse energy of
${\sim}0.5~\unicode[STIX]{x03BC}\text{J}$
and a repetition rate of 154 MHz[Reference Ruehl, Marcinkevicius, Fermann and Hartl17]. Using the pre-chirp method, which itself is a type of nonlinear CPA, pulses with a duration of 60 fs, an energy of
$1.33~\unicode[STIX]{x03BC}\text{J}$
and a repetition rate of 75 MHz were realized[Reference Liu, Schimpf, Eidam, Limpert, Tünnermann, Kärtner and Chang18]. Instead of shortening the pulse durations directly from the FCPA, another popular way is via post-compression using various fibers[Reference Baltuska, Wei, Pshenichnikov and Wiersma19–Reference Bohman, Suda, Kanai, Yamaguchi and Midorikawa21]. The mechanism is attributed to spectral broadening through self-phase modulation (SPM) inside the fiber, followed by removal of the residual phase using grating pairs or chirped mirrors. This method of post-compression can be conveniently added to existing laser systems. Depending on the initial pulse energy and the target pulse duration, fibers of different core sizes and lengths can be selected. For
${\sim}\text{nJ}$
[Reference Baltuska, Wei, Pshenichnikov and Wiersma19] and
${\sim}\unicode[STIX]{x03BC}\text{J}$
[Reference Südmeyer, Brunner, Innerhofer, Paschotta, Furusawa, Baggett, Monro, Richardson and Keller20] pulses, single mode and large mode area (LMA) fibers can be utilized, respectively. For higher pulse energy of
${\sim}\text{mJ}$
levels, hollow core fibers have been used[Reference Bohman, Suda, Kanai, Yamaguchi and Midorikawa21].
In this contribution, we report an efficient VUV (
$\unicode[STIX]{x03BB}\sim 149~\text{nm}$
, i.e.,
${\sim}8.3~\text{eV}$
) laser beam delivered by a 10 MHz fsEC, seeded by a
${\sim}70~\text{fs}$
post-compressed Yb-based FCPA laser. Stable operation lasting over 30 min with more than 0.1 mW of outcoupled power at 149 nm was demonstrated using a low finesse enhancement cavity. It was found that shorter pulse was beneficial for alleviating the nonlinear plasma effect and improving the efficiency of HHG. Low finesse cavity can also relax the plasma nonlinearity clamped intra-cavity power and improve the cavity-locking stability. Since the seed pulse duration at 1040 nm was characterized to be
${\sim}70~\text{fs}$
, we expected sub-50 fs pulse durations for 149 nm pulses, because the pulse duration
$\unicode[STIX]{x1D70F}_{q}$
is comparable to, and in general expected to be smaller than, that of the driving field
$\unicode[STIX]{x1D70F}_{0}$
, behaving approximately as
$\unicode[STIX]{x1D70F}_{q}\sim \unicode[STIX]{x1D70F}_{0}/q^{1/2}$
for lower order harmonics, where
$q$
is the harmonic order[Reference Muffett, Wahlstrom and Hutchinson22]. These performance characteristics are an extension of our original system[Reference Ozawa, Zhao, Kuwata-Gonokami and Kobayashi13] and such short pulses should enable applications such as time-resolved coincidence experiments at high repetition rates or time-resolved photoelectron spectroscopy.
Figure 2. (a) Optical spectra of FCPA output (blue) and compressed pulses (red). (b) Temporal pulse shapes as measured by FROG for original pulses from the FCPA (blue) and externally compressed pulses (red). (c) Output power (red) and total efficiency (blue) of the external pulse compression stage, including dispersion compensation. (d) Beam profile of the compressed laser pulses.
2 Experiments and results
The schematic of the entire experimental setup is shown in Figure 1: an Yb-fiber-based FCPA driving laser, an LMA fiber based pulse compressor, Pound-Drever-Hall (PDH) locking electronics and a large-scale bow-tie enhancement cavity.
Here, the driver was an Yb-based linear FCPA laser with a maximum compressed output power of 23 W, a repetition rate of 10 MHz, a pulse duration of
${\sim}200~\text{fs}$
and a central wavelength of 1040 nm[Reference Kobayashi, Hirayama, Ozawa, Sukegawa, Seki, Kuramoto and Watanabe23]. The laser source featured high efficiency large-scale (
$180~\text{mm}\times 40~\text{mm}\times 1~\text{mm}$
) transmission gratings used in both the pulse stretcher and compressor. This driving laser, in combination with a 10 MHz fsEC, was shown to provide
$30~\unicode[STIX]{x03BC}\text{W}$
of outcoupled average power for the 7th-order harmonic[Reference Ozawa, Kuwata-Gonokami and Kobayashi24] and was improved to 0.5 mW recently but with limited operation period of time due to the damage of the output coupler[Reference Ozawa, Zhao, Kuwata-Gonokami and Kobayashi13]. As shown in Figure 1, the output from the laser system could be guided to the fsEC either directly or via an external pulse compression stage. In the pulse compression setup, to broaden the spectrum, a 2-cm-long photonic crystal fiber (PCF) (Thorlabs, LMA-35) was employed. The laser was focused into the fiber with a lens (focal length
$f=50~\text{mm}$
). To avoid damages due to self-focusing inside the fiber, a quarter-wave plate (QWP) was inserted before the lens to convert the original linear polarization to a circular one[Reference Smith, Do, Hadley and Farrow25]. The coupling efficiency was
${\sim}85\%$
for input power of 15 W. The transmitted beam was collimated by another lens
$(f=50~\text{mm})$
and the combination of a half-wave plate (HWP) with a QWP changed the polarization state back to the linear one. A pair of transmission gratings, with a groove density of
$1000~\text{lines}/\text{mm}$
, was used to compensate the chirp of output pulses. The pulse duration was characterized by frequency-resolved optical gating (FROG) to be
${\sim}70~\text{fs}$
. Figure 2(a) shows the optical spectra recorded before and after the PCF. The spectrum recorded after the PCF was much broader than the one recorded before. Figure 2(b) shows the pulse shapes of the original
${\sim}200~\text{fs}$
pulse and the compressed one. A combination of half-wave plates and polarizing beam splitter (PBS) was used to filter out the depolarized component. With approximately 15 W of power incident to the LMA fiber, 10 W of output power was obtained after the chirp removal, corresponding to a total efficiency of 67%, as indicated in Figure 2(c). Figure 2(d) shows the beam profile of the compressed beam.
Here we briefly describe the enhancement cavity setup, (for further details see Ref. [Reference Emaury, Diebold, Saraceno and Keller5]). The cavity was a four mirror based bow-tie cavity, as shown in Figure 1. Four mirrors were placed in three separated chambers, which were connected to one another with vacuum-sealed tubes. The driving laser was kept at the resonance of the fsEC by actively adjusting the cavity length of the oscillator. The radius of curvature (ROC) of curved mirrors (M3 and M4) was
$400~\text{mm}$
. The focal radius is estimated to be
${\sim}21~\unicode[STIX]{x03BC}\text{m}$
. To drive the HHG process, Xe, Kr, or Ar gas was introduced at the focus of the cavity by a fused-silica capillary nozzle with an opening diameter of
${\sim}150~\unicode[STIX]{x03BC}\text{m}$
. A gas catcher was used to remove the excess gas inside the cavity. This not only mitigated the load of the turbo-pumps, but also relaxed the potential absorption of the generated high harmonics radiation. The produced high harmonics were separated from the fundamental beam by a Brewster-angled MgO output coupler with dielectric coating, which has high reflectivity (typically
${>}\sim 50\%$
) for the 7th-order harmonic wavelength. The harmonic radiations were guided toward a VUV toroidal grating, and separated beam spots corresponding to the different harmonic orders appeared on the fluorescent plate. By inserting a glass plate of known reflectivity, the harmonic beams could also be directed to a phototube (Hamamatsu R1187) for absolute power measurements. Because of the wavelength dependency of the phototube efficiency and the MgO plate reflectivity, the measured output power was dominated by the 7th-order harmonic radiation.
Table 1. The average power inside the enhancement cavity for short pulse duration
$({\sim}70~\text{fs})$
at different conditions for 1% and 3% IC. IC: input coupler, IP: intra-cavity power, W/O gas: without gas loaded, With gas: with gas loaded.
Figure 3. Long-term measurement of average outcoupled power of 7th order of harmonic with Xe using
${\sim}70~\text{fs}$
driving laser and 3% IC.
The intra-cavity HHG experiments were first carried out using the post-compressed laser pulse and a 1% transmission input coupler (IC). In this case, when there was no gas loaded in, the intra-cavity power was estimated to be
${\sim}0.78~\text{kW}$
(Table 1), which was calculated using the signal transmitted by M3 (shown in Figure 1) and the known transmissivity of M3. Considering the seed power of 9 W, the power enhancement ratio was 87, which was lower than the one reported in Ref. [Reference Ozawa, Zhao, Kuwata-Gonokami and Kobayashi13], in part due to the lower spatial mode-matching between the seed and cavity beams, as well as the broader spectrum. When the noble gas of Xe, Kr, or Ar was introduced, the intra-cavity power decreased to 0.31, 0.47, and 0.53 kW (Table 1), respectively. Under this condition, outcoupled 7th-order harmonic power was measured to be
${\sim}200~\unicode[STIX]{x03BC}\text{W}$
with Xe. However, with 1% transmission IC, the cavity-locking was found to be very sensitive to disturbances, such as nonlinearity of the plasma at the focus, mechanical vibration of the setup and possible phase/amplitude/beam-pointing fluctuations of the externally compressed pulses. An IC with higher transmission decreases the finesse of the cavity and leads to a smaller power enhancement, but a more stable cavity-locking performance. Accordingly, a 3% transmission IC was used in subsequent experiments. The intra-cavity power was estimated to be
${\sim}0.41~\text{kW}$
(Table 1) with 9 W of driving laser power and without gas loaded in, corresponding to a power enhancement ratio of 45. When the noble gas was introduced, the intra-cavity power of 0.28, 0.34, and 0.41 kW (Table 1) was obtained, respectively, for Xe, Kr and Ar gases. Compared with the configuration with the 1% transmission IC, the power loss due to the introduction of the noble gas mitigated significantly for all three gas species. Nearly identical intra-cavity power was obtained for 1% and 3% transmission ICs when Xe gas was used for HHG, despite the differences in cavity finesse. This indicates that power buildup in the cavity with 1% transmission IC was strongly limited by intensity clamping due to plasma nonlinearity effect when Xe gas was used. On this point, intensive investigations have been reported both with numerical simulations and experiments[Reference Holzberger, Lilienfein, Carstens, Saule, Högner, Lücking, Trubetskov, Pervak, Eidam, Limpert, Tünnermann, Fill, Krausz and Pupeza26–Reference Carlson, Lee, Mongelli, Wright and Jones29]. The rapidly growing plasma density within the duration of driving pulses induces time-dependent phase shift which limits the coherent addition of intra-cavity and seeding pulses. The plasma in the cavity introduces a constant round trip phase offset into the cavity, which is found to introduce the instability to the active cavity-locking setup. In addition, spatial effect such as plasma-defocusing also affects the intra-cavity power. Meanwhile, the long-term cavity stability was improved with the 3% transmission IC. Figure 3 is the long-term measurement of the average power of the outcoupled 7th-order harmonic radiation obtained with Xe gas, using the
${\sim}70~\text{fs}$
driving laser and the 3% transmission IC. An outcoupled average power in excess of 0.1 mW could be maintained for over 30 min. The visible fluctuation in Figure 3 was considered to mainly originate from the fluctuation of
$f_{\text{ceo}}$
, which deteriorates the phase coherent addition of seeding pulses and interactivity pulse train. It was often possible to revive the intra-cavity power to its original level by re-adjusting the
$f_{\text{ceo}}$
. In addition to the
$f_{\text{ceo}}$
-drift, the long-term power drift of
${>}15~\text{min}$
scale could also be affected by the degradation of outcoupling plate and misalignment of the cavity. When 3% IC was utilized, the intra-cavity power with Ar gas and empty cavity showed identical intra-cavity power. As will be discussed later, the intensity clamping effect is enhanced with higher finesse cavity, meanwhile we obtained higher peak intensity at focus by using 1% IC rather than 3% IC (
$5.5\times 10^{13}~\text{W}/\text{cm}^{2}$
and
$4.2\times 10^{13}~\text{W}/\text{cm}^{2}$
, respectively, for 1% and 3% ICs). These observations indicate that intensity clamping effect due to plasma nonlinearity was minor when Ar gas was used with 3% transmission IC. This can be explained by rather low seeding power for the fsEC for
${\sim}70~\text{fs}$
pulses case, which did not enable us to reach the intensity level limited by the plasma-nonlinear effect with 3% IC when Ar gas was used for HHG.
It is interesting to compare the results with 70 fs pulses with our previous demonstration of cavity enhanced HHG with 200 fs pulses. With the
${\sim}200~\text{fs}$
pulses and the seed power of 14 W, an intra-cavity power of 0.94 kW was obtained in the absence of gas[Reference Ozawa, Zhao, Kuwata-Gonokami and Kobayashi13]. When Xe gas was introduced for HHG, the power decreased to 0.78 kW. Although the intra-cavity power was significantly lower in the case of the shorter pulses (0.28 kW for
${\sim}70~\text{fs}$
case versus 0.78 kW for
${\sim}200~\text{fs}$
case), the power of the 7th-order harmonic radiation was similar compared with the longer pulse case, and the power was approximately
$200~\unicode[STIX]{x03BC}\text{W}$
for both 70 fs and 200 fs cases. The obtained high harmonics spectra using Xe gas are shown in Figure 4 for
${\sim}70~\text{fs}$
and
${\sim}200~\text{fs}$
pulses, where the wavelength dependence of the diffraction grating efficiency, the luminescent yield of the fluorescent material and reabsorptions by the gases were not taken into account. Harmonics up to the 29th-order
$({\sim}35.9~\text{nm})$
were observed with the
${\sim}70~\text{fs}$
driving laser, while the harmonics beyond 25th is hardly visible in the case of the
${\sim}200~\text{fs}$
driving laser. Experimentally, much stronger plasma could be easily noticed for the case with Xe loaded compared with the cases of Ar and Kr loaded.
Figure 4. Outcoupled high harmonic spectra for post-compressed pulses (red) and original pulses (blue). The pulse durations of those pulses are estimated to be
${\sim}70~\text{fs}$
(red) and
${\sim}200~\text{fs}$
(blue). Xe gas was used. The first row of black dots indicates the position of different harmonic orders from 7th to 39th. For saving space, the numbers of 15th to 37th are now shown here. The second row of black dots indicates the contributions from higher order diffraction.
When the peak intensity at focus increases, significant ionization of the gas medium introduces loss and phase shift to the intra-cavity pulses, which clamps the available peak intensity at the focus[Reference Holzberger, Lilienfein, Carstens, Saule, Högner, Lücking, Trubetskov, Pervak, Eidam, Limpert, Tünnermann, Fill, Krausz and Pupeza26]. Shorter pulses and lower finesse of the cavity are advantageous to achieve higher clamping intensity. Based on the empirical expression given in Ref. [Reference Holzberger, Lilienfein, Carstens, Saule, Högner, Lücking, Trubetskov, Pervak, Eidam, Limpert, Tünnermann, Fill, Krausz and Pupeza26], 15% to 20% higher peak intensity can be expected using
${\sim}70~\text{fs}$
instead of
${\sim}200~\text{fs}$
pulse. The observed improvements in conversion efficiency for 7th harmonic radiation and a little extended cut-off of harmonic orders can be ascribed to this effect.
As discussed above, the intensity clamping effect due to plasma nonlinearity was minor when Ar gas was used with 3% transmission IC. If the cavity is seeded with higher average power for
${\sim}70~\text{fs}$
pulses until intra-cavity power being clamped by plasma nonlinearity, significant improvement in intra-cavity peak intensity and thus in harmonic orders could be expected.
For obtaining higher power from the post-compression stages, the chirp of the incident laser could be adjusted to provide a longer pulse duration and the incident power could be increased to avoid the peak power being limited by self-focusing effects. Higher seeding powers and shorter pulse durations can tolerate the use of highly transmissive ICs, while keeping the peak intensity sufficiently elevated for HHG limited by nonlinear response of cavity with gas medium.
3 Conclusion
In conclusion, a nonlinear compression stage was introduced to an Yb-FCPA laser to shorten the pulse duration and efficiently drive the intra-cavity HHG process. The system was designed such that short and long pulse operation could be switched from one to the other, making the configuration versatile and applicable to measurements requiring both high temporal and spectral resolutions. We found that applying nonlinear compression stage gives higher HHG efficiency due to less phase distortion caused by the plasma nonlinearity. In addition, a 3% transmission IC was adopted to improve the locking stability of the fsEC. Stable operation was demonstrated for over 30 min and with an average power in excess of 0.1 mW. Along with the sub-100 fs NIR laser, short pulsed 7th-order harmonic radiation should enable to carry out time-resolved coincidence experiments at high repetition rates and time-resolved photoelectron spectroscopy.
Acknowledgements
The authors would like to thank Dr. Alissa Silva, from National Physical Laboratory in England, for her careful proof reading, and Dr. Yukiaki Ishida, from the University of Tokyo, for his helpful discussions. This research project was carried out in support of the Photon Frontier Network Program of the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan.
Open access
