The development of the ultrafast laser system opened up a large number of new research fields. New optical techniques have been developed to reduce the pulse duration to a few femtoseconds and/or to increase the peak power to the multi-petawatt range. The generation of ultrashort pulses implies a large bandwidth, increasing complexity of the beam propagation, and diagnostics to fully characterize the final pulse in the spatiotemporal domain. One of the spatiotemporal couplings (STCs)[1] playing a key role in a wide range of scientific areas, e.g., laser development, laser–matter interaction, is the angular dispersion (AD) of the beam. The presence of this chromatic aberration distorts the laser pulse, causing pulse front tilt (PFT)[2]. In turn, when the beam is focused, the actual pulse length in the focal spot is different from the pulse length in the near field, where it is usually measured.
The presence of PFT in the near field has been proved to have an effect on electron acceleration experiments[Reference Thévenet, Mittelberger, Nakamura, Lehe, Schroeder, Vay, Esarey and Leemans3], so its control and measurement are important for the development of compact laser-driven plasma accelerators and, more generally, to guarantee the best performance of high-power laser facilities.
In high-power ultrashort laser systems, slight misalignment of the compressor and/or the stretcher can generate AD[Reference Osvay, Kovacs, Heiner, Kurdi, Klebniczki and Csatari4]. Different diagnostics[Reference Jolly, Gobert and Quéré5] have been proposed to characterize these aberrations, based on interferometric[Reference Sharma, Patidar, Raghuramaiah, Naik and Gupta6, Reference Li, Miyanaga and Kawanaka7], spectral–temporal[Reference Gallmann, Steinmeyer, Sutter, Rupp, Iaconis, Walmsley and Keller8], autocorrelation[Reference Figueira, Braga, Ahmed, Boyle, Galimberti, Galletti and Oliveira9], chromatic[Reference Bahk, Dorrer and Bromage10] or wave-front distortion[Reference Li and Kawanaka11] techniques. Unfortunately, these diagnostics involve complex setup[Reference Li and Kawanaka12–Reference Jean-Baptiste, Zhao, Rodrigo and Thomas14], originating from complex alignment procedures, and most of them are self-referenced[Reference Akturk, Kimmel, O’Shea and Trebino15], so they need a good-quality beam, both in the spatial and the temporal domains. Moreover, they involve complex retrieval routines, sometimes leading to ambiguities in the detection of STCs[Reference Li, Miyanaga and Kawanaka7] or providing only qualitative measurements.
In this Letter, we propose a simple innovative single-shot method, based on an intensity mask. It is suitable for characterizing not only short pulses, as required for many available diagnostics, but also stretched pulses. The proposed instrument addresses most of the main issues of existing STC diagnostics: it is a simple retrieval routine able to retrieve different STCs without ambiguities; the simple experimental setup involves simple alignment procedures and the instrument is not a self-referenced method so it does not require a good-quality beam in the spatiotemporal domain. Above all, the main advantage of this new diagnostic is the simplicity of the setup and the ability to show, directly from the acquired image, the presence of PFT prior to the analysis in both directions. The theoretical background and the diagnostic performances are first presented together with simulations, in detail. Second, experimental results, supported by the theoretical analysis of the beam propagation, are reported, confirming the feasibility of our tool.
The basic idea of the proposed instrument is to use a diffraction element to disperse the spectral components angularly. If a transmission grating is used as the diffraction element in the horizontal direction, by focusing the diffraction order and analyzing the diffracted spot, the spectral components are diffracted at different horizontal positions while the vertical position encodes information about the AD. By using a 2D diffraction element and analyzing the diffraction orders in both directions, the AD in both directions can be retrieved. To study in detail the theory behind the instrument, let us consider a low aberrated laser beam that can be described by an electric field ![]() $E\left(r,\lambda \right)$ and an intensity profile
$E\left(r,\lambda \right)$ and an intensity profile ![]() $I\left({r},\lambda \right)$ independent of the wavelength
$I\left({r},\lambda \right)$ independent of the wavelength ![]() $\lambda$, i.e.,
$\lambda$, i.e.,
where ![]() ${r}=\left(x,y\right)$ determines the spatial coordinates in the x–y plane. In the proposed study, the beam polarization is not relevant; thus the electric field is considered to be a scalar quantity.
${r}=\left(x,y\right)$ determines the spatial coordinates in the x–y plane. In the proposed study, the beam polarization is not relevant; thus the electric field is considered to be a scalar quantity.
In the paraxial approximation, adopting an achromatic lens of focal length ![]() $f$, the far-field spectral intensity
$f$, the far-field spectral intensity ![]() $S\left({r},\lambda \right)$ is given by
$S\left({r},\lambda \right)$ is given by
 \begin{align}S\left({r},\lambda \right)=\frac{1}{\lambda^2{f}^2}{\left|\int E\left(\rho, \lambda \right)\kern0.1em \exp \left(-i\kern0.1em \frac{2\pi }{\lambda f}{r}\cdot \rho \right)\mathrm{d}\rho \right|}^2,\end{align}
\begin{align}S\left({r},\lambda \right)=\frac{1}{\lambda^2{f}^2}{\left|\int E\left(\rho, \lambda \right)\kern0.1em \exp \left(-i\kern0.1em \frac{2\pi }{\lambda f}{r}\cdot \rho \right)\mathrm{d}\rho \right|}^2,\end{align}where ![]() ${r}$ and
${r}$ and ![]() $\rho$ are, respectively, the spatial coordinates in the far field and in the near field. Here
$\rho$ are, respectively, the spatial coordinates in the far field and in the near field. Here ![]() $E\left(\rho, \lambda \right)$ is described by
$E\left(\rho, \lambda \right)$ is described by
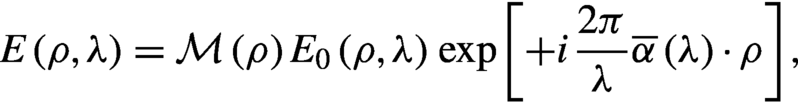 \begin{align}E\left(\rho, \lambda \right)=\mathrm{\mathcal{M}}\left(\rho \right){E}_0\left(\rho, \lambda \right)\kern0.1em \exp \left[+i\kern0.1em \frac{2\pi }{\lambda}\overline{\alpha}\left(\lambda \right)\cdot \rho \right],\end{align}
\begin{align}E\left(\rho, \lambda \right)=\mathrm{\mathcal{M}}\left(\rho \right){E}_0\left(\rho, \lambda \right)\kern0.1em \exp \left[+i\kern0.1em \frac{2\pi }{\lambda}\overline{\alpha}\left(\lambda \right)\cdot \rho \right],\end{align}where ![]() $\overline{\alpha}\left(\lambda \right)$ is the pointing direction for each wavelength
$\overline{\alpha}\left(\lambda \right)$ is the pointing direction for each wavelength ![]() $\lambda$ and
$\lambda$ and ![]() $\mathrm{\mathcal{M}}\left(\rho \right)={\sum}_i\chi \left(\rho - di\right)$ is the periodic amplitude mask where
$\mathrm{\mathcal{M}}\left(\rho \right)={\sum}_i\chi \left(\rho - di\right)$ is the periodic amplitude mask where ![]() $\chi$ is the function describing the mask profile and
$\chi$ is the function describing the mask profile and ![]() $d$ its periodicity. From Equations (1) and (2), the far-field spectral intensity
$d$ its periodicity. From Equations (1) and (2), the far-field spectral intensity ![]() $S\left({r},\lambda \right)$ becomes
$S\left({r},\lambda \right)$ becomes
 \begin{align}S\left({r},\lambda \right)=\sum\limits_n{\mathcal{G}}_{{n}}\kern0.1em {S}_0\kern0em \left[{r}-f\overline{\alpha}\left(\lambda \right)-\frac{\lambda f}{d}{n},\lambda \right],\end{align}
\begin{align}S\left({r},\lambda \right)=\sum\limits_n{\mathcal{G}}_{{n}}\kern0.1em {S}_0\kern0em \left[{r}-f\overline{\alpha}\left(\lambda \right)-\frac{\lambda f}{d}{n},\lambda \right],\end{align}where ![]() ${n}$ is a vector of integers representing the order of diffraction generated by the mask,
${n}$ is a vector of integers representing the order of diffraction generated by the mask, ![]() ${\mathcal{G}}_{{n}}$ is the amplitude factor for each order and
${\mathcal{G}}_{{n}}$ is the amplitude factor for each order and ![]() ${S}_0\left({r},\lambda \right)$ is the spectral intensity profile of the unperturbed far field. Apart from the central spot (
${S}_0\left({r},\lambda \right)$ is the spectral intensity profile of the unperturbed far field. Apart from the central spot (![]() ${n}=\left(0,0\right)$), which represents the unperturbed beam, the spots are spatially dispersed by the grating effect of the intensity mask. Let us now consider a Gaussian beam described by
${n}=\left(0,0\right)$), which represents the unperturbed beam, the spots are spatially dispersed by the grating effect of the intensity mask. Let us now consider a Gaussian beam described by
 \begin{align}{S}_0\left({r},\lambda \right)={I}_0\exp \left[-\frac{1}{2}\frac{{\left|{r}\right|}^2}{\sigma^2}-\frac{1}{2}{\left(\frac{\lambda -{\lambda}_0}{\varDelta}\right)}^2\right].\end{align}
\begin{align}{S}_0\left({r},\lambda \right)={I}_0\exp \left[-\frac{1}{2}\frac{{\left|{r}\right|}^2}{\sigma^2}-\frac{1}{2}{\left(\frac{\lambda -{\lambda}_0}{\varDelta}\right)}^2\right].\end{align}where ![]() $\sigma$ is related to the spot size,
$\sigma$ is related to the spot size, ![]() ${\lambda}_0$ is the laser central wavelength and
${\lambda}_0$ is the laser central wavelength and ![]() $\varDelta$ is related to the pulse bandwidth. Assuming a linear and relatively small AD (respectively,
$\varDelta$ is related to the pulse bandwidth. Assuming a linear and relatively small AD (respectively, ![]() $\overline{\alpha}\left(\lambda \right)=\alpha \left(\lambda -{\lambda}_0\right)$ and
$\overline{\alpha}\left(\lambda \right)=\alpha \left(\lambda -{\lambda}_0\right)$ and ![]() $\mid \alpha \mid \ll 1/d$) and just the first diffraction order (
$\mid \alpha \mid \ll 1/d$) and just the first diffraction order (![]() $\mid {n}\mid =1$), the intensity profile
$\mid {n}\mid =1$), the intensity profile ![]() ${I}_x^{\pm }$ of the diffraction order
${I}_x^{\pm }$ of the diffraction order ![]() ${n}=\left(\pm 1,0\right)$ is
${n}=\left(\pm 1,0\right)$ is
 \begin{align}{I}_x^{\pm}\left(x,y\right)\propto \exp \left\{-\frac{1}{2}\left\{{\left(\frac{x-{x}_{\pm }}{\varOmega_x^{\pm }}\right)}^2+{\left[\frac{y-{A}_x^{\pm}\left(x-{x}_{\pm}\right)}{\sigma}\right]}^2\right\}\right\},\end{align}
\begin{align}{I}_x^{\pm}\left(x,y\right)\propto \exp \left\{-\frac{1}{2}\left\{{\left(\frac{x-{x}_{\pm }}{\varOmega_x^{\pm }}\right)}^2+{\left[\frac{y-{A}_x^{\pm}\left(x-{x}_{\pm}\right)}{\sigma}\right]}^2\right\}\right\},\end{align}where
 \begin{align}{\varOmega}_x^{\pm }=\frac{f\varDelta}{d}\sqrt{\varGamma \pm 2d{\alpha}_x},\enspace {A}_x^{\pm }&=\pm {\left(\varGamma \pm 2d{\alpha}_x\right)}^{-1}d{\alpha}_y,\notag\\{}{x}_{\pm }=\pm \frac{f{\lambda}_0}{d},\enspace \varGamma &=1+{\left(\frac{d\sigma}{\varDelta f}\right)}^2.\end{align}
\begin{align}{\varOmega}_x^{\pm }=\frac{f\varDelta}{d}\sqrt{\varGamma \pm 2d{\alpha}_x},\enspace {A}_x^{\pm }&=\pm {\left(\varGamma \pm 2d{\alpha}_x\right)}^{-1}d{\alpha}_y,\notag\\{}{x}_{\pm }=\pm \frac{f{\lambda}_0}{d},\enspace \varGamma &=1+{\left(\frac{d\sigma}{\varDelta f}\right)}^2.\end{align}Equations (5) and (6) are also valid for the y-coordinate by just replacing x with y. The AD ![]() $\alpha$ can be obtained by solving the linear system
$\alpha$ can be obtained by solving the linear system
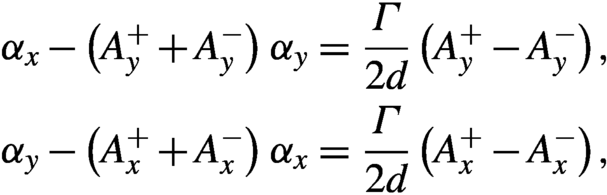 \begin{align}{\alpha}_x-\left({A}_y^{+}+{A}_y^{-}\right)\kern0.1em {\alpha}_y& = \frac{\varGamma }{2d}\left({A}_y^{+}-{A}_y^{-}\right),\notag\\{}{\alpha}_y-\left({A}_x^{+}+{A}_x^{-}\right)\kern0.1em {\alpha}_x& = \frac{\varGamma }{2d}\left({A}_x^{+}-{A}_x^{-}\right),\end{align}
\begin{align}{\alpha}_x-\left({A}_y^{+}+{A}_y^{-}\right)\kern0.1em {\alpha}_y& = \frac{\varGamma }{2d}\left({A}_y^{+}-{A}_y^{-}\right),\notag\\{}{\alpha}_y-\left({A}_x^{+}+{A}_x^{-}\right)\kern0.1em {\alpha}_x& = \frac{\varGamma }{2d}\left({A}_x^{+}-{A}_x^{-}\right),\end{align}while the scaling factor ![]() $\varGamma$ can be obtained from
$\varGamma$ can be obtained from ![]() ${\varOmega}_x^{\pm }$ and
${\varOmega}_x^{\pm }$ and ![]() $\sigma$ by
$\sigma$ by
 \begin{align}\varGamma =1+{\left[1-\frac{{\left({\varOmega}_x^{+}\right)}^2+{\left({\varOmega}_x^{-}\right)}^2}{2{\sigma}^2}\right]}^{-1}.\end{align}
\begin{align}\varGamma =1+{\left[1-\frac{{\left({\varOmega}_x^{+}\right)}^2+{\left({\varOmega}_x^{-}\right)}^2}{2{\sigma}^2}\right]}^{-1}.\end{align}Starting from the image and considering only the diffraction order ![]() ${n}=\left(+1,0\right)$, the parameters
${n}=\left(+1,0\right)$, the parameters ![]() ${A}_x^{+}$,
${A}_x^{+}$, ![]() ${\varOmega}_x^{+}$ and
${\varOmega}_x^{+}$ and ![]() $\sigma$ can be retrieved by analyzing the diffracted spot. With a fixed position on the x-axis, the barycenter
$\sigma$ can be retrieved by analyzing the diffracted spot. With a fixed position on the x-axis, the barycenter ![]() ${y}_{\rm B}$ and the root mean square deviation (RMSD)
${y}_{\rm B}$ and the root mean square deviation (RMSD) ![]() ${\sigma}_{\rm B}$ are calculated along the y-axis. The average of
${\sigma}_{\rm B}$ are calculated along the y-axis. The average of ![]() ${\sigma}_{\rm B}$ provides the estimation for
${\sigma}_{\rm B}$ provides the estimation for ![]() $\sigma$, while the RMSD value along the x-axis, after integrating along the y-axis, gives an estimation of
$\sigma$, while the RMSD value along the x-axis, after integrating along the y-axis, gives an estimation of ![]() ${\varOmega}_x^{+}$. A linear regression of
${\varOmega}_x^{+}$. A linear regression of ![]() ${y}_{\rm B}$ retrieves the slope
${y}_{\rm B}$ retrieves the slope ![]() ${A}_x^{+}$ (Figure 1).
${A}_x^{+}$ (Figure 1).
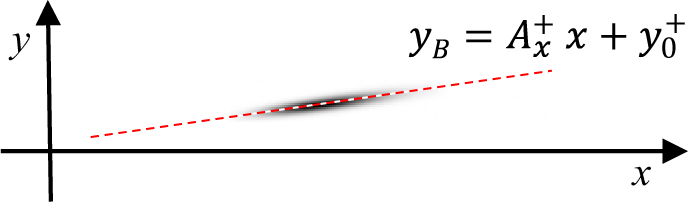
Figure 1 Simulated image of the first diffracted spot (![]() ${n}=\left(+1,0\right)$) in x with the linear regression to retrieve the slope
${n}=\left(+1,0\right)$) in x with the linear regression to retrieve the slope ![]() ${A}_x^{+}$.
${A}_x^{+}$.
The focal length of the lens has a direct implication for the resolution of the instrument: a longer focal length creates a larger deviation, encoding the information on a larger number of pixels. However, it also requires a larger camera sensor to be able to collect the first orders of diffraction. So, with the parameters of the camera (number of pixels ![]() $\mathcal{N}$ and pixel size
$\mathcal{N}$ and pixel size ![]() ${\sigma}_{\rm pxl}$) and the period of the mask (
${\sigma}_{\rm pxl}$) and the period of the mask (![]() $d$) fixed, the optimal focal length
$d$) fixed, the optimal focal length ![]() ${f}_{\rm opt}$ should be chosen to maximize the separation of the first orders, avoiding clipping at the edge of the bandwidth, i.e.,
${f}_{\rm opt}$ should be chosen to maximize the separation of the first orders, avoiding clipping at the edge of the bandwidth, i.e.,
 \begin{align}{f}_{\rm opt}\approx \frac{\mathcal{N}{\sigma}_{\rm pxl}d}{2\left({\lambda}_0+\varDelta \right)}.\end{align}
\begin{align}{f}_{\rm opt}\approx \frac{\mathcal{N}{\sigma}_{\rm pxl}d}{2\left({\lambda}_0+\varDelta \right)}.\end{align}From the AD values ![]() $\alpha$, it is easy to obtain the PFT and PFT angles
$\alpha$, it is easy to obtain the PFT and PFT angles ![]() $\zeta$ in the near field:
$\zeta$ in the near field:

where c is the speed of light in a vacuum.
To validate the instrument, a software program was developed to simulate the focusing of a broad-bandwidth laser beam. The program takes an arbitrary shape of the input beam in the spectrum-space domain and simulates the focusing described by Equation (1). For each wavelength, a numerical Fourier transform is performed, obtaining the simulated focal spot images. Each image is then re-scaled to the same resolution and integration over the wavelength range is performed to obtain the final focal spot image. The program is implemented using the ArrayFire library[Reference Yalamanchili, Arshad, Mohammed, Garigipati, Entschev, Kloppenborg, Malcolm and Melonakos16] and the CUDA library and it was run on a PC with an NVIDIA M6000 graphics card. All the simulations were performed using a 2048×2048 point array with a pixel size of 5.3 μm and 64 samplings in the spectral domain. The camera had a resolution of ![]() $1024\times 1024$ pixels, a squared mask of 100 μm with a periodicity of d = 156 μm (commercially available) and a lens with a focal length of f = 300 mm. These parameters were chosen to match both the camera and the amplitude mask used in the experimental validation, presented below. To generate more realistic images, some white noise was added and digitization to 8-bit dynamics was considered. Figure 2 shows a simulated image for a Gaussian beam, similar to that in the experimental case, of 7.65 mm full width at half maximum (FWHM), with a Gaussian spectrum having a central wavelength
$1024\times 1024$ pixels, a squared mask of 100 μm with a periodicity of d = 156 μm (commercially available) and a lens with a focal length of f = 300 mm. These parameters were chosen to match both the camera and the amplitude mask used in the experimental validation, presented below. To generate more realistic images, some white noise was added and digitization to 8-bit dynamics was considered. Figure 2 shows a simulated image for a Gaussian beam, similar to that in the experimental case, of 7.65 mm full width at half maximum (FWHM), with a Gaussian spectrum having a central wavelength ![]() ${\lambda}_0=800\;\mathrm{nm}$,
${\lambda}_0=800\;\mathrm{nm}$, ![]() $25\;\mathrm{nm}$ FWHM bandwidth and AD of
$25\;\mathrm{nm}$ FWHM bandwidth and AD of ![]() $\alpha =\left(\mathrm{11.5,0}\right)\;\mathrm{\mu} \mathrm{rad}/\mathrm{nm}$. The intensity level was chosen to maximize the dynamics on the first-order diffracted spots, clearly visible in the image.
$\alpha =\left(\mathrm{11.5,0}\right)\;\mathrm{\mu} \mathrm{rad}/\mathrm{nm}$. The intensity level was chosen to maximize the dynamics on the first-order diffracted spots, clearly visible in the image.
Starting from the image (simulated or experimental) of the focal plane (Figure 2), a background subtraction algorithm and numerical filtering were performed. The resulting image was centred and each diffracted spot was analyzed to obtain the parameters ![]() ${A}_x^{\pm }$,
${A}_x^{\pm }$,  ${A}_y^{\pm }$,
${A}_y^{\pm }$, ![]() ${\varOmega}_x^{\pm }$,
${\varOmega}_x^{\pm }$,  ${\varOmega}_y^{\pm }$ and
${\varOmega}_y^{\pm }$ and ![]() $\sigma$, as defined in Equation (6). Using Equation (8) to estimate
$\sigma$, as defined in Equation (6). Using Equation (8) to estimate ![]() $\varGamma$ and solving the system of Equation (7), we obtained the retrieved AD values
$\varGamma$ and solving the system of Equation (7), we obtained the retrieved AD values ![]() ${\alpha}^{\rm R}$. The estimation of the error on the retrieved AD was performed by taking the noise level of the image and using the error propagation theory.
${\alpha}^{\rm R}$. The estimation of the error on the retrieved AD was performed by taking the noise level of the image and using the error propagation theory.
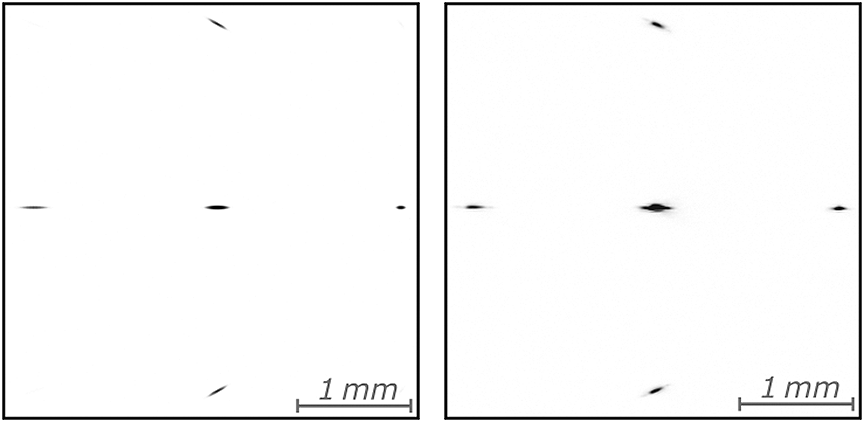
Figure 2 Camera image comparison for a ![]() $7.65\;\mathrm{mm}$ FWHM Gaussian beam with
$7.65\;\mathrm{mm}$ FWHM Gaussian beam with ![]() $25\kern0.1em nm$ FWHM Gaussian spectrum around
$25\kern0.1em nm$ FWHM Gaussian spectrum around ![]() $800\;\mathrm{nm}$ and AD of
$800\;\mathrm{nm}$ and AD of ![]() $\alpha =\left(\mathrm{11.5,0}\right)\kern0.1em \mu \hbox{rad}/\hbox{nm}$: (left) simulated image; (right) experimental image.
$\alpha =\left(\mathrm{11.5,0}\right)\kern0.1em \mu \hbox{rad}/\hbox{nm}$: (left) simulated image; (right) experimental image.
A set of images, having different amplitude of AD values as ![]() $\alpha =\left(t/d\cos \theta, t/d\sin \theta \right)$ where
$\alpha =\left(t/d\cos \theta, t/d\sin \theta \right)$ where ![]() $t/d$ is the AD modulus and
$t/d$ is the AD modulus and ![]() $\theta$ the direction, was used to numerically test the instrument. The simulated beam was a Gaussian beam of
$\theta$ the direction, was used to numerically test the instrument. The simulated beam was a Gaussian beam of ![]() $5\ \hbox{mm}$ FWHM and had a Gaussian spectrum with a central wavelength of
$5\ \hbox{mm}$ FWHM and had a Gaussian spectrum with a central wavelength of ![]() ${\lambda}_0=800\ \hbox{nm}$ and a bandwidth of
${\lambda}_0=800\ \hbox{nm}$ and a bandwidth of ![]() $50\ \hbox{nm}$ FWHM. The plot of the retrieved
$50\ \hbox{nm}$ FWHM. The plot of the retrieved ![]() ${\alpha}_x^{\rm R}$ and
${\alpha}_x^{\rm R}$ and ![]() ${\alpha}_y^{\rm R}$ versus the simulated
${\alpha}_y^{\rm R}$ versus the simulated ![]() ${\alpha}_x$ and
${\alpha}_x$ and ![]() ${\alpha}_y$ AD values is shown in Figure 3. The plot shows a clear agreement between the simulated and the retrieved values for a small value of
${\alpha}_y$ AD values is shown in Figure 3. The plot shows a clear agreement between the simulated and the retrieved values for a small value of ![]() $\mid \alpha \mid$, where the condition
$\mid \alpha \mid$, where the condition
is fulfilled. In more detail, the induced error is ![]() $0.018\ \mu \hbox{rad/nm}$ for
$0.018\ \mu \hbox{rad/nm}$ for ![]() $\mid \alpha \mid =0.2/d$ and
$\mid \alpha \mid =0.2/d$ and ![]() $0.041\ \mu\,\hbox{rad/nm}$ for
$0.041\ \mu\,\hbox{rad/nm}$ for ![]() $\mid \alpha \mid =0.3/d$, compared with the estimated measurement error of
$\mid \alpha \mid =0.3/d$, compared with the estimated measurement error of ![]() $0.033\ \mu\hbox{rad/nm}$ for both cases. At larger AD amplitude, there is poor agreement between the retrieved and the simulated AD, except when the AD is in the diffraction direction of the intensity mask, i.e.,
$0.033\ \mu\hbox{rad/nm}$ for both cases. At larger AD amplitude, there is poor agreement between the retrieved and the simulated AD, except when the AD is in the diffraction direction of the intensity mask, i.e., ![]() $\theta =0$,
$\theta =0$, ![]() $\theta =\pi$ or
$\theta =\pi$ or ![]() $\theta =\pm \pi$, where the induced error is of the order of
$\theta =\pm \pi$, where the induced error is of the order of ![]() $0.033\ \mu\hbox{rad/nm}$. In this case, the maximum measurable amplitude of the AD is limited only by the dimension of the camera, which can cause clipping on the diffracted spots, and superimposition between the first and the second diffraction orders. To fully test the instrument, different beam parameters were simulated using the AD of
$0.033\ \mu\hbox{rad/nm}$. In this case, the maximum measurable amplitude of the AD is limited only by the dimension of the camera, which can cause clipping on the diffracted spots, and superimposition between the first and the second diffraction orders. To fully test the instrument, different beam parameters were simulated using the AD of  $\left|\alpha \right|=\frac{0.2}{d}\simeq 1.28\;\mathrm{\mu} \mathrm{rad}/\mathrm{nm}$ and different
$\left|\alpha \right|=\frac{0.2}{d}\simeq 1.28\;\mathrm{\mu} \mathrm{rad}/\mathrm{nm}$ and different ![]() $\theta$, keeping the same parameters as in the previous simulations. The retrieved AD
$\theta$, keeping the same parameters as in the previous simulations. The retrieved AD ![]() ${\alpha}^{\rm R}$ was analyzed, performing a linear fit, namely
${\alpha}^{\rm R}$ was analyzed, performing a linear fit, namely
 $$\begin{align*}{\alpha}_{x,y}^{\rm R}=\eta \kern0.1em {\alpha}_{x,y},\end{align*}$$
$$\begin{align*}{\alpha}_{x,y}^{\rm R}=\eta \kern0.1em {\alpha}_{x,y},\end{align*}$$extracting the systematic calibration error ![]() $\eta$ and standard deviation of the residual
$\eta$ and standard deviation of the residual ![]() ${\sigma}_{\rm err}$. Varying the shape of the spectrum from Gaussian to flat-top, no substantial influence on the retrieved AD is noticed, as shown in Table 1. On the other hand, the spatial shaping of the beam in the near field (from Gaussian to square flat-top) caused the retrieved AD to be underestimated by
${\sigma}_{\rm err}$. Varying the shape of the spectrum from Gaussian to flat-top, no substantial influence on the retrieved AD is noticed, as shown in Table 1. On the other hand, the spatial shaping of the beam in the near field (from Gaussian to square flat-top) caused the retrieved AD to be underestimated by ![]() $\sim$15%. The near-field beam size has a marginal influence, while the decrease of the spectral bandwidth below
$\sim$15%. The near-field beam size has a marginal influence, while the decrease of the spectral bandwidth below ![]() $\approx 25\kern0.1em \hbox{nm}$ affects the retrieval, where the retrieved error increases with the reduction of the bandwidth (Figure 4). The proposed technique, in its current status, cannot manage the overlapping of the second order with the first order of diffraction. A possible workaround is to insert a known AD at
$\approx 25\kern0.1em \hbox{nm}$ affects the retrieval, where the retrieved error increases with the reduction of the bandwidth (Figure 4). The proposed technique, in its current status, cannot manage the overlapping of the second order with the first order of diffraction. A possible workaround is to insert a known AD at ![]() ${45}^{\circ }$ from the diffraction direction by a prism, to separate the dispersion orders. The analysis routine could be easily modified to take into account the additional AD.
${45}^{\circ }$ from the diffraction direction by a prism, to separate the dispersion orders. The analysis routine could be easily modified to take into account the additional AD.

Figure 3 Retrieved versus simulated AD for a 50 nm FWHM Gaussian spectrum and 5 mm FWHM Gaussian beam for a different AD modulus.
Table 1 Influence of the beam and spectral shape.
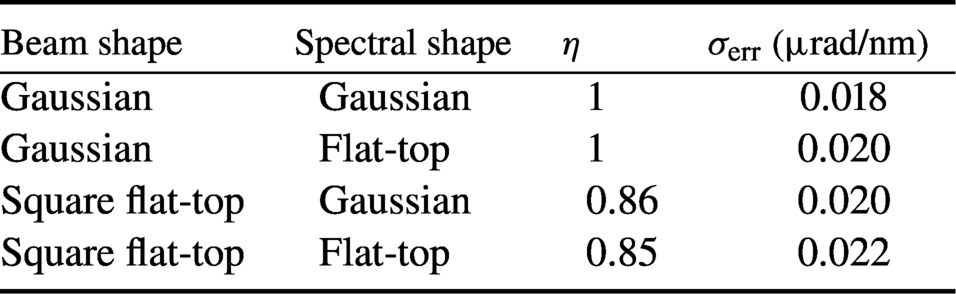
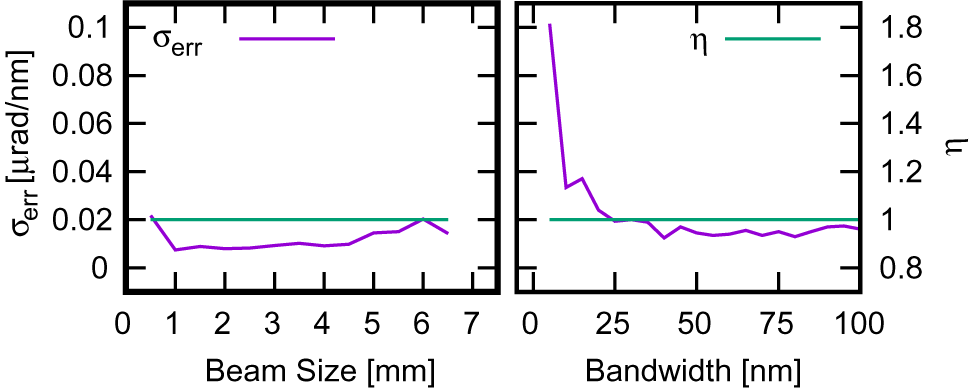
Figure 4 Influence on calibration ![]() $\eta$ and retrieved error
$\eta$ and retrieved error ![]() ${\sigma}_{\rm err}$ of various beam parameters: (left) beam size FWHM; (right) spectral bandwidth FWHM.
${\sigma}_{\rm err}$ of various beam parameters: (left) beam size FWHM; (right) spectral bandwidth FWHM.
The presence of astigmatism is well tolerated if small (![]() $<0.2\kern0.1em {\lambda}_0$ of peak-to-valley aberration), while for higher values it largely degrades the retrieved error. Also, the calibration error
$<0.2\kern0.1em {\lambda}_0$ of peak-to-valley aberration), while for higher values it largely degrades the retrieved error. Also, the calibration error ![]() $\eta$ became significantly different from 1 for aberration greater than
$\eta$ became significantly different from 1 for aberration greater than ![]() $0.3\kern0.1em {\lambda}_0$ (Figure 5 (left)). It should be emphasized that, for each aberration value, the angular direction of the astigmatism was chosen randomly. Finally, the chromatic defocusing is well tolerated by the instrument, with a modest increase of the retrieved error with increase of the aberration (Figure 5 (right)). The instrument was validated experimentally with the FLAME laser[Reference Bisesto, Anania, Bellaveglia, Chiadroni, Cianchi, Costa, Curcio, Di Giovenale, Di Pirro, Ferrario, Filippia, Galloa, Marocchinoa, Pompilia, Ziglerad and Vaccarezzaa17], exploiting the auxiliary beamline usually used as probe beam[Reference Galletti, Coyle, Oliveira, Galimberti, Bisesto and Giulietti18]. Figure 6 shows a schematic of the experimental setup. A Ti:sapphire laser delivers tens of femtoseconds, nanojoule-level, 800 nm pulses at 80 MHz. Its output is stretched to
$0.3\kern0.1em {\lambda}_0$ (Figure 5 (left)). It should be emphasized that, for each aberration value, the angular direction of the astigmatism was chosen randomly. Finally, the chromatic defocusing is well tolerated by the instrument, with a modest increase of the retrieved error with increase of the aberration (Figure 5 (right)). The instrument was validated experimentally with the FLAME laser[Reference Bisesto, Anania, Bellaveglia, Chiadroni, Cianchi, Costa, Curcio, Di Giovenale, Di Pirro, Ferrario, Filippia, Galloa, Marocchinoa, Pompilia, Ziglerad and Vaccarezzaa17], exploiting the auxiliary beamline usually used as probe beam[Reference Galletti, Coyle, Oliveira, Galimberti, Bisesto and Giulietti18]. Figure 6 shows a schematic of the experimental setup. A Ti:sapphire laser delivers tens of femtoseconds, nanojoule-level, 800 nm pulses at 80 MHz. Its output is stretched to ![]() $\sim 100\;\mathrm{ps}$ in a double-pass stretcher. Subsequently, the pulses are amplified, reaching 50 mJ energy level at 10 Hz (Amplifier). The laser output (70 fs, 25 nm bandwidth centered at 800 nm,
$\sim 100\;\mathrm{ps}$ in a double-pass stretcher. Subsequently, the pulses are amplified, reaching 50 mJ energy level at 10 Hz (Amplifier). The laser output (70 fs, 25 nm bandwidth centered at 800 nm, ![]() $\sim 10\;\mathrm{mJ}$,
$\sim 10\;\mathrm{mJ}$, ![]() $\sim 13\ \mathrm{mm}\ 1/{e}^2$ diameter), coming from the optical double-pass two-grating femtosecond compressor (Compressor), is split into two arms by a beam splitter (BS). The reflected beam is redirected, thanks to a simple reflective optic , onto a diffractive mask (MK) with a periodicity d of 156 μm and then focused onto a CCD by means of a 300 mm focal length achromatic doublet (L). Simultaneously, the transmitted beam is sent into an APE Compact LX-SPIDER[19] for complete characterization in the spectral–temporal domain (phase retrieval and temporal measurement). Data from both instruments are collected by a computer, allowing a complete pulse characterization for each shot. The compressor parallelism was modified, moving the second grating (second and third passes) on the dispersion plane by a calibrated angle
$\sim 13\ \mathrm{mm}\ 1/{e}^2$ diameter), coming from the optical double-pass two-grating femtosecond compressor (Compressor), is split into two arms by a beam splitter (BS). The reflected beam is redirected, thanks to a simple reflective optic , onto a diffractive mask (MK) with a periodicity d of 156 μm and then focused onto a CCD by means of a 300 mm focal length achromatic doublet (L). Simultaneously, the transmitted beam is sent into an APE Compact LX-SPIDER[19] for complete characterization in the spectral–temporal domain (phase retrieval and temporal measurement). Data from both instruments are collected by a computer, allowing a complete pulse characterization for each shot. The compressor parallelism was modified, moving the second grating (second and third passes) on the dispersion plane by a calibrated angle ![]() $\delta \theta$ to introduce a controlled AD, in the well-known
$\delta \theta$ to introduce a controlled AD, in the well-known ![]() $4\times 4$ Kostenbauder formalism, given by
$4\times 4$ Kostenbauder formalism, given by
 $$\begin{align*}\hbox{PFT}=\frac{2{\lambda}_0\kern0.1em \tan {\theta}_{\rm d}}{c\kern0.1em d\kern0.1em \cos {\theta}_{\rm i}}\,\delta \theta, \end{align*}$$
$$\begin{align*}\hbox{PFT}=\frac{2{\lambda}_0\kern0.1em \tan {\theta}_{\rm d}}{c\kern0.1em d\kern0.1em \cos {\theta}_{\rm i}}\,\delta \theta, \end{align*}$$where d is the groove distance, ![]() $c$ is the speed of light and
$c$ is the speed of light and ![]() ${\theta}_{\rm i,d}$ are the incident and diffracted angle, respectively. It should be emphasized that the stretcher is not re-tuned at each induced
${\theta}_{\rm i,d}$ are the incident and diffracted angle, respectively. It should be emphasized that the stretcher is not re-tuned at each induced ![]() $\delta \theta$ so the beam is not always maintained as short as 70 fs but varies from 70 fs to 495 fs. Figure 7 shows the retrieved angular dispersion ADexp. The data were compared with the
$\delta \theta$ so the beam is not always maintained as short as 70 fs but varies from 70 fs to 495 fs. Figure 7 shows the retrieved angular dispersion ADexp. The data were compared with the ![]() $4\times 4$ Kostenbauder matrix model[Reference Kostenbauder20–Reference Chauhan, Cohen and Trebino22], widely used to characterize STCs[Reference Akturk, Gu, Zeek and Trebino2, Reference Akturk, Gu, Gabolde and Trebino23], and showed excellent agreement. The average experimental error for the AD was 0.11 μrad/nm, in agreement with the value estimated by the analysis algorithm.
$4\times 4$ Kostenbauder matrix model[Reference Kostenbauder20–Reference Chauhan, Cohen and Trebino22], widely used to characterize STCs[Reference Akturk, Gu, Zeek and Trebino2, Reference Akturk, Gu, Gabolde and Trebino23], and showed excellent agreement. The average experimental error for the AD was 0.11 μrad/nm, in agreement with the value estimated by the analysis algorithm.
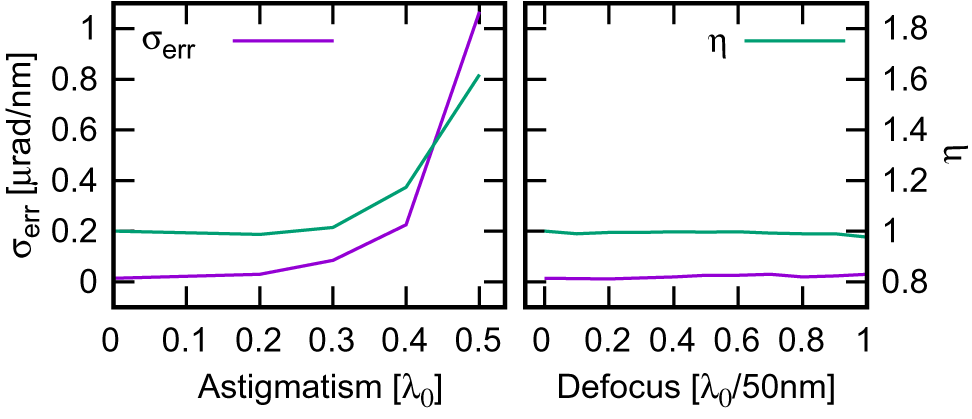
Figure 5 Influence on calibration ![]() $\eta$ and retrieved error
$\eta$ and retrieved error ![]() ${\sigma}_{\rm err}$ of various beam parameters: (left) astigmatism; (right) chromatic defocus.
${\sigma}_{\rm err}$ of various beam parameters: (left) astigmatism; (right) chromatic defocus.

Figure 6 Schematic of the experimental setup implemented in the front end of the FLAME laser system. BS, beam splitter; CCD, charge-coupled device camera; L, achromatic doublet; MK, diffractive mask.
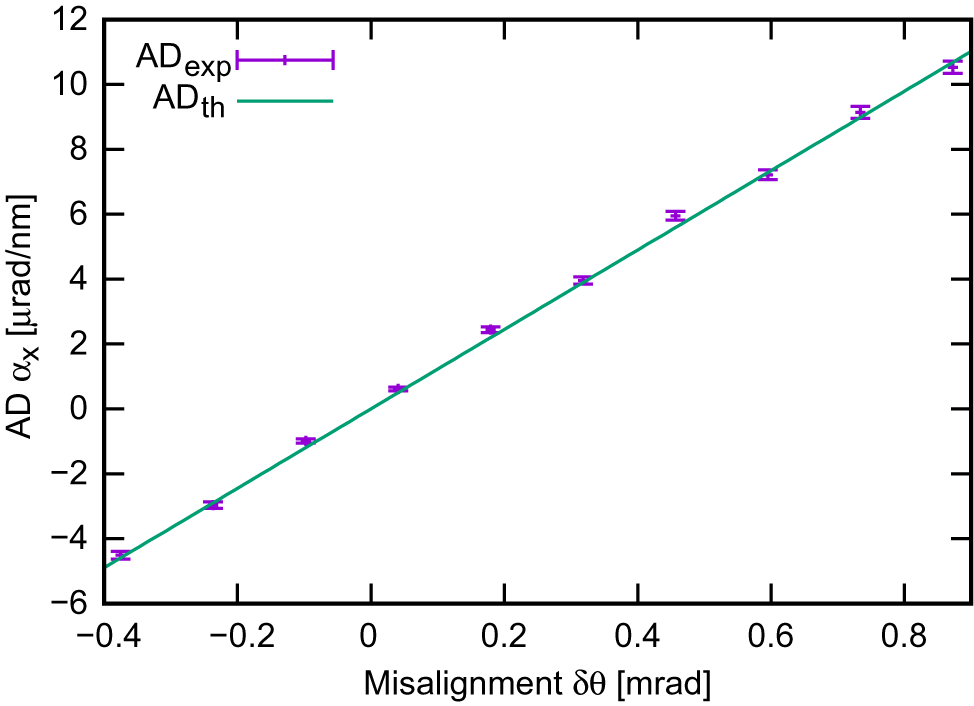
Figure 7 AD as a function of the introduced misalignment ![]() $\delta \theta$. Experimental results (ADexp) compared with the
$\delta \theta$. Experimental results (ADexp) compared with the ![]() $4\times 4$ Kostenbauder matrix formalism simulation (ADth) simulating a misaligned double-pass grating compressor.
$4\times 4$ Kostenbauder matrix formalism simulation (ADth) simulating a misaligned double-pass grating compressor.
In conclusion, AD retrieval is important for determining the performances of ultrashort high-power lasers. The proposed single-shot diagnostic, requiring a minimal number of optics and a compact layout, could be used as a real-time diagnostic, both on a high repetition rate (tens of hertz) laser system and on a low repetition rate, high-power, large laser system. Moreover, the ability to be applied also to stretched pulses will allow monitoring of AD across the entire amplification chain. The performances of the instrument were tested numerically and experimentally, proving to be robust and accurate over a wide range of parameters. Finally, thanks to the retrieval algorithm flexibility, more advanced analysis could be developed and implemented in future to perform real-time measurements of higher-order chromatic aberrations.























