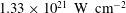With the rapid development of laser technology[Reference Mourou, Tajima and Bulanov1–Reference Yanovsky, Chvykov, Kalinchenko, Rousseau, Planchon, Matsuoka, Maksimchuk, Nees, Cheriaux, Mourou and Krushelnick3], the use of ultra-intense laser irradiation on ultra-thin foils has been studied for various fields ranging from fast ignition for inertial confinement fusion[Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason4, Reference Naumova, Schlegel, Tikhonchuk, Labaune, Sokolov and Mourou5], medical therapy[Reference Bulanov, Esirkepov, Khoroshkov, Kuznetsov and Pegoraro6, Reference Bulanov and Khoroshkov7], and laboratory astrophysics[Reference Remington8], to the generation of high-energy particle sources[Reference Mourou, Tajima and Bulanov1]. However, prepulses or laser pulses with slowly increasing fronts may lead to premature ionization of the target, and significant expansion of the plasma sheet occurs before the amplitude peak of the pulse arrives[Reference Wang, Zhang, Wu, Jiao, Wu, Zhu, Dong, Hong, Gu, Shen, Xu, Leng, Li and Xu9, Reference Wang, Shen, Zhang, Xu, Li, Lu, Wang, Liu, Lu, Shi, Leng, Liang, Li, Wang and Xu10]. These events jeopardize the relativistic interaction of the ultra-thin target. Thus, high-contrast[Reference Wang, Zhang, Wu, Jiao, Wu, Zhu, Dong, Hong, Gu, Shen, Xu, Leng, Li and Xu9–Reference Xu, Wang, Huang, Li, Lu and Leng20] and short-duration laser pulses[Reference Tavella, Nomura, Veisz, Pervak, Marcinkevicius and Krausz21, Reference Ji, Shen, Zhang, Wang, Jin, Xia, Wen, Wang, Xu and Yu22] are needed.
Plasma mirrors may be a feasible method by which to solve these problems. Using a double plasma mirror[Reference Wittmann, Geindre, Audebert, Marjoribanks, Rousseau, Burgy, Douillet, Lefrou, Ta Phuok and Chambaret23], the laser contrast may be improved to
![]() ${\sim }10^{-12}$
at the picosecond time scale[Reference Henig, Kiefer, Markey, Gautier, Flippo, Letzring, Johnson, Shimada, Yin, Albright, Bowers, Fernańdez, Rykovanov, Wu, Zepf, Jung, Liechtenstein, Schreiber, Habs and Hegelich12]. A 30 nm thick carbon foil irradiated by such a high-contrast laser at an intensity of
${\sim }10^{-12}$
at the picosecond time scale[Reference Henig, Kiefer, Markey, Gautier, Flippo, Letzring, Johnson, Shimada, Yin, Albright, Bowers, Fernańdez, Rykovanov, Wu, Zepf, Jung, Liechtenstein, Schreiber, Habs and Hegelich12]. A 30 nm thick carbon foil irradiated by such a high-contrast laser at an intensity of
![]() ${\sim }7 \times 10^{19}\ {\rm W}\ {\rm cm}^{-2}$
can produce a 185 MeV carbon ion beam. A few-cycle laser pulse with an intensity up to
${\sim }7 \times 10^{19}\ {\rm W}\ {\rm cm}^{-2}$
can produce a 185 MeV carbon ion beam. A few-cycle laser pulse with an intensity up to
![]() $3\times 10^{20}\ {\rm W}\ {\rm cm}^{-2}$
may also be generated when a laser irradiates an ultra-thin foil[Reference Ji, Shen, Zhang, Wang, Jin, Xia, Wen, Wang, Xu and Yu22]. In this method, the pulse duration and intensity mainly depend on the laser profile and foil conditions. Generally, the intensity of few-cycle laser pulses is limited in conventional optical methods[Reference Tavella, Nomura, Veisz, Pervak, Marcinkevicius and Krausz21] because of the relatively low damage threshold of the optical components and other problems. However, no laser intensity due to material damage would be limited by this method, because this process only involves laser–plasma interactions, like the plasma grating[Reference Wu, Sheng and Zhang24].
$3\times 10^{20}\ {\rm W}\ {\rm cm}^{-2}$
may also be generated when a laser irradiates an ultra-thin foil[Reference Ji, Shen, Zhang, Wang, Jin, Xia, Wen, Wang, Xu and Yu22]. In this method, the pulse duration and intensity mainly depend on the laser profile and foil conditions. Generally, the intensity of few-cycle laser pulses is limited in conventional optical methods[Reference Tavella, Nomura, Veisz, Pervak, Marcinkevicius and Krausz21] because of the relatively low damage threshold of the optical components and other problems. However, no laser intensity due to material damage would be limited by this method, because this process only involves laser–plasma interactions, like the plasma grating[Reference Wu, Sheng and Zhang24].
Ref. [Reference Ji, Shen, Zhang, Wang, Jin, Xia, Wen, Wang, Xu and Yu22] discusses the generation of a short-cycle laser pulse. It is also necessary to discuss an explicit explanation of the difference and the progress. Ref. [Reference Ji, Shen, Zhang, Wang, Jin, Xia, Wen, Wang, Xu and Yu22] considers in detail the transmission of the incident laser pulse in constant conditions. There the electron layer is assumed to be at rest, and the ion motion effects are not considered. In fact the ion motion can significantly modulate the transmission of the laser. For example, the Doppler effect on the mirror is enhanced because the velocities of the ions initially in the middle of the foil are higher than that of the compressed electron layer (CEL) during the hole-boring stage. The rear part of the incident laser pulse can be reflected in this case.
In this letter, the effects of ion motion on the generation of short-cycle relativistic laser pulses are investigated by analytical modeling and particle-in-cell (PIC) simulations. The generation of a near single-cycle laser pulse has been obtained in the simulations, and the corresponding theoretical analysis has been discussed[Reference Ji, Shen, Zhang, Wang, Jin, Xia, Wen, Wang, Xu and Yu22]. However, all the solutions are based on static conditions, where the motions of the CEL and ions are not included. In fact the ion motion can significantly modulate the transmission of the laser. For example, the Doppler effect on the electron layer mirror is enhanced because the velocities of the ions initially in the middle of the foil are higher than that of the CEL during the hole-boring stage. At the end, the incident laser pulse can be further reflected. One-dimensional (1D) PIC simulations show that the ion motion can further modulate the transmitted short-cycle pulse compared with the case of the electron shutter only. No transmitted pulse is generated when the ions are accelerated together with the CEL at the end of the hole-boring stage. The dynamics of the electrons and ions during laser–plasma interaction are investigated using a simple model. A 3.9 fs laser pulse with an intensity of
![]() $1.33\times 10^{21}\ {\rm W}\ {\rm cm}^{-2}$
is generated by properly controlling the electrons and ions in two-dimensional (2D) PIC simulations. Such a short-cycle high-intensity laser pulse has important applications in single attosecond pulse generation[Reference Brabec and Krausz25] and electron acceleration in a small bubble regime[Reference Pukhov and Meyer-ter-Vehn26, Reference Schmid, Veisz, Tavella, Benavides, Tautz, Herrmann, Buck, Hidding, Marcinkevicius, Schramm, Geissler, Meyer-ter-Vehn, Habs and Krausz27].
$1.33\times 10^{21}\ {\rm W}\ {\rm cm}^{-2}$
is generated by properly controlling the electrons and ions in two-dimensional (2D) PIC simulations. Such a short-cycle high-intensity laser pulse has important applications in single attosecond pulse generation[Reference Brabec and Krausz25] and electron acceleration in a small bubble regime[Reference Pukhov and Meyer-ter-Vehn26, Reference Schmid, Veisz, Tavella, Benavides, Tautz, Herrmann, Buck, Hidding, Marcinkevicius, Schramm, Geissler, Meyer-ter-Vehn, Habs and Krausz27].
Figure 1 shows the interaction model. As an intense circularly polarized (CP) laser pulse irradiates a thin foil, the laser pressure[Reference Shen and Xu28–Reference Yu, Pukhov, Shvets and Chen36] quickly sweeps all electrons forward in a compressed layer. Initially, the protons are left behind because their mass (
![]() $m_{i}=1836m_{e}$
) is much larger than the electron mass
$m_{i}=1836m_{e}$
) is much larger than the electron mass
![]() $m_{e}$
. As the CEL is further pushed forward, the maximum charge separation field at the surface of the compressed layer increases with the depletion distance
$m_{e}$
. As the CEL is further pushed forward, the maximum charge separation field at the surface of the compressed layer increases with the depletion distance
![]() $d$
. When the CEL reaches the back side of the target, as shown in Figure 1, the charge separation field,
$d$
. When the CEL reaches the back side of the target, as shown in Figure 1, the charge separation field,
![]() $E_{0}=4\pi en_{0}d$
, becomes larger. At this stage, the front portion of the pulse with the smaller intensity is reflected by the foil, while the portion with the larger intensity begins to propagate through the foil[Reference Vshivkov, Naumova, Pegoraro and Bulanov37]. As the ions catch up with the electron layer, the transmission is reduced and the rear portion of the pulse is reflected by the foil. Thus, only the part of the laser pulse with the highest intensity is transmitted with a much shorter duration than the incident pulse.
$E_{0}=4\pi en_{0}d$
, becomes larger. At this stage, the front portion of the pulse with the smaller intensity is reflected by the foil, while the portion with the larger intensity begins to propagate through the foil[Reference Vshivkov, Naumova, Pegoraro and Bulanov37]. As the ions catch up with the electron layer, the transmission is reduced and the rear portion of the pulse is reflected by the foil. Thus, only the part of the laser pulse with the highest intensity is transmitted with a much shorter duration than the incident pulse.

Figure 1. Scheme for generating nearly single-cycle laser pulses. The incident pulse irradiates a thin foil, producing an ultra-short transmitted pulse and a reflected pulse. Electrostatic fields
![]() $E_{x1}$
(green dashed line) and
$E_{x1}$
(green dashed line) and
![]() $E_{x2}$
(green dotted line) are produced at both sides of the surface (at
$E_{x2}$
(green dotted line) are produced at both sides of the surface (at
![]() $x=d$
) of the CEL (red solid line) at the initial stage of the interaction. Ions (blue solid line) remain at rest. The distribution of the electrons corresponds to the case where the CEL just reaches the back side of the target. The CEL then oscillates and disperses, as shown in Figures 2c and 2d.
$x=d$
) of the CEL (red solid line) at the initial stage of the interaction. Ions (blue solid line) remain at rest. The distribution of the electrons corresponds to the case where the CEL just reaches the back side of the target. The CEL then oscillates and disperses, as shown in Figures 2c and 2d.

Figure 2. 1D PIC simulation results for
![]() $a_0/t_{{\rm up}}=7.35$
(
$a_0/t_{{\rm up}}=7.35$
(
![]() $a_0=30$
and
$a_0=30$
and
![]() $t_{{\rm up}}=4.08T_0$
),
$t_{{\rm up}}=4.08T_0$
),
![]() $n_0=8n_c$
, and
$n_0=8n_c$
, and
![]() $l_0=1.03\lambda $
. (a) Electron and proton trajectories and their density peaks versus time. (b) Laser profile (blue solid line) and charge density of electrons (black solid line) and ions (red solid line) at
$l_0=1.03\lambda $
. (a) Electron and proton trajectories and their density peaks versus time. (b) Laser profile (blue solid line) and charge density of electrons (black solid line) and ions (red solid line) at
![]() $t=40T_0$
for the case of moving ions. (c) Electron and proton trajectories and (d) laser profile (blue solid line) and charge density of electrons (black solid line) and ions (red solid line) at
$t=40T_0$
for the case of moving ions. (c) Electron and proton trajectories and (d) laser profile (blue solid line) and charge density of electrons (black solid line) and ions (red solid line) at
![]() $t=40T_0$
for the case of ions at rest.
$t=40T_0$
for the case of ions at rest.
1D PIC simulations are used to study the effects of ion motion on the generation of a short-cycle relativistic laser pulse. A CP laser pulse with wavelength
![]() $\lambda =1\ \mu {\rm m}$
is incident on the target from the left boundary. The laser front arrives at the front surface of the target at
$\lambda =1\ \mu {\rm m}$
is incident on the target from the left boundary. The laser front arrives at the front surface of the target at
![]() $t=20T_0$
, where
$t=20T_0$
, where
![]() $T_0=\lambda /c$
is the laser cycle and
$T_0=\lambda /c$
is the laser cycle and
![]() $c$
is the speed of light. The laser pulse has a trapezoidal shape profile (linear growth–plateau–linear decrease) with a duration of
$c$
is the speed of light. The laser pulse has a trapezoidal shape profile (linear growth–plateau–linear decrease) with a duration of
![]() $9.66T_0$
(
$9.66T_0$
(
![]() $4.08T_0-1.5T_0-4.08T_0$
). Here, the short width of the flat top (
$4.08T_0-1.5T_0-4.08T_0$
). Here, the short width of the flat top (
![]() $1.5T_0$
) is used to reduce the content of high frequencies. The frequency of the trapezoidal laser pulse used in this case is mainly at the base frequency
$1.5T_0$
) is used to reduce the content of high frequencies. The frequency of the trapezoidal laser pulse used in this case is mainly at the base frequency
![]() $c/\lambda $
. The laser amplitude gradient is
$c/\lambda $
. The laser amplitude gradient is
![]() $a_{0}/t_{\mathrm{up}}=7.35$
(
$a_{0}/t_{\mathrm{up}}=7.35$
(
![]() $a_{0}=30$
and
$a_{0}=30$
and
![]() $t_{\mathrm{up}}=4.08T_0$
). Here,
$t_{\mathrm{up}}=4.08T_0$
). Here,
![]() $a_{0}=eE_{L}/m_{e}\omega _{L}c$
is the normalized amplitude, where
$a_{0}=eE_{L}/m_{e}\omega _{L}c$
is the normalized amplitude, where
![]() $m_{e}$
and
$m_{e}$
and
![]() $e$
are the electron mass and charge, respectively,
$e$
are the electron mass and charge, respectively,
![]() $E_{L}$
is the laser electric field,
$E_{L}$
is the laser electric field,
![]() $\omega _{L}$
is the laser frequency, and
$\omega _{L}$
is the laser frequency, and
![]() $t_{\mathrm{up}}$
is the rising time of the laser pulse. The front surface of the target is located at
$t_{\mathrm{up}}$
is the rising time of the laser pulse. The front surface of the target is located at
![]() $x=20\lambda $
. The foil density is
$x=20\lambda $
. The foil density is
![]() $n_{0}=8n_{c}$
and the foil thickness is
$n_{0}=8n_{c}$
and the foil thickness is
![]() $l_{0}=1.03\lambda $
. Here,
$l_{0}=1.03\lambda $
. Here,
![]() $n_{c}=\omega _{L}^{2}m_{e}/4\pi e^{2}$
is the critical density. Low-density plasma with a step density profile is used to simplify the model and reduce the simulation time. The longitudinal length of the 1D simulation box is
$n_{c}=\omega _{L}^{2}m_{e}/4\pi e^{2}$
is the critical density. Low-density plasma with a step density profile is used to simplify the model and reduce the simulation time. The longitudinal length of the 1D simulation box is
![]() $x=60\lambda $
. The mesh size is
$x=60\lambda $
. The mesh size is
![]() $\lambda /200$
. Each cell contains 100 numerical macro particles in the plasma region.
$\lambda /200$
. Each cell contains 100 numerical macro particles in the plasma region.
Figure 2a shows the evolution of electrons and ions. The laser front arrives at the front surface of the foil at
![]() $t=20T_0$
, and the electrons are pushed forward in a thin compressed layer. The peak density of the layer increases with time. Both the CEL and the amplitude peak of the incident laser pulse arrive at the back side of the foil (
$t=20T_0$
, and the electrons are pushed forward in a thin compressed layer. The peak density of the layer increases with time. Both the CEL and the amplitude peak of the incident laser pulse arrive at the back side of the foil (
![]() $x=21.03\lambda $
) at
$x=21.03\lambda $
) at
![]() $t\sim 25.3T_0$
. The peak density of the CEL is
$t\sim 25.3T_0$
. The peak density of the CEL is
![]() $n=192.5n_{c}$
at this time. Then, the electron layer begins to disperse in the vacuum, and the density decreases sharply to
$n=192.5n_{c}$
at this time. Then, the electron layer begins to disperse in the vacuum, and the density decreases sharply to
![]() $n=143.9n_{c}$
[Figure 2a]. The incident pulse begins to transmit. However, the electron density increases again up to
$n=143.9n_{c}$
[Figure 2a]. The incident pulse begins to transmit. However, the electron density increases again up to
![]() $n=406\cdot 4n_{c}$
at
$n=406\cdot 4n_{c}$
at
![]() $t\sim 26T_0$
. The ions catch up with the CEL, forming a double layer with the electrons. The remainder part of the incident pulse is then reflected and the transmitted field drops sharply from its peak value. Figure 2b shows that a short-cycle transmitted laser pulse with a duration of
$t\sim 26T_0$
. The ions catch up with the CEL, forming a double layer with the electrons. The remainder part of the incident pulse is then reflected and the transmitted field drops sharply from its peak value. Figure 2b shows that a short-cycle transmitted laser pulse with a duration of
![]() ${\sim }0.9T_0$
and amplitude peak
${\sim }0.9T_0$
and amplitude peak
![]() $a_{t}=16$
is produced. Here, we consider the cases that the shortening of the incident laser pulse does not seriously depend on the harmonic generation. The central frequency is barely changed, meaning that there is almost no frequency shift compared with the incident laser pulse. The number of lightwave cycles is indeed reduced by the pulse shortening in our case. The frequency broadening should be taken into account when the duration of the transmitted pulse is much shorter than the laser period, which is not considered in this paper. Figures 2c and 2d show the case of ions at rest. The duration of the transmitted laser pulse increases to
$a_{t}=16$
is produced. Here, we consider the cases that the shortening of the incident laser pulse does not seriously depend on the harmonic generation. The central frequency is barely changed, meaning that there is almost no frequency shift compared with the incident laser pulse. The number of lightwave cycles is indeed reduced by the pulse shortening in our case. The frequency broadening should be taken into account when the duration of the transmitted pulse is much shorter than the laser period, which is not considered in this paper. Figures 2c and 2d show the case of ions at rest. The duration of the transmitted laser pulse increases to
![]() $2.8T_0$
at this point [Figure 2d]. Compared with Figures 2b and 2d, the ion motion has an important role in modulating the rear part of the incident laser pulse.
$2.8T_0$
at this point [Figure 2d]. Compared with Figures 2b and 2d, the ion motion has an important role in modulating the rear part of the incident laser pulse.
The simulations above show that the ion motion is important for the generation of short-cycle laser pulses. The main reason is that the re-entering of the ions into the CEL at the back side of the foil can further reflect the rear part of the laser pulse. In the case of Figure 2a, the laser pulse begins to transmit the foil as the CEL slightly disperses at the back side of the foil. Then the ions re-enter into the CEL, and a double-layer reflecting mirror is produced. In this stage, the Doppler effect on the mirror is enhanced because the velocities of the ions initially in the middle of the foil are higher than that of the CEL during the hole-boring stage. At the end, the rear part of the incident laser pulse is reflected.
The dynamics of the electrons and ions are investigated to obtain insights into the generation of short-cycle lasers. The action of the electric field in the CEL
![]() $E_{x2}$
(Figure 1) is initially neglected for ion acceleration because the velocity of the CEL is large[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu35]. Moreover, the ions do not catch the CEL when this layer arrives at the back side of the target[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu35]. Here, the unrelativistic interaction of the laser pulse with the linearly increasing front in the hole-boring stage is considered to simplify our study. A time-dependent theory model can be used to deal with the relativistic interaction of the laser with any pulse profile in Ref. [Reference Wang, Shen, Zhang, Ji, Yu, Yi, Wang and Xu38].
$E_{x2}$
(Figure 1) is initially neglected for ion acceleration because the velocity of the CEL is large[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu35]. Moreover, the ions do not catch the CEL when this layer arrives at the back side of the target[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu35]. Here, the unrelativistic interaction of the laser pulse with the linearly increasing front in the hole-boring stage is considered to simplify our study. A time-dependent theory model can be used to deal with the relativistic interaction of the laser with any pulse profile in Ref. [Reference Wang, Shen, Zhang, Ji, Yu, Yi, Wang and Xu38].
For electrons, a uniform velocity of the CEL can be obtained for a laser with a linearly increasing front in simulations[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu35]. The electrons are first accelerated by the ponderomotive force of the CP laser pulse within a very short time, and then a balance between the laser pressure and the electrostatic forces appears. Then the swept electrons pile up to form a dense skin-depth layer by the laser pressure and electrostatic forces. We define this skin-depth layer as the CEL. The equation of motion of a perfectly reflecting mirror,
![]() ${\rm d}p/{\rm d}t=P{\rm d}\sigma $
, can be used to describe the motion of the CEL, where
${\rm d}p/{\rm d}t=P{\rm d}\sigma $
, can be used to describe the motion of the CEL, where
![]() $p$
is the momentum of the mirror element,
$p$
is the momentum of the mirror element,
![]() ${\rm d}\sigma $
is the element of area of the mirror and normal to the mirror surface, and
${\rm d}\sigma $
is the element of area of the mirror and normal to the mirror surface, and
![]() $P$
is the radiation pressure[Reference Pegoraro and Bulanov39]. In this paper, we focus on the case that the ions move after the electrons during the hole-boring stage because the laser-pulse front is very sharp. The laser energy is largely contained in the charge separation field during this stage. The velocities of the electron layer and ions are not relativistic. Simulations have shown that the surface of the CEL moves roughly at a constant velocity; if the laser-pulse front is linearly increasing and short enough, there must be a balance between the electrostatic force and the laser pressure force[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu35],
$P$
is the radiation pressure[Reference Pegoraro and Bulanov39]. In this paper, we focus on the case that the ions move after the electrons during the hole-boring stage because the laser-pulse front is very sharp. The laser energy is largely contained in the charge separation field during this stage. The velocities of the electron layer and ions are not relativistic. Simulations have shown that the surface of the CEL moves roughly at a constant velocity; if the laser-pulse front is linearly increasing and short enough, there must be a balance between the electrostatic force and the laser pressure force[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu35],
where the normalized amplitude of the laser on the moving CEL surface
![]() $a=(a_{0}/t_{\mathrm{up}})(t-v_{{\rm CEL}}t)$
, and
$a=(a_{0}/t_{\mathrm{up}})(t-v_{{\rm CEL}}t)$
, and
![]() $l = v_{{\rm CEL}}t$
. Here,
$l = v_{{\rm CEL}}t$
. Here,
![]() $v_{\mathrm{CEL}}$
,
$v_{\mathrm{CEL}}$
,
![]() $t_{\mathrm{up}}$
, and
$t_{\mathrm{up}}$
, and
![]() $n_{0}$
are normalized by
$n_{0}$
are normalized by
![]() $c$
,
$c$
,
![]() $\lambda /c$
, and
$\lambda /c$
, and
![]() $n_{c} =\omega _{L}^{2} m_{e}/ 4\pi e^{2}$
, respectively. Although the linear amplitude increases, a part of the electrons is moving while another part is stationary; most electrons move around a averaged velocity during the hole-boring stage. Such averaged velocity of the skin-depth reflecting mirror has been verified in the simulations[Reference Wang, Shen, Zhang, Ji, Yu, Yi, Wang and Xu38]. Equation (1) describes the velocity of the CEL for the case that the laser is totally reflected by the plasma. The transmission of the laser pulse is not considered during the hole-boring stage in our case. Based on Equation (1), a uniform velocity of the CEL (
$n_{c} =\omega _{L}^{2} m_{e}/ 4\pi e^{2}$
, respectively. Although the linear amplitude increases, a part of the electrons is moving while another part is stationary; most electrons move around a averaged velocity during the hole-boring stage. Such averaged velocity of the skin-depth reflecting mirror has been verified in the simulations[Reference Wang, Shen, Zhang, Ji, Yu, Yi, Wang and Xu38]. Equation (1) describes the velocity of the CEL for the case that the laser is totally reflected by the plasma. The transmission of the laser pulse is not considered during the hole-boring stage in our case. Based on Equation (1), a uniform velocity of the CEL (
![]() $v_{{\rm CEL}}\approx 0.194c$
) is obtained for
$v_{{\rm CEL}}\approx 0.194c$
) is obtained for
![]() $a_{0}=30$
,
$a_{0}=30$
,
![]() $t_{\mathrm{up}}=4.08T$
,
$t_{\mathrm{up}}=4.08T$
,
![]() $n_{0}=8n_{c}$
, and
$n_{0}=8n_{c}$
, and
![]() $l_{0}=1.03\lambda $
, which is consistent with the simulation result in Figure 2a.
$l_{0}=1.03\lambda $
, which is consistent with the simulation result in Figure 2a.
For ions, the velocity for the ion initially at rest at
![]() $x_{10}$
(
$x_{10}$
(
![]() $0<x_{10}<d$
) can be approximated by[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu35]
$0<x_{10}<d$
) can be approximated by[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu35]
where
![]() $x_{10}$
,
$x_{10}$
,
![]() $x_{i1}$
, and
$x_{i1}$
, and
![]() $d$
are normalized by
$d$
are normalized by
![]() $\lambda $
, and the ion mass
$\lambda $
, and the ion mass
![]() $m_{i}$
and charge
$m_{i}$
and charge
![]() $q_{i}$
are normalized by
$q_{i}$
are normalized by
![]() $m_{e}$
and
$m_{e}$
and
![]() $e$
, respectively. In addition, the action time
$e$
, respectively. In addition, the action time
![]() $t_{1}$
is normalized by
$t_{1}$
is normalized by
![]() $\lambda /c$
.
$\lambda /c$
.
![]() $E_{0}=2\pi n_{0}d$
is the maximum electrostatic field of charge depletion, which is normalized by
$E_{0}=2\pi n_{0}d$
is the maximum electrostatic field of charge depletion, which is normalized by
![]() $e/m_{e}\omega _{L}c$
.
$e/m_{e}\omega _{L}c$
.
![]() $E_{0}=2\pi n_{0}l_{0}$
is obtained when the CEL is assumed to be superthin (
$E_{0}=2\pi n_{0}l_{0}$
is obtained when the CEL is assumed to be superthin (
![]() $d\approx l_{0}$
)[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu35]. For the case shown in Figure 2a,
$d\approx l_{0}$
)[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu35]. For the case shown in Figure 2a,
![]() $E_{0}\approx 52$
for
$E_{0}\approx 52$
for
![]() $n_{0}=8n_{c}$
, and
$n_{0}=8n_{c}$
, and
![]() $l_{0}=1.03\lambda $
.
$l_{0}=1.03\lambda $
.
The velocity of the ions initially at rest in the middle of the foil (
![]() $x_{10}=d/2$
)
$x_{10}=d/2$
)
![]() $v_{i1}\sim 0.24c$
is obtained using Equation (2). Here,
$v_{i1}\sim 0.24c$
is obtained using Equation (2). Here,
![]() $t_{1}\sim 0.5d/v_{\mathrm{CEL}}$
is used. Ions initially resting in the middle of the foil run fast during the sharp-front laser interaction at the end of the hole-boring stage[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu35]. The CEL quickly catches up to these ions after the hole-boring stage because the electron mass is much smaller than the ion mass. Therefore, we can assume that
$t_{1}\sim 0.5d/v_{\mathrm{CEL}}$
is used. Ions initially resting in the middle of the foil run fast during the sharp-front laser interaction at the end of the hole-boring stage[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu35]. The CEL quickly catches up to these ions after the hole-boring stage because the electron mass is much smaller than the ion mass. Therefore, we can assume that
![]() $v_{\mathrm{CEL}}\sim 0.24c$
at this point, which is larger than the velocity of the CEL (
$v_{\mathrm{CEL}}\sim 0.24c$
at this point, which is larger than the velocity of the CEL (
![]() ${\sim }0.194c$
) during the hole-boring stage. The Doppler effect parameter
${\sim }0.194c$
) during the hole-boring stage. The Doppler effect parameter
![]() $(c-v_{\mathrm{CEL}})/(c+v_{\mathrm{CEL}})$
is thus reduced by the ion motion. Moreover, the reflection of the laser pulse is enhanced. The rear part of the transmitted pulse can be further modulated by the ion motion compared with the case of the electron shutter only, which is verified by the simulations in Figures 2a–2d.
$(c-v_{\mathrm{CEL}})/(c+v_{\mathrm{CEL}})$
is thus reduced by the ion motion. Moreover, the reflection of the laser pulse is enhanced. The rear part of the transmitted pulse can be further modulated by the ion motion compared with the case of the electron shutter only, which is verified by the simulations in Figures 2a–2d.
From the discussion above, two conditions are required for the generation of an intense short-cycle transmitted pulse. First, the peak of the incident pulse must arrive at the back surface when the CEL disperses, thereby generating a short-duration transmitted pulse with higher amplitude. This condition is simply an approximation because the exact amplitude of the transmitted pulse is not considered. Second, the ions must not catch up to the CEL during the hole-boring stage. Otherwise all of the laser pulses may be reflected.
For the first condition, the laser and foil parameters are as follows:
where
![]() $a_{\mathrm{open}}$
is the peak amplitude of the incident laser pulse that may open the electron shutter. For a certain laser amplitude
$a_{\mathrm{open}}$
is the peak amplitude of the incident laser pulse that may open the electron shutter. For a certain laser amplitude
![]() $a_{\mathrm{open}}=a_{0}$
and gradient
$a_{\mathrm{open}}=a_{0}$
and gradient
![]() $a_{0}/t_{\mathrm{up}}$
, the incident laser can transmit if
$a_{0}/t_{\mathrm{up}}$
, the incident laser can transmit if
![]() $l_{0}<t_{\mathrm{up}}\cdot v_{\mathrm{CEL}}/(1- v_{\mathrm{CEL}})$
according to Equation (3). Here,
$l_{0}<t_{\mathrm{up}}\cdot v_{\mathrm{CEL}}/(1- v_{\mathrm{CEL}})$
according to Equation (3). Here,
![]() $v_{\mathrm{CEL}}$
is calculated using Equation (1). The laser peak cannot reach the back side of the target when
$v_{\mathrm{CEL}}$
is calculated using Equation (1). The laser peak cannot reach the back side of the target when
![]() $l_{0}\gg t_{\mathrm{up}}\cdot v_{\mathrm{CEL}}/ (1-v_{\mathrm{CEL}})$
. In this case, the incident laser is completely reflected, and no transmitted laser pulse can be generated. For the case shown in Figure 2,
$l_{0}\gg t_{\mathrm{up}}\cdot v_{\mathrm{CEL}}/ (1-v_{\mathrm{CEL}})$
. In this case, the incident laser is completely reflected, and no transmitted laser pulse can be generated. For the case shown in Figure 2,
![]() $l_{0}<0.98\lambda $
is obtained for
$l_{0}<0.98\lambda $
is obtained for
![]() $a_{0}/t_{\mathrm{up}}=7.35$
(
$a_{0}/t_{\mathrm{up}}=7.35$
(
![]() $a_{0}=30$
and
$a_{0}=30$
and
![]() $t_{\mathrm{up}}=4.08T_0$
), and
$t_{\mathrm{up}}=4.08T_0$
), and
![]() $n_{0}=8n_{c}$
, which is consistent with the simulation results (Figure 3). Figure 3 shows that the transmitted laser pulse with
$n_{0}=8n_{c}$
, which is consistent with the simulation results (Figure 3). Figure 3 shows that the transmitted laser pulse with
![]() $a_{0}>30$
is generated for
$a_{0}>30$
is generated for
![]() $l_{0}<0.98\lambda $
. A nearly single-cycle laser pulse is generated for
$l_{0}<0.98\lambda $
. A nearly single-cycle laser pulse is generated for
![]() $l_{0}=1.03\lambda $
, as shown in Figure 3.
$l_{0}=1.03\lambda $
, as shown in Figure 3.

Figure 3. (a) Amplitude peak
![]() $a_t$
(black square) and duration (blue triangle) of transmitted pulses versus foil thickness
$a_t$
(black square) and duration (blue triangle) of transmitted pulses versus foil thickness
![]() $l_0$
. For the incident laser,
$l_0$
. For the incident laser,
![]() $a_0/t_{{\rm up}}=7.35$
(
$a_0/t_{{\rm up}}=7.35$
(
![]() $a_0=30$
and
$a_0=30$
and
![]() $t_{{\rm up}}=4.08T_0$
). The foil density is
$t_{{\rm up}}=4.08T_0$
). The foil density is
![]() $n_0=8n_c$
. Laser profile (blue solid line) and charge density of electrons (black solid line) and ions (red solid line) for
$n_0=8n_c$
. Laser profile (blue solid line) and charge density of electrons (black solid line) and ions (red solid line) for
![]() $a_0/t_{{\rm up}}=7.35$
(
$a_0/t_{{\rm up}}=7.35$
(
![]() $a_0=40.4$
and
$a_0=40.4$
and
![]() $t_{{\rm up}}=5.5T_0$
) and (b)
$t_{{\rm up}}=5.5T_0$
) and (b)
![]() $l_0=1.32\lambda $
, (c)
$l_0=1.32\lambda $
, (c)
![]() $1.2\lambda $
.
$1.2\lambda $
.
For the second condition, the laser and foil parameters are[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu35]
where
![]() $l_{0} =\sqrt{2m_{i}/q_{i} n_{0}} v_{{\rm CEL}}/\pi $
corresponds to the case where ions are initially in the middle of the foil and the CEL reaches the back surface of the foil at the same time. The incident laser is completely reflected if
$l_{0} =\sqrt{2m_{i}/q_{i} n_{0}} v_{{\rm CEL}}/\pi $
corresponds to the case where ions are initially in the middle of the foil and the CEL reaches the back surface of the foil at the same time. The incident laser is completely reflected if
![]() $l_{0}\ge \sqrt{2m_{i}/q_{i} n_{0}} v_{{\rm CEL}}/\pi $
[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu35], which is verified by the simulation results in Figure 3.
$l_{0}\ge \sqrt{2m_{i}/q_{i} n_{0}} v_{{\rm CEL}}/\pi $
[Reference Wang, Shen, Zhang, Ji, Wen, Xu, Yu, Li and Xu35], which is verified by the simulation results in Figure 3.
![]() $l_{0}\ge 1.32\lambda $
is obtained for
$l_{0}\ge 1.32\lambda $
is obtained for
![]() $a_{0}/t_{\mathrm{up}}=7.35$
(
$a_{0}/t_{\mathrm{up}}=7.35$
(
![]() $a_{0}=40.4$
and
$a_{0}=40.4$
and
![]() $t_{\mathrm{up}}=5.5T_0$
), and
$t_{\mathrm{up}}=5.5T_0$
), and
![]() $n_{0}=8n_{c}$
. Figure 3b shows that no transmitted laser pulse is generated for
$n_{0}=8n_{c}$
. Figure 3b shows that no transmitted laser pulse is generated for
![]() $l_{0}=1.32\lambda $
. A thinner foil (
$l_{0}=1.32\lambda $
. A thinner foil (
![]() $l_{0}=1.2\lambda $
) is simulated for the same laser and foil parameters to verify the condition of Equation (4). Figure 3c shows that a quasi-single-cycle transmitted pulse is generated, where the ions does not catch up the CEL as the CEL leaves the back surface of the foil. This indicates that ion motion indeed affects the transmitting of the laser pulse. Here, a higher density (
$l_{0}=1.2\lambda $
) is simulated for the same laser and foil parameters to verify the condition of Equation (4). Figure 3c shows that a quasi-single-cycle transmitted pulse is generated, where the ions does not catch up the CEL as the CEL leaves the back surface of the foil. This indicates that ion motion indeed affects the transmitting of the laser pulse. Here, a higher density (
![]() $n_{0}=200n_{c}$
) of the foil is also theoretically estimated. The velocity of the CEL
$n_{0}=200n_{c}$
) of the foil is also theoretically estimated. The velocity of the CEL
![]() $v_{\mathrm{CEL}}\sim 0.07c$
is obtained for an ultra-intense laser pulse (
$v_{\mathrm{CEL}}\sim 0.07c$
is obtained for an ultra-intense laser pulse (
![]() $a_{0}/t_{\mathrm{up}}\sim 54$
) based on Equation (1). Then
$a_{0}/t_{\mathrm{up}}\sim 54$
) based on Equation (1). Then
![]() $l_{0}<0.1\lambda $
can be obtained according to Equation (4). And
$l_{0}<0.1\lambda $
can be obtained according to Equation (4). And
![]() $a_{\mathrm{open}}>57.4$
is obtained for
$a_{\mathrm{open}}>57.4$
is obtained for
![]() $l_{0}=0.08\lambda $
according to Equation (3). In Figure 3c, the duration of the transmitted pulse is much shorter than the laser period when the foil thickness further increases (
$l_{0}=0.08\lambda $
according to Equation (3). In Figure 3c, the duration of the transmitted pulse is much shorter than the laser period when the foil thickness further increases (
![]() $l_{0}>1\lambda $
). The frequency broadening should be taken into account when the duration of the transmitted pulse is much shorter than the laser period, which is not considered in this paper.
$l_{0}>1\lambda $
). The frequency broadening should be taken into account when the duration of the transmitted pulse is much shorter than the laser period, which is not considered in this paper.
Different simulations of carbon ions are also performed to verify the theory. The velocity of the CEL
![]() $v_{\mathrm{CEL}}\sim 0.2c$
is obtained for
$v_{\mathrm{CEL}}\sim 0.2c$
is obtained for
![]() $a_{0}/t_{\mathrm{up}}\sim 15$
and
$a_{0}/t_{\mathrm{up}}\sim 15$
and
![]() $n_{0}=15n_{c}$
according to Equation (1).
$n_{0}=15n_{c}$
according to Equation (1).
![]() $l_{0}<1.4\lambda $
is calculated based on Equation (4) for
$l_{0}<1.4\lambda $
is calculated based on Equation (4) for
![]() ${\rm C}^{6+}$
ions, where
${\rm C}^{6+}$
ions, where
![]() $m_{i}=12$
and
$m_{i}=12$
and
![]() $q_{i}=6$
. Here, the foil thickness
$q_{i}=6$
. Here, the foil thickness
![]() $l_{0}\sim 1.25\lambda $
is used in the simulation. And
$l_{0}\sim 1.25\lambda $
is used in the simulation. And
![]() $a_{0}=80$
is chosen to satisfy the condition
$a_{0}=80$
is chosen to satisfy the condition
![]() $a_{\mathrm{open}}>75$
according to Equation (3). Figure 4 shows that a near single-cycle laser pulse is generated, indicating that the conditions [Equations (3) and (4)] can be used to deal with different ion masses. However, a smaller value of
$a_{\mathrm{open}}>75$
according to Equation (3). Figure 4 shows that a near single-cycle laser pulse is generated, indicating that the conditions [Equations (3) and (4)] can be used to deal with different ion masses. However, a smaller value of
![]() $m_{i}/q_{i}$
is suggested for the generation of a short-cycle transmitted laser pulse. The main reason is that a thinner foil is obtained according to Equation (4), and some multidimensional effects and instabilities can be reduced to a certain extent for a thinner foil.
$m_{i}/q_{i}$
is suggested for the generation of a short-cycle transmitted laser pulse. The main reason is that a thinner foil is obtained according to Equation (4), and some multidimensional effects and instabilities can be reduced to a certain extent for a thinner foil.

Figure 4. Laser profile
![]() $E_y$
(blue solid line) and charge density of electrons (black solid line) and
$E_y$
(blue solid line) and charge density of electrons (black solid line) and
![]() ${\rm C}^{6+}$
ions (red solid line) for
${\rm C}^{6+}$
ions (red solid line) for
![]() $a_0/t_{{\rm up}}=15$
(
$a_0/t_{{\rm up}}=15$
(
![]() $a_0=80$
and
$a_0=80$
and
![]() $t_{{\rm up}}=6T_0$
). The foil density is
$t_{{\rm up}}=6T_0$
). The foil density is
![]() $n_0=15n_c$
, and the foil thickness is
$n_0=15n_c$
, and the foil thickness is
![]() $l_0=1.25\lambda $
.
$l_0=1.25\lambda $
.
A clean laser pulse is used to simplify the model in this work. In fact, the effect of a laser prepulse is always critical for a thin foil and it may alter the conditions [see Equations (3) and (4)]. A density gradient at the front or back side of the foil produced by the prepulse must be considered if the laser contrast is not ultra-high[Reference Wang, Zhang, Wu, Jiao, Wu, Zhu, Dong, Hong, Gu, Shen, Xu, Leng, Li and Xu9, Reference Wang, Shen, Zhang, Xu, Li, Lu, Wang, Liu, Lu, Shi, Leng, Liang, Li, Wang and Xu10]; such a condition is not considered in this work.
To verify our theoretical model, we also carried out 2D PIC simulations. The same parameters as in the 1D PIC simulations [see Figures 2a and 2b], which include
![]() $a_{0}=30$
,
$a_{0}=30$
,
![]() $t_{\mathrm{up}}=4.08T_0$
,
$t_{\mathrm{up}}=4.08T_0$
,
![]() $n_{0}=8n_{c}$
, and
$n_{0}=8n_{c}$
, and
![]() $l_{0}=1.03\lambda $
, are used in the 2D case. The laser pulse has a trapezoidal shape profile
$l_{0}=1.03\lambda $
, are used in the 2D case. The laser pulse has a trapezoidal shape profile
![]() $(4.08T_0-1.5T_0-4.08T_0)$
in time and is a transverse four-order super Gaussian,
$(4.08T_0-1.5T_0-4.08T_0)$
in time and is a transverse four-order super Gaussian,
![]() $I\sim \exp [-(r/r_{0})^{4}]$
, where
$I\sim \exp [-(r/r_{0})^{4}]$
, where
![]() $r_{0}=10\lambda $
. The simulation region is a
$r_{0}=10\lambda $
. The simulation region is a
![]() $50\lambda \times 50\lambda $
box (3000 cells along the laser axis
$50\lambda \times 50\lambda $
box (3000 cells along the laser axis
![]() $x$
, and 3000 cells transversely along axis
$x$
, and 3000 cells transversely along axis
![]() $y$
). The plasma foil occupies the region from
$y$
). The plasma foil occupies the region from
![]() $x=20\lambda $
to
$x=20\lambda $
to
![]() $21.03\lambda $
and from
$21.03\lambda $
and from
![]() $x=-22.5\lambda $
to
$x=-22.5\lambda $
to
![]() $22.5\lambda $
. Ten macroparticles are available in each cell. Absorbing boundaries are used for both electromagnetic waves and macroparticles.
$22.5\lambda $
. Ten macroparticles are available in each cell. Absorbing boundaries are used for both electromagnetic waves and macroparticles.
Figure 5 shows the electron and ion distributions and the laser profile in the (
![]() $x$
,
$x$
,
![]() $y$
) plane at
$y$
) plane at
![]() $t=40T_{0}$
. From the laser axial profiles at
$t=40T_{0}$
. From the laser axial profiles at
![]() $y=0\lambda $
, a nearly single-cycle transmitted pulse is produced. The laser duration is about 3.9 fs (FWHM), and the amplitude peak is
$y=0\lambda $
, a nearly single-cycle transmitted pulse is produced. The laser duration is about 3.9 fs (FWHM), and the amplitude peak is
![]() $a_{t}\sim 22$
(
$a_{t}\sim 22$
(
![]() $I_{0} =2a_{t}^{2}\times 1.37\times 10^{18}\ {\rm W}\ {\rm cm}^{-2}=1.33\times 10^{21}\ {\rm W}\ {\rm cm}^{-2}$
). Compared with the results from 1D simulations in Figure 2b, the duration and amplitude peak are larger in the 2D case, which is mainly attributed to foil deformation and self-focusing of the laser in the ‘hole-boring’ stage. Figure 5 shows that the transmitted laser amplitude decreases sharply from its peak because ions catch the slightly dispersed electron layer at the end of the hole-boring stage. Here, the ion motion further modulates the rear part of the incident laser pulse. In addition, the transverse width is also reduced when the laser mainly passes through the foil. Figure 4 further shows that the transverse width is reduced from
$I_{0} =2a_{t}^{2}\times 1.37\times 10^{18}\ {\rm W}\ {\rm cm}^{-2}=1.33\times 10^{21}\ {\rm W}\ {\rm cm}^{-2}$
). Compared with the results from 1D simulations in Figure 2b, the duration and amplitude peak are larger in the 2D case, which is mainly attributed to foil deformation and self-focusing of the laser in the ‘hole-boring’ stage. Figure 5 shows that the transmitted laser amplitude decreases sharply from its peak because ions catch the slightly dispersed electron layer at the end of the hole-boring stage. Here, the ion motion further modulates the rear part of the incident laser pulse. In addition, the transverse width is also reduced when the laser mainly passes through the foil. Figure 4 further shows that the transverse width is reduced from
![]() $10\lambda $
(FWHM) to about
$10\lambda $
(FWHM) to about
![]() $6\lambda $
(FWHM). The front and back portions of the pulse are reflected after laser–foil interaction. About 92% of the energy of the incident laser pulse is reflected, as shown in Figure 5.
$6\lambda $
(FWHM). The front and back portions of the pulse are reflected after laser–foil interaction. About 92% of the energy of the incident laser pulse is reflected, as shown in Figure 5.

Figure 5. Electron (red circle) and ion (blue circle) distribution and the laser profiles in the (
![]() $x$
,
$x$
,
![]() $y$
) plane for foils with
$y$
) plane for foils with
![]() $n_0=8n_c$
and
$n_0=8n_c$
and
![]() $l_0=1.03$
irradiated by CP laser pulses with
$l_0=1.03$
irradiated by CP laser pulses with
![]() $a_0/t_{{\rm up}}=7.35$
(
$a_0/t_{{\rm up}}=7.35$
(
![]() $a_0=30$
and
$a_0=30$
and
![]() $t_{{\rm up}}=4.08T_0$
) at
$t_{{\rm up}}=4.08T_0$
) at
![]() $t=40T_0$
. The axial laser profiles at
$t=40T_0$
. The axial laser profiles at
![]() $y=0$
are denoted by the black solid lines.
$y=0$
are denoted by the black solid lines.
In conclusion, the effects of ion motion on the generation of a short-cycle relativistic laser pulse are investigated by analytical modeling and PIC simulations. 1D PIC simulations show that the ion shutter can further modulate the transmitted short-cycle pulse compared with the case of the electron shutter only. Two conditions are theoretically proposed to generate short-cycle transmitted laser pulses, which are proven by the simulations. A near single-cycle (3.9 fs) laser pulse with an intensity of
![]() $1.33\times 10^{21}\ {\rm W}\ {\rm cm}^{-2}$
is generated by properly controlling the electron and ion shutters in 2D PIC simulations.
$1.33\times 10^{21}\ {\rm W}\ {\rm cm}^{-2}$
is generated by properly controlling the electron and ion shutters in 2D PIC simulations.
Acknowledgements
This work was supported by the 973 Program (No. 2011CB808104), the National Natural Science Foundation of China (Nos. 11335013, 10834008, 11125526, 60921004, and 11305236), the International S&T Cooperation Program of China (No. 2011DFA11300), and Shanghai Natural Science Foundation (No. 13ZR1463300).