Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T02:02:46.200Z Has data issue: false hasContentIssue false
  • English
  • Français

Determination of LC and LB

Published online by Cambridge University Press:  30 March 2016

T. Fukushima
T. Fukushima*
Affiliation:
National Astronomical Observatory 2-21-1, Ohsawa, Mitaka, Tokyo 181;JAPAN(Internet)toshio@spacetime.mtk.nao.ac.jp

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The location-independent part of TCB-TCG, the difference between the two new time scales adopted by the IAU (1992), was integrated numerically for three JPL planetary/lunar ephemerides; DE102, DE200, and DE245. The differences among these three integrations were mostly explained by the difference in the adopted constants of the ephemerides. It was shown that the post-Newtonian correction and the perturbation by asteroids are negligible except for the mean rate, LC. The comparison of these numerical integrations with the analytical formulas of Hirayama et al. (1987) and Fairhead and Bretagnon (1990) as well as their extended versions lead to the best estimate of LC as

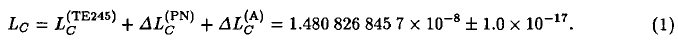
Combining this with the recent value of the geoid potential in Bursa et al. (1992), we estimated the value of LB, the scale difference between TCB and TT, as

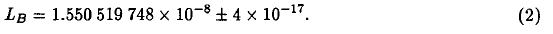
Table I summarizes these conclusions. These estimates of LC and LB are more reliable than the former values we gave (Fukushima et al. 1986). The new estimate of LB will be useful in converting the numerical values of some precisely determined astronomical constants such as AU measured in meter from those in TDB to those in TCB. Also the numerically integrated TCB-TCG, which are to be called Time Ephemeris, will be useful when converting between TCB and TDB, i.e. the time scales themselves. The full paper will be appeared in A & A with the title of Time Ephemeris.

Type
II. Joint Discussions
Information
Highlights of Astronomy , Volume 10: Highlights of Astronomy. As presented at the XXIInd General Assembly of the IAU, 1994 , 1995 , pp. 205
Copyright
Copyright © Kluwer 1995

References

Bursa, M., Sima, Z., Kostelecky, J., 1992, Studia geoph. et geod. 36, 101–114.CrossRefGoogle Scholar
Fairhead, L., Bretagnon, P., 1990, A & A 229, 240–247.Google Scholar
Fukushima, T., Fujimoto, M.-K., Kinoshita, H., Aoki, S., 1986, Celest. Mech. 36, 215–230.Google Scholar
Hirayama, Th., Fujimoto, M.-K., Kinoshita, H., Fukushima, T., 1987, Proc. IAG Symposia at IUGG XIX General Assembly, Tome I, 91–100.Google Scholar
IAU, 1992, Proc. 21st General Assembly, Transactions of the IAU, XXI, Kluwer Acad. Publ., Dordrecht.Google Scholar