Article contents
Entropy and martingales in Markov chain models
Published online by Cambridge University Press: 14 July 2016
Abstract
The concept of entropy in models is discussed with particular reference to the work of P.A.P. Moran. For a vector-valued Markov chain {Xk } whose states are relative-frequency (proportion) tables corresponding to a physical mixing model of a number N of particles over n urns, the definition of entropy may be based on the usual information-theoretic concept applied to the probability distribution given by the expectation 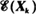 . The model is used for a brief probabilistic assessment of the relationship between Boltzmann's Η-Theorem, the Ehrenfest urn model, and Poincaré's considerations on the mixing of liquids and card shuffling, centred on the property of an ultimately uniform distribution of a single particle. It is then generalized to the situation where the total number of particles fluctuates over time, and martingale results are used to establish convergence for
. The model is used for a brief probabilistic assessment of the relationship between Boltzmann's Η-Theorem, the Ehrenfest urn model, and Poincaré's considerations on the mixing of liquids and card shuffling, centred on the property of an ultimately uniform distribution of a single particle. It is then generalized to the situation where the total number of particles fluctuates over time, and martingale results are used to establish convergence for 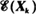 .
.
Information
- Type
- Part 6 — Stochastic Processes
- Information
- Copyright
- Copyright © 1982 Applied Probability Trust
References
- 4
- Cited by

