Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-05T04:16:00.643Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit theorems for sums of a sequence of random variables defined on a Markov chain

Published online by Cambridge University Press:  14 July 2016

David B. Wolfson
David B. Wolfson*
Affiliation:
McGill University, Montreal
Get access Rights & Permissions [Opens in a new window]

Abstract

Let {(Jn, Xn), n ≧ 0} be the standard J–X process of Markov renewal theory. Suppose {Jn, n ≧ 0} is irreducible, aperiodic and positive recurrent. It is shown using the strong mixing condition, that if 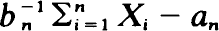converges in distribution, where an, bn > 0 (bn → ∞) are real constants, then the limit law F must be stable. Suppose Q(x) = {PijHi(x)} is the semi-Markov matrix of {(JnXn), n ≧ 0}. Then the n-fold convolution, Q∗n(bnx + anbn), converges in distribution to F(x)Π if and only if 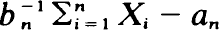converges in distribution to F. Π is the matrix of stationary transition probabilities of {Jn, n ≧ 0}. Sufficient conditions on the Hi's are given for the convergence of the sequence of semi-Markov matrices to F(x)Π, where F is stable.

Keywords

STABLE LAWSSEMI-MARKOV PROCESSESSTRONG MIXING CONDITION
Type
Short Communications
Information
Journal of Applied Probability , Volume 14 , Issue 3 , September 1977 , pp. 614 - 620
Copyright
Copyright © Applied Probability Trust 1977 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Chung, K. L. (1972) A Course in Probability Theory. Academic Press, New York.Google Scholar
[2] Fabens, A. J. and Neuts, M. F. (1970) The limiting distribution of the maximum term in a sequence of random variables defined on a Markov chain. J. Appl. Prob. 7, 754–760.CrossRefGoogle Scholar
[3] Gnedenko, B. V. and Kolmogorov, A. N. (1954) Limit Distributions for Sums of Independent Random Variables. Addison-Wesley, Reading, Mass.Google Scholar
[4] Ibragimov, I. A. (1962) Some limit theorems for stationary processes. Theor. Prob. Appl. 7, 349–382.CrossRefGoogle Scholar
[5] Loève, M. (1963) Probability Theory. Van Nostrand, Princeton, New Jersey.Google Scholar
[6] O'Brien, G. L. (1974) Limit theorems for sums of chain dependent processes. J. Appl. Prob. 11, 582–587.CrossRefGoogle Scholar
[7] Ortega, J. ?. (1972) Numerical Analysis. A Second Course. Academic Press, New York.Google Scholar
[8] Ott, T. (1973) Infinite divisibility and stability of finite semi-Markov matrices. University of Rochester Report CSS 73–11, 31 July 1973.Google Scholar
[9] Resnick, S. I. and Neuts, M. F. (1970) Limit laws for maximum of a sequence of random variables defined on a Markov chain. Adv. Appl. Prob. 2, 323–343.CrossRefGoogle Scholar
[10] Serfozo, R. F. (1973) Weak convergence of superpositions of randomly selected partial sums. Ann. Prob. 1, 1044–1056.CrossRefGoogle Scholar
[11] Tucker, H. (1968) Convolutions of distributions attracted to stable laws. Ann. Math. Statist. 39, 1381–1390.CrossRefGoogle Scholar