Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Astrauskas, A.
2006.
Strong laws for exponential order statistics and spacings.
Lithuanian Mathematical Journal,
Vol. 46,
Issue. 4,
p.
385.
Yatracos, Yannis G.
2009.
The asymptotic distribution of a cluster-index for i.i.d. normal random variables.
The Annals of Applied Probability,
Vol. 19,
Issue. 2,
González Cázares, Jorge
and
Ivanovs, Jevgenijs
2021.
Recovering Brownian and jump parts from high-frequency observations of a Lévy process.
Bernoulli,
Vol. 27,
Issue. 4,
Bibinger, Markus
2024.
Probabilistic Models and Statistics for Electronic Financial Markets in the Digital Age.
Jahresbericht der Deutschen Mathematiker-Vereinigung,
Vol. 126,
Issue. 3,
p.
129.

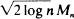 and show that
and show that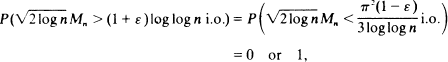 according to whether ε> 0 or
according to whether ε> 0 or 