Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Afanas’ev, V. I.
1979.
A Conditional Random Walk with a Negative Drift.
Theory of Probability & Its Applications,
Vol. 24,
Issue. 1,
p.
192.
Asmussen, Søren
1982.
Conditioned limit theorems relating a random walk to its associate, with applications to risk reserve processes and the GI/G/1 queue.
Advances in Applied Probability,
Vol. 14,
Issue. 01,
p.
143.
Hooghiemstra, G.
1983.
Conditioned limit theorems for waiting-time processes of the M/G/1 queue.
Journal of Applied Probability,
Vol. 20,
Issue. 03,
p.
675.
Glynn, Peter W.
1990.
Stochastic Models.
Vol. 2,
Issue. ,
p.
145.
Dembo, Amir
and
Karlin, Samuel
1993.
Central limit theorems of partial sums for large segmental values.
Stochastic Processes and their Applications,
Vol. 45,
Issue. 2,
p.
259.
Stadje, Wolfgang
1994.
On the behavior of the batch arrival queueMx/M/1 during a busy period.
Naval Research Logistics,
Vol. 41,
Issue. 2,
p.
153.
Kijima, Masaaki
and
Makimoto, Naoki
1999.
Applied Probability and Stochastic Processes.
Vol. 19,
Issue. ,
p.
277.
Fleischmann, Klaus
and
Vatutin, Vladimir A.
1999.
Reduced subcritical Galton-Watson processes in a random environment.
Advances in Applied Probability,
Vol. 31,
Issue. 01,
p.
88.
Chernyak, Vladimir Y.
Chertkov, Michael
Goldberg, David A.
and
Turitsyn, Konstantin
2010.
Non-Equilibrium Statistical Physics of Currents in Queuing Networks.
Journal of Statistical Physics,
Vol. 140,
Issue. 5,
p.
819.
Schwerdtfeger, Uwe
2014.
Linear functional equations with a catalytic variable and area limit laws for lattice paths and polygons.
European Journal of Combinatorics,
Vol. 36,
Issue. ,
p.
608.

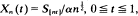 where
where 