Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Comets, Francis
Delarue, François
and
Schott, René
2007.
Distributed algorithms in an ergodic Markovian environment.
Random Structures & Algorithms,
Vol. 30,
Issue. 1-2,
p.
131.
Delarue, F.
2008.
Hitting time of a corner for a reflected diffusion in the square.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 44,
Issue. 5,
Löcherbach, Eva
Loukianova, Dasha
and
Loukianov, Oleg
2011.
Polynomial bounds in the Ergodic theorem for one-dimensional diffusions and integrability of hitting times.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 47,
Issue. 2,
Löcherbach, Eva
Loukianov, Oleg
and
Loukianova, Dasha
2014.
Spectral condition, hitting times and Nash inequality.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 50,
Issue. 4,
Menshikov, Mikhail V.
Mijatović, Aleksandar
and
Wade, Andrew R.
2021.
In and Out of Equilibrium 3: Celebrating Vladas Sidoravicius.
Vol. 77,
Issue. ,
p.
637.

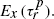 As an application we exhibit classes of diffusion processes which are recurrent but
As an application we exhibit classes of diffusion processes which are recurrent but 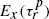 is infinite for all
is infinite for all 