Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Halverson, D.R.
and
Wise, G.L.
1981.
Asymptotic memoryless detection of random signals in dependent noise.
Journal of the Franklin Institute,
Vol. 312,
Issue. 1,
p.
13.
Bradley, Richard C
1981.
Central limit theorems under weak dependence.
Journal of Multivariate Analysis,
Vol. 11,
Issue. 1,
p.
1.
Bradley, Richard C
1983.
Equivalent measures of dependence.
Journal of Multivariate Analysis,
Vol. 13,
Issue. 1,
p.
167.
Denker, Manfred
Goldie, C. M.
and
Morrow, G. J.
1986.
Dependence in Probability and Statistics.
p.
269.
Peligrad, Magda
1986.
Invariance principles under weak dependence.
Journal of Multivariate Analysis,
Vol. 19,
Issue. 2,
p.
299.
Peligrad, Magda
1986.
Dependence in Probability and Statistics.
p.
193.
Bradely, Richard C.
1988.
On a theorem of gordin.
Stochastics,
Vol. 24,
Issue. 4,
p.
357.
Jakubowski, Adam
1993.
Minimal conditions in p-stable limit theorems.
Stochastic Processes and their Applications,
Vol. 44,
Issue. 2,
p.
291.
Sunklodas, J.
2000.
Limit Theorems of Probability Theory.
p.
113.
Bryc, Włodzimierz
and
Kaftal, Victor
2003.
Strong mixing coefficients for non-commutative Gaussian processes.
Proceedings of the American Mathematical Society,
Vol. 132,
Issue. 2,
p.
523.
BRADLEY, RICHARD C.
2012.
ON THE SPECTRAL MEASURES OF SOME WEAKLY STATIONARY SEQUENCES INVOLVING RANDOMLY SPACED OBSERVATIONS.
Stochastics and Dynamics,
Vol. 12,
Issue. 01,
p.
1150004.
Bradley, Richard C.
2014.
On a ‘Replicating Character String’ Model.
Journal of Applied Probability,
Vol. 51,
Issue. 2,
p.
512.
Bradley, Richard C.
2014.
On a ‘Replicating Character String’ Model.
Journal of Applied Probability,
Vol. 51,
Issue. 02,
p.
512.
Janson, Svante
2015.
On degenerate sums of m-dependent variables.
Journal of Applied Probability,
Vol. 52,
Issue. 04,
p.
1146.
Janson, Svante
2015.
On degenerate sums of m-dependent variables.
Journal of Applied Probability,
Vol. 52,
Issue. 4,
p.
1146.
Tempelman, Arkady
2022.
Randomized multivariate Central Limit Theorems for ergodic homogeneous random fields.
Stochastic Processes and their Applications,
Vol. 143,
Issue. ,
p.
89.
Davydov, Youri
and
Tempelman, Arkady
2024.
Randomized limit theorems for stationary ergodic random processes and fields.
Stochastic Processes and their Applications,
Vol. 174,
Issue. ,
p.
104380.

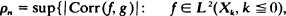
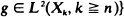 . Here an example of {
. Here an example of {