Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T06:23:29.100Z Has data issue: false hasContentIssue false
  • English
  • Français

Rough limit results for level-crossing probabilities

Part of: Limit theorems Stochastic processes

Published online by Cambridge University Press:  14 July 2016

Harri Nyrhinen
Harri Nyrhinen*
Affiliation:
Pohjola Insurance Company Ltd.
*
∗ Postal address: Pohjola Insurance Company Ltd., Lapinmäentie 1, 00013 Pohjola, Finland.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Y1, Y2, · ·· be a stochastic process and M a positive real number. Define TM = inf{n | Yn > M} (TM = + ∞ if 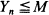for n = 1, 2, ···)· We are interested in the probabilities P(TM <∞) and in particular in the case when these tend to zero exponentially fast when M tends to infinity. The techniques of large deviations theory are used to obtain conditions for this and to find out the rate of convergence. The main hypotheses required are given in terms of the generating functions associated with the process (Yn).

Keywords

LARGE DEVIATIONS THEORYINSURANCE MATHEMATICS

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory
Secondary: 60F10: Large deviations
Type
Research Papers
Information
Journal of Applied Probability , Volume 31 , Issue 2 , June 1994 , pp. 373 - 382
Copyright
Copyright © Applied Probability Trust 1994 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The main part of this paper was written during a research project in the Rolf Nevanlinna Institute with the support of the Foundation for the Promotion of the Actuarial Profession.

References

[1] Arndt, K. (1980) Asymptotic properties of the distribution of the supremum of a random walk on a Markov chain. Theory Prob. Appl. 2, 309–324.Google Scholar
[2] Asmussen, S. (1989) Risk theory in a Markovian environment. Scand. Actuarial J., 69–100.Google Scholar
[3] Björk, T. and Grandell, J. (1988) Exponential inequalities for ruin probabilities in the Cox case. Scand. Actuarial J., 77–111.Google Scholar
[4] Cramér, H. (1955) Collective risk theory. Jubilee Volume of Försäkringsbolaget Skandia, Stockholm.Google Scholar
[5] Ellis, R. S. (1984) Large deviations for a general class of random vectors. Ann. Prob. 12, 1–12.CrossRefGoogle Scholar
[6] Ellis, R. S. (1985) Entropy, Large Deviations and Statistical Mechanics. Springer-Verlag, New York.Google Scholar
[7] Gerber, H. (1982) Ruin theory in the linear model. Insurance: Mathematics and Economics 1, 177–184.Google Scholar
[8] Iscoe, I., Ney, P. and Nummelin, E. (1985) Large deviations of uniformly recurrent Markov additive processes. Adv. Appl. Math. 6, 373–412.CrossRefGoogle Scholar
[9] Lehtonen, T. and Nyrhinen, H. (1992) Simulating level crossing probabilities by importance sampling. Adv. Appl. Prob. 24, 858–874.CrossRefGoogle Scholar
[10] Lehtonen, T. and Nyrhinen, H. (1992) On asymptotically efficient simulation of ruin probabilities in a Markovian environment. Scand. Actuarial J. , 60–75.Google Scholar
[11] Martin-Löf, A. (1983) Entropy estimates for ruin probabilities. In Probability and Mathematical Statistics, ed. Gut, A. and Holst, L., Dept, of Mathematics, Uppsala University, 129–139.Google Scholar
[12] Nummelin, E. (1986) Lecture Series on Large Deviations Theory. Helsinki University.Google Scholar
[13] Rockafellar, R. T. (1970) Convex Analysis. Princeton University Press.Google Scholar