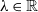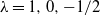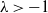1. Introduction
Consider the setting of a multinomial goodness-of-fit test, with n independent trials in which each trial leads to a unique classification over
![]() $r\geq2$
classes. Let
$r\geq2$
classes. Let
![]() $U_1,\ldots,U_r$
represent the observed frequencies arising in each class, and denote the non-zero classification probabilities by
$U_1,\ldots,U_r$
represent the observed frequencies arising in each class, and denote the non-zero classification probabilities by
![]() $\boldsymbol{p}=(p_1,\ldots,p_r)$
. In 1984, Cressie and Read [Reference Cressie and Read7] introduced the power divergence family of statistics for testing the null hypothesis
$\boldsymbol{p}=(p_1,\ldots,p_r)$
. In 1984, Cressie and Read [Reference Cressie and Read7] introduced the power divergence family of statistics for testing the null hypothesis
![]() $H_0$
:
$H_0$
:
![]() $\boldsymbol{p}=\boldsymbol{p}_0$
against the alternative hypothesis
$\boldsymbol{p}=\boldsymbol{p}_0$
against the alternative hypothesis
![]() $H_1$
:
$H_1$
:
![]() $\boldsymbol{p}=\boldsymbol{p}_1$
. These statistics are given by
$\boldsymbol{p}=\boldsymbol{p}_1$
. These statistics are given by
 \begin{equation} T_\lambda=\frac{2}{\lambda(\lambda+1)}\sum_{j=1}^rU_j\bigg[\bigg(\frac{U_j}{np_j}\bigg)^\lambda-1\bigg],\end{equation}
\begin{equation} T_\lambda=\frac{2}{\lambda(\lambda+1)}\sum_{j=1}^rU_j\bigg[\bigg(\frac{U_j}{np_j}\bigg)^\lambda-1\bigg],\end{equation}
where the index parameter
![]() $\lambda\in\mathbb{R}$
. Here, and throughout the paper, we assume the validity of the null hypothesis, and, for ease of notation, suppress the subscript in the notation
$\lambda\in\mathbb{R}$
. Here, and throughout the paper, we assume the validity of the null hypothesis, and, for ease of notation, suppress the subscript in the notation
![]() $\boldsymbol{p}_0$
. Note that
$\boldsymbol{p}_0$
. Note that
![]() $\sum_{j=1}^rU_j=n$
and
$\sum_{j=1}^rU_j=n$
and
![]() $\sum_{j=1}^rp_j=1$
.
$\sum_{j=1}^rp_j=1$
.
When
![]() $\lambda=0,-1$
, the notation in (1) should be understood as a result of passage to the limit, in which cases we recover the log-likelihood ratio and modified log likelihood ratio statistics, respectively:
$\lambda=0,-1$
, the notation in (1) should be understood as a result of passage to the limit, in which cases we recover the log-likelihood ratio and modified log likelihood ratio statistics, respectively:
 \begin{align} L = 2\sum_{j=1}^r U_j\log\!\bigg(\frac{U_j}{np_j}\bigg), \qquad GM^2 = 2n\sum_{j=1}^r p_j\log\!\bigg(\frac{np_j}{U_j}\bigg).\end{align}
\begin{align} L = 2\sum_{j=1}^r U_j\log\!\bigg(\frac{U_j}{np_j}\bigg), \qquad GM^2 = 2n\sum_{j=1}^r p_j\log\!\bigg(\frac{np_j}{U_j}\bigg).\end{align}
The cases
![]() $\lambda=1,-1/2$
correspond to Pearson’s chi-square statistic [Reference Pearson25] and the Freeman–Tukey statistic [Reference Freeman and Tukey10], given by
$\lambda=1,-1/2$
correspond to Pearson’s chi-square statistic [Reference Pearson25] and the Freeman–Tukey statistic [Reference Freeman and Tukey10], given by
 \begin{align} \chi^2 = \sum_{j=1}^r \frac{(U_j - n p_j)^2}{n p_j}, \qquad T^2 = 4\sum_{j=1}^r\big(\sqrt{U_j}-\sqrt{np_j}\big)^2.\end{align}
\begin{align} \chi^2 = \sum_{j=1}^r \frac{(U_j - n p_j)^2}{n p_j}, \qquad T^2 = 4\sum_{j=1}^r\big(\sqrt{U_j}-\sqrt{np_j}\big)^2.\end{align}
The power divergence family of statistics can therefore be seen to unify several commonly used goodness-of-fit tests. The statistic
![]() $T_{2/3}$
, often referred to as the Cressie–Read statistic, was also suggested in [Reference Cressie and Read7, Reference Read and Cressie32] as a good alternative to the classical likelihood ratio and Pearson statistics.
$T_{2/3}$
, often referred to as the Cressie–Read statistic, was also suggested in [Reference Cressie and Read7, Reference Read and Cressie32] as a good alternative to the classical likelihood ratio and Pearson statistics.
A fundamental result is that, for all
![]() $\lambda\in\mathbb{R}$
, the statistic
$\lambda\in\mathbb{R}$
, the statistic
![]() $T_\lambda$
converges in distribution to the
$T_\lambda$
converges in distribution to the
![]() $\chi_{(r-1)}^2$
distribution as the number of trials n tends to infinity [Reference Cressie and Read7, p. 443]. However, in practice we have a finite sample, and so it is of interest to assess the quality of this distributional approximation for finite n. In the literature, this has been done on the one hand through theoretical bounds on the rate of convergence, which will be the focus of this paper, and on the other through simulation studies. The findings of simulation studies from the literature are briefly reviewed in Remark 4, in which we also discuss how the theoretical bounds obtained in this paper reflect the findings of these studies.
$\chi_{(r-1)}^2$
distribution as the number of trials n tends to infinity [Reference Cressie and Read7, p. 443]. However, in practice we have a finite sample, and so it is of interest to assess the quality of this distributional approximation for finite n. In the literature, this has been done on the one hand through theoretical bounds on the rate of convergence, which will be the focus of this paper, and on the other through simulation studies. The findings of simulation studies from the literature are briefly reviewed in Remark 4, in which we also discuss how the theoretical bounds obtained in this paper reflect the findings of these studies.
From the theoretical literature, the quality of the chi-square approximation of the distibution of the statistic
![]() $T_{\lambda}$
has been assessed by Edgeworth expansions [Reference Assylebekov3, Reference Assylebekov, Zubov and Ulyanov4, Reference Fujikoshi and Ulyanov11, Reference Prokhorov and Ulyanov29, Reference Read31, Reference Ulyanov and Zubov37]. In [Reference Read31], Edgeworth expansions were used to propose closer approximations to the distribution function of
$T_{\lambda}$
has been assessed by Edgeworth expansions [Reference Assylebekov3, Reference Assylebekov, Zubov and Ulyanov4, Reference Fujikoshi and Ulyanov11, Reference Prokhorov and Ulyanov29, Reference Read31, Reference Ulyanov and Zubov37]. In [Reference Read31], Edgeworth expansions were used to propose closer approximations to the distribution function of
![]() $T_{\lambda}$
that are of the form of the
$T_{\lambda}$
that are of the form of the
![]() $\chi_{(r-1)}^2$
distribution function plus an o(1) correction. The work of [Reference Read31] generalised results of [Reference Siotani and Fujikoshi34] that had been given for the Pearson, likelihood ratio, and Freeman–Tukey statistics (
$\chi_{(r-1)}^2$
distribution function plus an o(1) correction. The work of [Reference Read31] generalised results of [Reference Siotani and Fujikoshi34] that had been given for the Pearson, likelihood ratio, and Freeman–Tukey statistics (
![]() $\lambda=1,0,-1/2$
). However, as noted in [Reference Prokhorov and Ulyanov29], it is impossible to determine a rate of convergence from the expansions given in [Reference Read31, Reference Siotani and Fujikoshi34]. Bounds on the rate of convergence of the distribution of
$\lambda=1,0,-1/2$
). However, as noted in [Reference Prokhorov and Ulyanov29], it is impossible to determine a rate of convergence from the expansions given in [Reference Read31, Reference Siotani and Fujikoshi34]. Bounds on the rate of convergence of the distribution of
![]() $T_\lambda$
to its limiting
$T_\lambda$
to its limiting
![]() $\chi_{(r-1)}^2$
distribution via Edgeworth expansions were obtained in [Reference Fujikoshi and Ulyanov11, Reference Prokhorov and Ulyanov29]. For
$\chi_{(r-1)}^2$
distribution via Edgeworth expansions were obtained in [Reference Fujikoshi and Ulyanov11, Reference Prokhorov and Ulyanov29]. For
![]() $r\geq4$
, [Reference Ulyanov and Zubov37] obtained an
$r\geq4$
, [Reference Ulyanov and Zubov37] obtained an
![]() $O(n^{-(r-1)/r})$
bound on the rate of convergence in the Kolmogorov distance (see also [Reference Assylebekov3] for a refinement of this result) and, for
$O(n^{-(r-1)/r})$
bound on the rate of convergence in the Kolmogorov distance (see also [Reference Assylebekov3] for a refinement of this result) and, for
![]() $r=3$
, [Reference Assylebekov, Zubov and Ulyanov4] obtained an
$r=3$
, [Reference Assylebekov, Zubov and Ulyanov4] obtained an
![]() $O(n^{-3/4+0.065})$
bound on the rate of convergence in the same metric, with both bounds holding for all
$O(n^{-3/4+0.065})$
bound on the rate of convergence in the same metric, with both bounds holding for all
![]() $\lambda\in\mathbb{R}$
.
$\lambda\in\mathbb{R}$
.
Bounds on the rate of convergence have also been given for special cases of the power divergence family. For the likelihood ratio statistic, [Reference Anastasiou and Reinert2] recently used Stein’s method to obtain an explicit
![]() $O(n^{-1/2})$
bound for smooth test functions. It is worth noting that the setting of [Reference Anastasiou and Reinert2] was more general than the categorical data setting of this paper. For Pearson’s statistic, it was shown in [Reference Yarnold38] using Edgeworth expansions that a bound on the rate of convergence of Pearson’s statistic in the Kolmogorov distance is
$O(n^{-1/2})$
bound for smooth test functions. It is worth noting that the setting of [Reference Anastasiou and Reinert2] was more general than the categorical data setting of this paper. For Pearson’s statistic, it was shown in [Reference Yarnold38] using Edgeworth expansions that a bound on the rate of convergence of Pearson’s statistic in the Kolmogorov distance is
![]() $O(n^{-(r-1)/r})$
for
$O(n^{-(r-1)/r})$
for
![]() $r\geq2$
, which was improved by [Reference Götze and Ulyanov17] to
$r\geq2$
, which was improved by [Reference Götze and Ulyanov17] to
![]() $O(n^{-1})$
for
$O(n^{-1})$
for
![]() $r\geq6$
. An explicit
$r\geq6$
. An explicit
![]() $O(n^{-1/2})$
Kolmogorov distance bound was obtained by Stein’s method in [Reference Mann22]. Recently, [Reference Gaunt, Pickett and Reinert14] used Stein’s method to obtain explicit error bounds for Pearson’s statistic, measured using smooth test functions. These bounds will be needed in the following, and are recorded here.
$O(n^{-1/2})$
Kolmogorov distance bound was obtained by Stein’s method in [Reference Mann22]. Recently, [Reference Gaunt, Pickett and Reinert14] used Stein’s method to obtain explicit error bounds for Pearson’s statistic, measured using smooth test functions. These bounds will be needed in the following, and are recorded here.
Let
![]() $C_b^k(\mathbb{R}^+)$
denote the class of bounded functions
$C_b^k(\mathbb{R}^+)$
denote the class of bounded functions
![]() $h \,:\, \mathbb{R}^+\rightarrow\mathbb{R}$
for which
$h \,:\, \mathbb{R}^+\rightarrow\mathbb{R}$
for which
![]() $h^{(k)}$
exists and derivatives up to kth order are bounded. Let
$h^{(k)}$
exists and derivatives up to kth order are bounded. Let
![]() $r\geq2$
and
$r\geq2$
and
![]() $p_*\,:\!=\,\min_{1\leq j\leq r}p_j$
. Suppose
$p_*\,:\!=\,\min_{1\leq j\leq r}p_j$
. Suppose
![]() $np_*\geq 1$
. Then, the following bounds were obtained in [Reference Gaunt, Pickett and Reinert14]. For
$np_*\geq 1$
. Then, the following bounds were obtained in [Reference Gaunt, Pickett and Reinert14]. For
![]() $h \in C_b^5(\mathbb{R}^+)$
,
$h \in C_b^5(\mathbb{R}^+)$
,
 \begin{align}\big|\mathbb{E} [h(\chi^2)] - \chi^2_{(r-1)} h \big| &\leq \frac{4}{(r+1)n}\bigg(\!\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}\bigg)^2\big\{19\|h\|+366\|h^{\prime}\|+2016\|h^{\prime\prime}\|\nonumber\\&\quad+5264\|h^{(3)}\|+106\,965\|h^{(4)}\|+302\,922\|h^{(5)}\|\big\},\end{align}
\begin{align}\big|\mathbb{E} [h(\chi^2)] - \chi^2_{(r-1)} h \big| &\leq \frac{4}{(r+1)n}\bigg(\!\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}\bigg)^2\big\{19\|h\|+366\|h^{\prime}\|+2016\|h^{\prime\prime}\|\nonumber\\&\quad+5264\|h^{(3)}\|+106\,965\|h^{(4)}\|+302\,922\|h^{(5)}\|\big\},\end{align}
and, for
![]() $h \in C_b^2(\mathbb{R}^+)$
,
$h \in C_b^2(\mathbb{R}^+)$
,
 \begin{equation}\big|\mathbb{E} [h(\chi^2)] - \chi^2_{(r-1)} h \big| \leq \frac{24}{(r+1)\sqrt{n}\,}\big\{3\|h\|+23\|h^{\prime}\|+42\|h^{\prime\prime}\|\big\}\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,},\end{equation}
\begin{equation}\big|\mathbb{E} [h(\chi^2)] - \chi^2_{(r-1)} h \big| \leq \frac{24}{(r+1)\sqrt{n}\,}\big\{3\|h\|+23\|h^{\prime}\|+42\|h^{\prime\prime}\|\big\}\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,},\end{equation}
where
![]() $\chi_{(r-1)}^2h$
denotes the expectation
$\chi_{(r-1)}^2h$
denotes the expectation
![]() $\mathbb{E}[h(Y_{r-1})]$
for
$\mathbb{E}[h(Y_{r-1})]$
for
![]() $Y_{r-1}\sim \chi_{(r-1)}^2$
. Here and throughout the paper, we write
$Y_{r-1}\sim \chi_{(r-1)}^2$
. Here and throughout the paper, we write
![]() $\|\cdot\|$
for the usual supremum norm
$\|\cdot\|$
for the usual supremum norm
![]() $\|\cdot\|_\infty$
of a real-valued function. The bound in (4) achieves the optimal
$\|\cdot\|_\infty$
of a real-valued function. The bound in (4) achieves the optimal
![]() $O(n^{-1})$
rate, although when the constants are large compared to n the bound in (5) may give the smaller numerical bound. Both bounds (4) and (5) have an optimal dependence on
$O(n^{-1})$
rate, although when the constants are large compared to n the bound in (5) may give the smaller numerical bound. Both bounds (4) and (5) have an optimal dependence on
![]() $p_*$
, since, for a fixed number of classes r, both bounds tend to zero if and only if
$p_*$
, since, for a fixed number of classes r, both bounds tend to zero if and only if
![]() $np_*\rightarrow\infty$
, which is precisely the condition under which
$np_*\rightarrow\infty$
, which is precisely the condition under which
![]() $\chi^2\rightarrow_\mathrm{d} \chi_{(r-1)}^2$
(see [Reference Greenwood and Nikulin18]). The bounds (4) and (5) are the first in the literature on Pearson’s statistic to decay to zero if and only if
$\chi^2\rightarrow_\mathrm{d} \chi_{(r-1)}^2$
(see [Reference Greenwood and Nikulin18]). The bounds (4) and (5) are the first in the literature on Pearson’s statistic to decay to zero if and only if
![]() $np_*\rightarrow\infty$
, and in the case of (4) achieve the optimal
$np_*\rightarrow\infty$
, and in the case of (4) achieve the optimal
![]() $O(n^{-1})$
rate for all
$O(n^{-1})$
rate for all
![]() $r\geq2$
.
$r\geq2$
.
In this paper, we generalise the bounds of [Reference Gaunt, Pickett and Reinert14] to the family of power divergence statistics
![]() $T_\lambda$
,
$T_\lambda$
,
![]() $\lambda>-1$
, the largest subclass of the power divergence family for which finite-sample bounds can be given when measured using smooth test functions, as in (4) and (5). Indeed, it can be seen from (1) and (2) that, for
$\lambda>-1$
, the largest subclass of the power divergence family for which finite-sample bounds can be given when measured using smooth test functions, as in (4) and (5). Indeed, it can be seen from (1) and (2) that, for
![]() $\lambda\leq-1$
, we have
$\lambda\leq-1$
, we have
![]() $T_\lambda=\infty$
if any of the observed frequencies
$T_\lambda=\infty$
if any of the observed frequencies
![]() $U_1,\ldots,U_r$
are zero, meaning that the expectation
$U_1,\ldots,U_r$
are zero, meaning that the expectation
![]() $\mathbb{E}[h(T_\lambda)]$
is undefined. The bounds in Theorem 2 are of the optimal
$\mathbb{E}[h(T_\lambda)]$
is undefined. The bounds in Theorem 2 are of the optimal
![]() $n^{-1}$
order. Specialising to the case
$n^{-1}$
order. Specialising to the case
![]() $\lambda=0$
of the likelihood ratio statistic, our
$\lambda=0$
of the likelihood ratio statistic, our
![]() $O(n^{-1})$
bound improves on the
$O(n^{-1})$
bound improves on the
![]() $O(n^{-1/2})$
rate (and has a better dependence on the other model parameters) of [Reference Anastasiou and Reinert2] that was given in a more general setting than that of the categorical data considered in this paper. Our results also complement [Reference Gaunt and Reinert15] in which Stein’s method is used to obtain order
$O(n^{-1/2})$
rate (and has a better dependence on the other model parameters) of [Reference Anastasiou and Reinert2] that was given in a more general setting than that of the categorical data considered in this paper. Our results also complement [Reference Gaunt and Reinert15] in which Stein’s method is used to obtain order
![]() $O(n^{-1})$
bounds for the chi-square approximation of Friedman’s statistic. In Theorem 3, we provide suboptimal
$O(n^{-1})$
bounds for the chi-square approximation of Friedman’s statistic. In Theorem 3, we provide suboptimal
![]() $O(n^{-1/2})$
bounds which may yield smaller numerical bounds for small sample sizes n.
$O(n^{-1/2})$
bounds which may yield smaller numerical bounds for small sample sizes n.
Like the bounds of [Reference Gaunt, Pickett and Reinert14] for Pearson’s statistic, for all fixed
![]() $\lambda>-1$
and
$\lambda>-1$
and
![]() $r\geq2$
, the bounds of Theorems 2 and 3 enjoy the property of decaying to zero if and only if
$r\geq2$
, the bounds of Theorems 2 and 3 enjoy the property of decaying to zero if and only if
![]() $np_*\rightarrow\infty$
. If
$np_*\rightarrow\infty$
. If
![]() $r\geq2$
is fixed and we allow
$r\geq2$
is fixed and we allow
![]() $\lambda$
to vary with n, then the bounds of Theorems 2 and 3 tend to zero if and only if
$\lambda$
to vary with n, then the bounds of Theorems 2 and 3 tend to zero if and only if
![]() $np_*/\lambda^2\rightarrow\infty$
, which is again an optimal condition (see Remark 3). The dependence of our bounds on r is also respectable. The excellent dependence of the bounds of Theorem 3 on all parameters allows us to prescribe simple conditions under which the chi-square approximation is valid, when the quantities
$np_*/\lambda^2\rightarrow\infty$
, which is again an optimal condition (see Remark 3). The dependence of our bounds on r is also respectable. The excellent dependence of the bounds of Theorem 3 on all parameters allows us to prescribe simple conditions under which the chi-square approximation is valid, when the quantities
![]() $\lambda$
, r, and
$\lambda$
, r, and
![]() $p_1,\ldots,p_r$
may vary with n; see Remark 3. As already discussed, some of these conditions are optimal, and in parameter regimes in which we have not been able to obtain optimal conditions we conjecture what these optimal conditions are; see Remark 3, again.
$p_1,\ldots,p_r$
may vary with n; see Remark 3. As already discussed, some of these conditions are optimal, and in parameter regimes in which we have not been able to obtain optimal conditions we conjecture what these optimal conditions are; see Remark 3, again.
It is perhaps not a priori obvious that the
![]() $O(n^{-1})$
rate of our main bounds would hold for all power divergence statistics with
$O(n^{-1})$
rate of our main bounds would hold for all power divergence statistics with
![]() $\lambda>-1$
. For example, simulation studies have shown that for small samples n the likelihood ratio statistic (
$\lambda>-1$
. For example, simulation studies have shown that for small samples n the likelihood ratio statistic (
![]() $\lambda=0$
) is less accurate at approximating the limiting
$\lambda=0$
) is less accurate at approximating the limiting
![]() $\chi_{(r-1)}^2$
distribution than is Pearson’s statistic (
$\chi_{(r-1)}^2$
distribution than is Pearson’s statistic (
![]() $\lambda=1$
; see, for example, [Reference Chapman5, Reference Larantz20]). Our results show, however, that at least when measured using smooth test functions, the actual rate of convergence is the same for large n if the number of classes r is fixed. If the number of classes r is allowed to grow with n, then Pearson’s statistic will converge faster, though (see Remark 3). It is also important to note that our assumption of smooth test functions is essential for the purpose of obtaining
$\lambda=1$
; see, for example, [Reference Chapman5, Reference Larantz20]). Our results show, however, that at least when measured using smooth test functions, the actual rate of convergence is the same for large n if the number of classes r is fixed. If the number of classes r is allowed to grow with n, then Pearson’s statistic will converge faster, though (see Remark 3). It is also important to note that our assumption of smooth test functions is essential for the purpose of obtaining
![]() $O(n^{-1})$
convergence rates that hold for all
$O(n^{-1})$
convergence rates that hold for all
![]() $r\geq2$
and all
$r\geq2$
and all
![]() $\lambda>-1$
. For example, in the case
$\lambda>-1$
. For example, in the case
![]() $r=3$
, convergence rates in the Kolmogorov metric can be no faster than
$r=3$
, convergence rates in the Kolmogorov metric can be no faster than
![]() $O(n^{-3/4}\log\log n)$
; see [Reference Assylebekov, Zubov and Ulyanov4, Remark 3].
$O(n^{-3/4}\log\log n)$
; see [Reference Assylebekov, Zubov and Ulyanov4, Remark 3].
The rest of the paper is organised as follows. In Section 2 we state our main results. Theorem 1 provides analogues of the bounds (4) and (5) for Pearson’s statistic that hold for wider classes of test functions at the expense of a worse dependence on the parameter r. Our main result, Theorem 2, provides
![]() $O(n^{-1})$
bounds to quantify the chi-square approximation of the power divergence statistics. Alternative
$O(n^{-1})$
bounds to quantify the chi-square approximation of the power divergence statistics. Alternative
![]() $O(n^{-1/2})$
bounds are given in Theorem 3, and from one of these bounds we extract a Kolmogorov distance bound (Corollary 1). We end Section 2 with several remarks discussing the bounds. In Section 3, we present several preliminary lemmas that are needed for the proofs of our main results. We prove the main results in Section 4. In Appendix A we present some basics of Stein’s method for chi-square approximation and use it to give a short proof of Theorem 1. Finally, in Appendix B we prove a technical lemma from Section 3.
$O(n^{-1/2})$
bounds are given in Theorem 3, and from one of these bounds we extract a Kolmogorov distance bound (Corollary 1). We end Section 2 with several remarks discussing the bounds. In Section 3, we present several preliminary lemmas that are needed for the proofs of our main results. We prove the main results in Section 4. In Appendix A we present some basics of Stein’s method for chi-square approximation and use it to give a short proof of Theorem 1. Finally, in Appendix B we prove a technical lemma from Section 3.
2. Main results
We first present a theorem which complements the main result of [Reference Gaunt, Pickett and Reinert14] by giving explicit error bounds for the chi-square approximation of Pearson’s statistic that hold for larger classes of function than those used by [Reference Gaunt, Pickett and Reinert14]. The proof involves a minor modification of the proof of the bounds (4) and (5) of [Reference Gaunt, Pickett and Reinert14], and the details are given in Appendix A.
Before stating the theorem, we introduce some notation. We let
![]() $p_*\,:\!=\,\mathrm{min}_{1\leq j\leq r}p_j$
. Let
$p_*\,:\!=\,\mathrm{min}_{1\leq j\leq r}p_j$
. Let
![]() $C_b^{j,k}(\mathbb{R}^+)$
,
$C_b^{j,k}(\mathbb{R}^+)$
,
![]() $j\leq k$
, denote the class of functions
$j\leq k$
, denote the class of functions
![]() $h \,:\, \mathbb{R}^+\rightarrow\mathbb{R}$
for which
$h \,:\, \mathbb{R}^+\rightarrow\mathbb{R}$
for which
![]() $h^{(k)}$
exists and derivatives of order
$h^{(k)}$
exists and derivatives of order
![]() $j,j+1,\ldots,k$
are bounded. Note that
$j,j+1,\ldots,k$
are bounded. Note that
![]() $C_b^k(\mathbb{R}^+)\subset C_b^{j,k}(\mathbb{R}^+)$
for
$C_b^k(\mathbb{R}^+)\subset C_b^{j,k}(\mathbb{R}^+)$
for
![]() $j\geq1$
.
$j\geq1$
.
Theorem 1. Let
![]() $(U_1, \ldots, U_r)$
be the multinomial vector of n observed counts, where
$(U_1, \ldots, U_r)$
be the multinomial vector of n observed counts, where
![]() $r \geq 2$
, and suppose that
$r \geq 2$
, and suppose that
![]() $np_*\geq 1$
. Let
$np_*\geq 1$
. Let
![]() $\chi^2$
be Pearson’s chi-square statistic as defined in (3). Then, for
$\chi^2$
be Pearson’s chi-square statistic as defined in (3). Then, for
![]() $h\in C_b^{1,5}(\mathbb{R}^+)$
,
$h\in C_b^{1,5}(\mathbb{R}^+)$
,
 \begin{align} \big|\mathbb{E} [h(\chi^2)] - \chi^2_{(r-1)} h \big| & \leq \frac{1}{(r+1)^{1/2}n}\bigg(\!\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}\bigg)^2\bigg\{122\|h^{\prime}\|+1970\|h^{\prime\prime}\|\nonumber\\ &\quad+6943\|h^{(3)}\|+12\,731\|h^{(4)}\|+643\,710\|h^{(5)}\|\bigg\}, \end{align}
\begin{align} \big|\mathbb{E} [h(\chi^2)] - \chi^2_{(r-1)} h \big| & \leq \frac{1}{(r+1)^{1/2}n}\bigg(\!\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}\bigg)^2\bigg\{122\|h^{\prime}\|+1970\|h^{\prime\prime}\|\nonumber\\ &\quad+6943\|h^{(3)}\|+12\,731\|h^{(4)}\|+643\,710\|h^{(5)}\|\bigg\}, \end{align}
and, for
![]() $h\in C_b^{1,2}(\mathbb{R}^+)$
,
$h\in C_b^{1,2}(\mathbb{R}^+)$
,
 \begin{equation} \big|\mathbb{E} [h(\chi^2)] - \chi^2_{(r-1)} h \big| \leq \frac{1}{\sqrt{(r+1)n}\,}\big\{115\|h^{\prime}\|+536\|h^{\prime\prime}\|\big\}\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}. \end{equation}
\begin{equation} \big|\mathbb{E} [h(\chi^2)] - \chi^2_{(r-1)} h \big| \leq \frac{1}{\sqrt{(r+1)n}\,}\big\{115\|h^{\prime}\|+536\|h^{\prime\prime}\|\big\}\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}. \end{equation}
Also, for
![]() $h\in C_b^{2,5}(\mathbb{R}^+)$
,
$h\in C_b^{2,5}(\mathbb{R}^+)$
,
 \begin{align} \big|\mathbb{E} [h(\chi^2)] - \chi^2_{(r-1)} h \big| & \leq \frac{1}{n}\bigg(\!\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}\bigg)^2\big\{19\|h^{\prime\prime}\|+206\|h^{(3)}\|\nonumber\\ & \quad + 545\|h^{(4)}\|+161\,348\|h^{(5)}\|\big\}, \end{align}
\begin{align} \big|\mathbb{E} [h(\chi^2)] - \chi^2_{(r-1)} h \big| & \leq \frac{1}{n}\bigg(\!\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}\bigg)^2\big\{19\|h^{\prime\prime}\|+206\|h^{(3)}\|\nonumber\\ & \quad + 545\|h^{(4)}\|+161\,348\|h^{(5)}\|\big\}, \end{align}
and, for
![]() $h \in C_b^{2,2}(\mathbb{R}^+)$
,
$h \in C_b^{2,2}(\mathbb{R}^+)$
,
 \begin{equation} \big|\mathbb{E} [h(\chi^2)] - \chi^2_{(r-1)} h \big| \leq \frac{238\|h^{\prime\prime}\|}{\sqrt{n}}\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}. \end{equation}
\begin{equation} \big|\mathbb{E} [h(\chi^2)] - \chi^2_{(r-1)} h \big| \leq \frac{238\|h^{\prime\prime}\|}{\sqrt{n}}\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}. \end{equation}
The following weak convergence theorem for smooth test functions with a bound of order
![]() $n^{-1}$
for the
$n^{-1}$
for the
![]() $\chi_{(r-1)}^2$
approximation of the power divergence statistic
$\chi_{(r-1)}^2$
approximation of the power divergence statistic
![]() $T_\lambda$
(which holds for all
$T_\lambda$
(which holds for all
![]() $\lambda>-1$
and
$\lambda>-1$
and
![]() $r\geq2$
) is the main result of this paper.
$r\geq2$
) is the main result of this paper.
Theorem 2. Let
![]() $(U_1, \ldots, U_r)$
represent the multinomial vector of n observed counts, where
$(U_1, \ldots, U_r)$
represent the multinomial vector of n observed counts, where
![]() $r \geq 2$
. For
$r \geq 2$
. For
![]() $\lambda>-1$
, let
$\lambda>-1$
, let
![]() $T_\lambda$
be the power divergence statistic as defined in (1). Suppose that
$T_\lambda$
be the power divergence statistic as defined in (1). Suppose that
![]() $np_*\geq r$
. If
$np_*\geq r$
. If
![]() $\lambda\geq3$
, we also suppose that
$\lambda\geq3$
, we also suppose that
![]() $np_*\geq 2(\lambda-3)^2$
. Then, for
$np_*\geq 2(\lambda-3)^2$
. Then, for
![]() $h \in C_b^5(\mathbb{R}^+)$
,
$h \in C_b^5(\mathbb{R}^+)$
,
 \begin{align} \big|\mathbb{E} [h(T_\lambda)] - \chi^2_{(r-1)} h \big| & \leq \frac{1}{n}\bigg(\!\sum_{j=1}^r\frac{1}{p_j}\bigg)\bigg\{\frac{4r}{r+1}\big\{19\|h\|+366\|h^{\prime}\|+2016\|h^{\prime\prime}\|\nonumber\\ &\quad+5264\|h^{(3)}\|+106\,965\|h^{(4)}\|+302\,922\|h^{(5)}\|\big\}\nonumber\\ &\quad+|\lambda-1|r\big\{2\|h^{\prime}\|+202\|h^{\prime\prime}\|+819\|h^{(3)}\|+100\,974\|h^{(4)}\|\big\}\nonumber\\ &\quad+\frac{19}{9}(\lambda-1)^2\|h^{\prime\prime}\|+\frac{|(\lambda-1)(\lambda-2)|(12\lambda+13)}{6(\lambda+1)}\|h^{\prime}\|\bigg\}. \end{align}
\begin{align} \big|\mathbb{E} [h(T_\lambda)] - \chi^2_{(r-1)} h \big| & \leq \frac{1}{n}\bigg(\!\sum_{j=1}^r\frac{1}{p_j}\bigg)\bigg\{\frac{4r}{r+1}\big\{19\|h\|+366\|h^{\prime}\|+2016\|h^{\prime\prime}\|\nonumber\\ &\quad+5264\|h^{(3)}\|+106\,965\|h^{(4)}\|+302\,922\|h^{(5)}\|\big\}\nonumber\\ &\quad+|\lambda-1|r\big\{2\|h^{\prime}\|+202\|h^{\prime\prime}\|+819\|h^{(3)}\|+100\,974\|h^{(4)}\|\big\}\nonumber\\ &\quad+\frac{19}{9}(\lambda-1)^2\|h^{\prime\prime}\|+\frac{|(\lambda-1)(\lambda-2)|(12\lambda+13)}{6(\lambda+1)}\|h^{\prime}\|\bigg\}. \end{align}
Also, under the weaker assumption that
![]() $h\in C_b^{1,5}(\mathbb{R}^+)$
,
$h\in C_b^{1,5}(\mathbb{R}^+)$
,
 \begin{align} \big|\mathbb{E} [h(T_\lambda)] - \chi^2_{(r-1)} h \big| & \leq \frac{1}{n}\bigg(\!\sum_{j=1}^r\frac{1}{p_j}\bigg)\bigg\{\frac{r}{\sqrt{r+1}\,}\big\{122\|h^{\prime}\|+1970\|h^{\prime\prime}\|\nonumber\\ &\quad+6943\|h^{(3)}\|+12\,731\|h^{(4)}\|+643\,710\|h^{(5)}\|\big\}\nonumber\\ &\quad+|\lambda-1|r\big\{2\|h^{\prime}\|+202\|h^{\prime\prime}\|+819\|h^{(3)}\|+100\,974\|h^{(4)}\|\big\}\nonumber\\ &\quad+\frac{19}{9}(\lambda-1)^2\|h^{\prime\prime}\|+\frac{|(\lambda-1)(\lambda-2)|(12\lambda+13)}{6(\lambda+1)}\|h^{\prime}\|\bigg\}. \end{align}
\begin{align} \big|\mathbb{E} [h(T_\lambda)] - \chi^2_{(r-1)} h \big| & \leq \frac{1}{n}\bigg(\!\sum_{j=1}^r\frac{1}{p_j}\bigg)\bigg\{\frac{r}{\sqrt{r+1}\,}\big\{122\|h^{\prime}\|+1970\|h^{\prime\prime}\|\nonumber\\ &\quad+6943\|h^{(3)}\|+12\,731\|h^{(4)}\|+643\,710\|h^{(5)}\|\big\}\nonumber\\ &\quad+|\lambda-1|r\big\{2\|h^{\prime}\|+202\|h^{\prime\prime}\|+819\|h^{(3)}\|+100\,974\|h^{(4)}\|\big\}\nonumber\\ &\quad+\frac{19}{9}(\lambda-1)^2\|h^{\prime\prime}\|+\frac{|(\lambda-1)(\lambda-2)|(12\lambda+13)}{6(\lambda+1)}\|h^{\prime}\|\bigg\}. \end{align}
If the constants are large compared to n, the next result may give smaller numerical bounds.
Theorem 3. Let
![]() $\lambda>-1$
,
$\lambda>-1$
,
![]() $r\geq2$
, and
$r\geq2$
, and
![]() $np_*\geq 2$
. If
$np_*\geq 2$
. If
![]() $\lambda\geq2$
, we also suppose that
$\lambda\geq2$
, we also suppose that
![]() $np_*\geq 2(\lambda-2)^2$
. Then, for
$np_*\geq 2(\lambda-2)^2$
. Then, for
![]() $h \in C_b^2(\mathbb{R}^+)$
,
$h \in C_b^2(\mathbb{R}^+)$
,
 \begin{align} \big|\mathbb{E} [h(T_\lambda)] - \chi^2_{(r-1)} h \big| \\ \cr&\!\!\!\!\!\!\!\!\leq \bigg(\frac{24}{r+1}\big\{3\|h\|+23\|h^{\prime}\|+42\|h^{\prime\prime}\|\big\}+\frac{|\lambda-1|(4\lambda+7)}{\lambda+1}\|h^{\prime}\|\bigg)\sum_{j=1}^r\frac{1}{\sqrt{np_j}\,}. \end{align}
\begin{align} \big|\mathbb{E} [h(T_\lambda)] - \chi^2_{(r-1)} h \big| \\ \cr&\!\!\!\!\!\!\!\!\leq \bigg(\frac{24}{r+1}\big\{3\|h\|+23\|h^{\prime}\|+42\|h^{\prime\prime}\|\big\}+\frac{|\lambda-1|(4\lambda+7)}{\lambda+1}\|h^{\prime}\|\bigg)\sum_{j=1}^r\frac{1}{\sqrt{np_j}\,}. \end{align}
Also, under the weaker assumption that
![]() $h\in C_b^{1,2}(\mathbb{R}^+)$
,
$h\in C_b^{1,2}(\mathbb{R}^+)$
,
 \begin{align} \big|\mathbb{E} [h(T_\lambda)] - \chi^2_{(r-1)} h \big| \\ \cr&\!\!\!\!\!\!\!\!\leq \bigg(\frac{1}{\sqrt{r+1}\,}\big\{115\|h^{\prime}\|+536\|h^{\prime\prime}\|\big\}+\frac{|\lambda-1|(4\lambda+7)}{\lambda+1}\|h^{\prime}\|\bigg)\sum_{j=1}^r\frac{1}{\sqrt{np_j}\,}. \end{align}
\begin{align} \big|\mathbb{E} [h(T_\lambda)] - \chi^2_{(r-1)} h \big| \\ \cr&\!\!\!\!\!\!\!\!\leq \bigg(\frac{1}{\sqrt{r+1}\,}\big\{115\|h^{\prime}\|+536\|h^{\prime\prime}\|\big\}+\frac{|\lambda-1|(4\lambda+7)}{\lambda+1}\|h^{\prime}\|\bigg)\sum_{j=1}^r\frac{1}{\sqrt{np_j}\,}. \end{align}
In the following corollary we deduce a Kolmogorov distance bound from (12) by applying a basic technique (see [Reference Chen, Goldstein and Shao6, p. 48]) for converting smooth test function bounds into Kolmogorov distance bounds. As this technique is fairly crude, our resulting bound has a suboptimal dependence on n, although it does inherit the desirable property of decaying to zero if and only if
![]() $np_*\rightarrow\infty$
, for fixed r and
$np_*\rightarrow\infty$
, for fixed r and
![]() $\lambda$
. This is the first Kolmogorov distance bound for the chi-square approximation of the statistic
$\lambda$
. This is the first Kolmogorov distance bound for the chi-square approximation of the statistic
![]() $T_\lambda$
to enjoy this property.
$T_\lambda$
to enjoy this property.
Corollary 1. Let
![]() $\lambda>-1$
,
$\lambda>-1$
,
![]() $r\geq2$
. and
$r\geq2$
. and
![]() $np_*\geq 2$
. If
$np_*\geq 2$
. If
![]() $\lambda\geq2$
, we additionally suppose that
$\lambda\geq2$
, we additionally suppose that
![]() $np_*\geq 2(\lambda-2)^2$
. Also, let
$np_*\geq 2(\lambda-2)^2$
. Also, let
![]() $Y_{r-1}\sim\chi_{(r-1)}^2$
. Then
$Y_{r-1}\sim\chi_{(r-1)}^2$
. Then
 \begin{align*} & \sup_{z>0}\big|\mathbb{P}(T_\lambda\leq z)-\mathbb{P}(Y_{r-1}\leq z)\big| \\[9pt]
& \quad \quad \quad \quad \leq \begin{cases} \displaystyle \frac{1}{(np_*)^{1/10}}\bigg\{8+\bigg(21+\frac{|\lambda-1|(4\lambda+7)r}{52(\lambda+1)}\bigg)\frac{1}{(np_*)^{1/5}}+\frac{72}{(np_*)^{2/5}}\bigg\}, \: r=2, \\[9pt]
\displaystyle \frac{1}{(np_*)^{1/6}}\bigg\{19+\bigg(44+\frac{|\lambda-1|(4\lambda+7)r}{25(\lambda+1)}\bigg)\frac{1}{(np_*)^{1/6}}+\frac{72}{(np_*)^{1/3}}\bigg\}, \: r=3, \\[9pt] \displaystyle \frac{1}{(r-3)^{1/3}(np_*)^{1/6}}\bigg\{13+\bigg(37+\frac{|\lambda-1|(4\lambda+7)r}{30(\lambda+1)}\bigg)\frac{(r-3)^{1/6}}{(np_*)^{1/6}}\\[9pt] \displaystyle \qquad\qquad\qquad\qquad\quad + \frac{72(r-3)^{1/3}}{(np_*)^{1/3}}\bigg\}, \: \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, r\geq4. \end{cases} \end{align*}
\begin{align*} & \sup_{z>0}\big|\mathbb{P}(T_\lambda\leq z)-\mathbb{P}(Y_{r-1}\leq z)\big| \\[9pt]
& \quad \quad \quad \quad \leq \begin{cases} \displaystyle \frac{1}{(np_*)^{1/10}}\bigg\{8+\bigg(21+\frac{|\lambda-1|(4\lambda+7)r}{52(\lambda+1)}\bigg)\frac{1}{(np_*)^{1/5}}+\frac{72}{(np_*)^{2/5}}\bigg\}, \: r=2, \\[9pt]
\displaystyle \frac{1}{(np_*)^{1/6}}\bigg\{19+\bigg(44+\frac{|\lambda-1|(4\lambda+7)r}{25(\lambda+1)}\bigg)\frac{1}{(np_*)^{1/6}}+\frac{72}{(np_*)^{1/3}}\bigg\}, \: r=3, \\[9pt] \displaystyle \frac{1}{(r-3)^{1/3}(np_*)^{1/6}}\bigg\{13+\bigg(37+\frac{|\lambda-1|(4\lambda+7)r}{30(\lambda+1)}\bigg)\frac{(r-3)^{1/6}}{(np_*)^{1/6}}\\[9pt] \displaystyle \qquad\qquad\qquad\qquad\quad + \frac{72(r-3)^{1/3}}{(np_*)^{1/3}}\bigg\}, \: \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, r\geq4. \end{cases} \end{align*}
Remark 1. (On the proofs and assumptions.) Our proofs of Theorems 2 and 3 involve writing the power divergence statistic
![]() $T_\lambda$
in the form
$T_\lambda$
in the form
![]() $T_\lambda=\chi^2+R$
, where R is a ‘small’ remainder term. By this approach, to obtain our bounds on the quantity of interest
$T_\lambda=\chi^2+R$
, where R is a ‘small’ remainder term. By this approach, to obtain our bounds on the quantity of interest
![]() $\big|\mathbb{E}[h(T_\lambda)]-\chi_{(r-1)}^2h\big|$
, we make use of the bounds on
$\big|\mathbb{E}[h(T_\lambda)]-\chi_{(r-1)}^2h\big|$
, we make use of the bounds on
![]() $\big|\mathbb{E}[h(\chi^2)]-\chi_{(r-1)}^2h\big|$
given by (4)–(7). In the case
$\big|\mathbb{E}[h(\chi^2)]-\chi_{(r-1)}^2h\big|$
given by (4)–(7). In the case
![]() $\lambda=1$
,
$\lambda=1$
,
![]() $T_\lambda=\chi^2$
, meaning that
$T_\lambda=\chi^2$
, meaning that
![]() $R=0$
, which explains why our bounds reduce almost exactly to those bounds when
$R=0$
, which explains why our bounds reduce almost exactly to those bounds when
![]() $\lambda=1$
, with the only difference being that at the end of our proof of Theorem 2 we use the inequality
$\lambda=1$
, with the only difference being that at the end of our proof of Theorem 2 we use the inequality
![]() $\big(\!\sum_{j=1}^rp_j^{-1/2}\big)^2\leq r\sum_{j=1}^rp_j^{-1}$
to obtain a compact final bound.
$\big(\!\sum_{j=1}^rp_j^{-1/2}\big)^2\leq r\sum_{j=1}^rp_j^{-1}$
to obtain a compact final bound.
Our approach of decomposing
![]() $T_\lambda=\chi^2+R$
means that we inherit large numerical constants from the bounds (4)–(7). However, as was the case in [Reference Gaunt, Pickett and Reinert14], our primary concern is simple final bounds with good dependence on the parameters n,
$T_\lambda=\chi^2+R$
means that we inherit large numerical constants from the bounds (4)–(7). However, as was the case in [Reference Gaunt, Pickett and Reinert14], our primary concern is simple final bounds with good dependence on the parameters n,
![]() $\lambda$
, r, and
$\lambda$
, r, and
![]() $p_1,\ldots,p_r$
. In proving Theorems 2 and 3, we make some crude approximations but take care to ensure they do not affect the role of the parameters in the final bound.
$p_1,\ldots,p_r$
. In proving Theorems 2 and 3, we make some crude approximations but take care to ensure they do not affect the role of the parameters in the final bound.
In order to simplify the calculations and arrive at our desired compact final bounds, we made some assumptions. We discuss here the assumptions for Theorem 2; similar comments apply to the assumptions of Theorem 3. The assumption
![]() $np_*\geq r$
(
$np_*\geq r$
(
![]() $\lambda\not=1$
),
$\lambda\not=1$
),
![]() $np_*\geq1$
(
$np_*\geq1$
(
![]() $\lambda=1$
) is very mild (the bounds in Theorem 2 are uninformative otherwise) and was made for the purpose of simplifying the calculations and to allow us to obtain a compact final bound (it allows the bound of Lemma 3 to be given in a compact form). This assumption is also natural, because we require that
$\lambda=1$
) is very mild (the bounds in Theorem 2 are uninformative otherwise) and was made for the purpose of simplifying the calculations and to allow us to obtain a compact final bound (it allows the bound of Lemma 3 to be given in a compact form). This assumption is also natural, because we require that
![]() $np_*/r\rightarrow\infty$
in order for
$np_*/r\rightarrow\infty$
in order for
![]() $T_{\lambda}\rightarrow_\mathrm{d} \chi_{(r-1)}^2$
(see Remark 3). The assumption
$T_{\lambda}\rightarrow_\mathrm{d} \chi_{(r-1)}^2$
(see Remark 3). The assumption
![]() $np_*\geq 2(\lambda-3)^2$
,
$np_*\geq 2(\lambda-3)^2$
,
![]() $\lambda\geq3$
, is also mild (our bound cannot be small unless this condition is met) and natural because a necessary condition for
$\lambda\geq3$
, is also mild (our bound cannot be small unless this condition is met) and natural because a necessary condition for
![]() $T_{\lambda}\rightarrow_\mathrm{d} \chi_{(r-1)}^2$
is that
$T_{\lambda}\rightarrow_\mathrm{d} \chi_{(r-1)}^2$
is that
![]() $np_*/\lambda^2\rightarrow\infty$
(see Remark 3). This assumption is needed to apply Lemma 2 and, again, is useful in allowing a compact bound to be given.
$np_*/\lambda^2\rightarrow\infty$
(see Remark 3). This assumption is needed to apply Lemma 2 and, again, is useful in allowing a compact bound to be given.
Remark 2. (The class of functions and integral probability metrics (IPMs).) The bound (10) of Theorem 2 is in a sense preferable to the bound (11) because in the case
![]() $\lambda=1$
it has a better dependence on r. However, an advantage of the bound (11) is that it holds for a wider class of test functions h while having the same dependence on all parameters n,
$\lambda=1$
it has a better dependence on r. However, an advantage of the bound (11) is that it holds for a wider class of test functions h while having the same dependence on all parameters n,
![]() $\lambda$
, r, and
$\lambda$
, r, and
![]() $p_1,\ldots,p_r$
if
$p_1,\ldots,p_r$
if
![]() $\lambda\not=1$
. We now see how this advantage plays out if the smooth test function bounds are converted into bounds involving integral probability metrics.
$\lambda\not=1$
. We now see how this advantage plays out if the smooth test function bounds are converted into bounds involving integral probability metrics.
The bounds of Theorems 1–3 can be expressed in terms of convergence determining IPMs [Reference Gibbs and Su16, Reference Zolotarev39] as follows. Let
![]() $\mathcal{H}_{q_1,q_2}=\{h\in C_b^{q_1,q_2}(\mathbb{R}^+) \,:\, \|h^{(q_1)}\|\leq1,\|h^{(q_1+1)}\|\leq1,\ldots,\|h^{(q_2-1)}\|\leq1,\|h^{(q_2)}\|\leq1\}$
, where
$\mathcal{H}_{q_1,q_2}=\{h\in C_b^{q_1,q_2}(\mathbb{R}^+) \,:\, \|h^{(q_1)}\|\leq1,\|h^{(q_1+1)}\|\leq1,\ldots,\|h^{(q_2-1)}\|\leq1,\|h^{(q_2)}\|\leq1\}$
, where
![]() $h^{(0)}\equiv h$
. Then we define the IPM between the laws of real-valued random variables X and Y by
$h^{(0)}\equiv h$
. Then we define the IPM between the laws of real-valued random variables X and Y by
![]() $d_{q_1,q_2}(\mathcal{L}(X),\mathcal{L}(Y))=\sup_{h\in\mathcal{H}_{q_1,q_2}}\big|\mathbb{E}[h(X)]-\mathbb{E}[h(Y)]\big|$
. As an example, for
$d_{q_1,q_2}(\mathcal{L}(X),\mathcal{L}(Y))=\sup_{h\in\mathcal{H}_{q_1,q_2}}\big|\mathbb{E}[h(X)]-\mathbb{E}[h(Y)]\big|$
. As an example, for
![]() $Y_{r-1}\sim\chi_{(r-1)}^2$
, from (11) we obtain the two-sided inequality
$Y_{r-1}\sim\chi_{(r-1)}^2$
, from (11) we obtain the two-sided inequality
 \begin{multline} \big|\mathbb{E}[T_\lambda]-\mathbb{E}[Y_{r-1}]\big| \leq d_{1,5}\big(\mathcal{L}(T_\lambda),\chi_{(r-1)}^2\big)\leq \frac{1}{n}\bigg(\!\sum_{j=1}^r\frac{1}{p_j}\bigg)\bigg\{665\,476\sqrt{r} \\+101\,997|\lambda-1|r+\frac{19}{9}(\lambda-1)^2+\frac{|(\lambda-1)(\lambda-2)|(12\lambda+13)}{6(\lambda+1)}\bigg\}, \end{multline}
\begin{multline} \big|\mathbb{E}[T_\lambda]-\mathbb{E}[Y_{r-1}]\big| \leq d_{1,5}\big(\mathcal{L}(T_\lambda),\chi_{(r-1)}^2\big)\leq \frac{1}{n}\bigg(\!\sum_{j=1}^r\frac{1}{p_j}\bigg)\bigg\{665\,476\sqrt{r} \\+101\,997|\lambda-1|r+\frac{19}{9}(\lambda-1)^2+\frac{|(\lambda-1)(\lambda-2)|(12\lambda+13)}{6(\lambda+1)}\bigg\}, \end{multline}
where the lower bound follows because
![]() $h(x)=x$
is in the class
$h(x)=x$
is in the class
![]() $\mathcal{H}_{1,5}$
. If
$\mathcal{H}_{1,5}$
. If
![]() $r\geq2$
, then
$r\geq2$
, then
![]() $\mathbb{E}[T_1]=\mathbb{E}[\chi^2]=\mathbb{E}[Y_{r-1}]$
, and it was shown in [Reference Cressie and Read7, p. 451] (here we have written their formula in a slightly different form) that, for
$\mathbb{E}[T_1]=\mathbb{E}[\chi^2]=\mathbb{E}[Y_{r-1}]$
, and it was shown in [Reference Cressie and Read7, p. 451] (here we have written their formula in a slightly different form) that, for
![]() $\lambda>-1$
,
$\lambda>-1$
,
 \begin{align} \big|\mathbb{E}[T_\lambda]-\mathbb{E}[Y_{r-1}]\big| = \bigg|\sum_{j=1}^r\bigg\{\frac{(\lambda-1)}{np_j}\bigg[\frac{3\lambda-2}{12}-\frac{\lambda p_j}{2}+\frac{3\lambda+2}{12}p_j^2\bigg]\bigg\}+O(n^{-3/2})\bigg|.\end{align}
\begin{align} \big|\mathbb{E}[T_\lambda]-\mathbb{E}[Y_{r-1}]\big| = \bigg|\sum_{j=1}^r\bigg\{\frac{(\lambda-1)}{np_j}\bigg[\frac{3\lambda-2}{12}-\frac{\lambda p_j}{2}+\frac{3\lambda+2}{12}p_j^2\bigg]\bigg\}+O(n^{-3/2})\bigg|.\end{align}
It should be noted that
![]() $\mathbb{E}[T_{-1}]=\infty$
, and that the
$\mathbb{E}[T_{-1}]=\infty$
, and that the
![]() $O(n^{-3/2})$
term in the asymptotic approximation for
$O(n^{-3/2})$
term in the asymptotic approximation for
![]() $\big|\mathbb{E}[T_\lambda]-\mathbb{E}[Y_{r-1}]\big|$
therefore blows up as
$\big|\mathbb{E}[T_\lambda]-\mathbb{E}[Y_{r-1}]\big|$
therefore blows up as
![]() $\lambda\downarrow-1$
. We also note that comparing the lower and upper bounds in (14) shows that the upper bound (14) has a good dependence on all parameters, n,
$\lambda\downarrow-1$
. We also note that comparing the lower and upper bounds in (14) shows that the upper bound (14) has a good dependence on all parameters, n,
![]() $\lambda$
, r, and
$\lambda$
, r, and
![]() $p_1,\ldots,p_r$
. This is the subject of the next remark.
$p_1,\ldots,p_r$
. This is the subject of the next remark.
Remark 3. (The dependence of the bounds on the parameters and conditions for convergence.) A basic necessary condition for
![]() $T_\lambda$
to converge in distribution to
$T_\lambda$
to converge in distribution to
![]() $\chi_{(r-1)}^2$
is that
$\chi_{(r-1)}^2$
is that
![]() $\mathbb{E}[T_\lambda]\rightarrow\mathbb{E}[Y_{r-1}]$
for
$\mathbb{E}[T_\lambda]\rightarrow\mathbb{E}[Y_{r-1}]$
for
![]() $Y_{r-1}\sim\chi_{(r-1)}^2$
. Therefore, we can study the optimality of the bounds of Theorems 2 and 3 on the parameters n,
$Y_{r-1}\sim\chi_{(r-1)}^2$
. Therefore, we can study the optimality of the bounds of Theorems 2 and 3 on the parameters n,
![]() $\lambda$
, r, and
$\lambda$
, r, and
![]() $p_1,\ldots,p_r$
via comparison with the asymptotic approximation in (15). We observe that the
$p_1,\ldots,p_r$
via comparison with the asymptotic approximation in (15). We observe that the
![]() $O(n^{-1})$
rate of convergence of the upper bounds in Theorem 2 is optimal. Moreover, the dependence on
$O(n^{-1})$
rate of convergence of the upper bounds in Theorem 2 is optimal. Moreover, the dependence on
![]() $p_*$
of the form
$p_*$
of the form
![]() $(np_*)^{-1}$
is also the best possible, as is the dependence on
$(np_*)^{-1}$
is also the best possible, as is the dependence on
![]() $\lambda$
of the form
$\lambda$
of the form
![]() $\lambda^2/n$
for large n and
$\lambda^2/n$
for large n and
![]() $\lambda$
. The bounds in Theorem 3 are of the suboptimal order
$\lambda$
. The bounds in Theorem 3 are of the suboptimal order
![]() $O(n^{-1/2})$
, but otherwise also have the correct dependence on
$O(n^{-1/2})$
, but otherwise also have the correct dependence on
![]() $p_*$
and
$p_*$
and
![]() $\lambda$
, because they tend to zero if and only if
$\lambda$
, because they tend to zero if and only if
![]() $np_*\rightarrow\infty$
(with fixed r and
$np_*\rightarrow\infty$
(with fixed r and
![]() $\lambda$
) and
$\lambda$
) and
![]() $n/\lambda^2\rightarrow\infty$
(with fixed r and
$n/\lambda^2\rightarrow\infty$
(with fixed r and
![]() $p_*$
).
$p_*$
).
Let us now consider the dependence of the bounds of Theorems 2 and 3 on r. To do this, we consider the case of uniform cell classification probabilities,
![]() $p_1=\cdots=p_r=1/r$
, and suppose
$p_1=\cdots=p_r=1/r$
, and suppose
![]() $\lambda\not=1$
is fixed. Then, for large r,
$\lambda\not=1$
is fixed. Then, for large r,
![]() $\big|\mathbb{E}[T_\lambda]-\mathbb{E}[Y_{r-1}]\big|\rightarrow0$
if and only if
$\big|\mathbb{E}[T_\lambda]-\mathbb{E}[Y_{r-1}]\big|\rightarrow0$
if and only if
![]() $n/r^2\rightarrow\infty$
, except when
$n/r^2\rightarrow\infty$
, except when
![]() $\lambda=2/3$
, in which case
$\lambda=2/3$
, in which case
![]() $\big|\mathbb{E}[T_{2/3}]-\mathbb{E}[Y_{r-1}]\big|\rightarrow0$
if and only if
$\big|\mathbb{E}[T_{2/3}]-\mathbb{E}[Y_{r-1}]\big|\rightarrow0$
if and only if
![]() $n/r\rightarrow\infty$
. In this case of uniform cell classification probabilities, the bounds of Theorems 2 and 3 converge to zero, for fixed
$n/r\rightarrow\infty$
. In this case of uniform cell classification probabilities, the bounds of Theorems 2 and 3 converge to zero, for fixed
![]() $\lambda\not=1$
, if and only if
$\lambda\not=1$
, if and only if
![]() $n/r^3\rightarrow\infty$
. We consider it most likely that
$n/r^3\rightarrow\infty$
. We consider it most likely that
![]() $T_\lambda\rightarrow_\mathrm{d}\chi_{(r-1)}^2$
if
$T_\lambda\rightarrow_\mathrm{d}\chi_{(r-1)}^2$
if
![]() $n/r^2\rightarrow\infty$
, and that our bounds therefore do not have an optimal dependence on r. In the proof of Theorem 2, our bounds for all the remainder terms except
$n/r^2\rightarrow\infty$
, and that our bounds therefore do not have an optimal dependence on r. In the proof of Theorem 2, our bounds for all the remainder terms except
![]() $R_3$
decay to zero if and only if
$R_3$
decay to zero if and only if
![]() $n/r^2\rightarrow\infty$
, while our bound for
$n/r^2\rightarrow\infty$
, while our bound for
![]() $R_3$
decays to zero if and only if
$R_3$
decays to zero if and only if
![]() $n/r^3\rightarrow\infty$
. The bound for
$n/r^3\rightarrow\infty$
. The bound for
![]() $R_3$
follows from a long calculation involving analysis of the multivariate normal Stein equation; see Part II of the proof of [Reference Gaunt, Pickett and Reinert14, Theorem 4.2]. It is plausible that a more refined analysis could lead to a bound for
$R_3$
follows from a long calculation involving analysis of the multivariate normal Stein equation; see Part II of the proof of [Reference Gaunt, Pickett and Reinert14, Theorem 4.2]. It is plausible that a more refined analysis could lead to a bound for
![]() $R_3$
with an improved dependence on r. We consider this to be an interesting but challenging problem.
$R_3$
with an improved dependence on r. We consider this to be an interesting but challenging problem.
If we consider the possibility that, as
![]() $n\rightarrow\infty$
,
$n\rightarrow\infty$
,
![]() $p_*$
may decay to zero,
$p_*$
may decay to zero,
![]() $\lambda\not=1$
, and r may tend to infinity, we can read off from the upper bounds of Theorem 2 that
$\lambda\not=1$
, and r may tend to infinity, we can read off from the upper bounds of Theorem 2 that
![]() $T_\lambda\rightarrow_\mathrm{d}\chi_{(r-1)}^2$
if
$T_\lambda\rightarrow_\mathrm{d}\chi_{(r-1)}^2$
if
![]() $n/(S\lambda\max\{r,\lambda\})\rightarrow\infty$
, where
$n/(S\lambda\max\{r,\lambda\})\rightarrow\infty$
, where
![]() $S=\sum_{j=1}^rp_j^{-1}$
. If we suppose that
$S=\sum_{j=1}^rp_j^{-1}$
. If we suppose that
![]() $r/\lambda\rightarrow c$
, where
$r/\lambda\rightarrow c$
, where
![]() $0\leq c<\infty$
, then we see that
$0\leq c<\infty$
, then we see that
![]() $T_\lambda\rightarrow_\mathrm{d}\chi_{(r-1)}^2$
if
$T_\lambda\rightarrow_\mathrm{d}\chi_{(r-1)}^2$
if
![]() $n/(S\lambda^2)\rightarrow\infty$
. From (15) this can be seen to be an optimal condition (except perhaps if
$n/(S\lambda^2)\rightarrow\infty$
. From (15) this can be seen to be an optimal condition (except perhaps if
![]() $\lambda=2/3$
). We conjecture that in fact
$\lambda=2/3$
). We conjecture that in fact
![]() $T_\lambda\rightarrow_\mathrm{d}\chi_{(r-1)}^2$
if
$T_\lambda\rightarrow_\mathrm{d}\chi_{(r-1)}^2$
if
![]() $n/(S\lambda^2)\rightarrow\infty$
, even if
$n/(S\lambda^2)\rightarrow\infty$
, even if
![]() $r\gg\lambda$
(except perhaps if
$r\gg\lambda$
(except perhaps if
![]() $\lambda=2/3$
).
$\lambda=2/3$
).
In stating the above conditions we have been careful to give them in terms of the sum S rather than
![]() $p_*$
, because in the
$p_*$
, because in the
![]() $r\rightarrow\infty$
regime it is possible that
$r\rightarrow\infty$
regime it is possible that
![]() $S\ll r/p_*$
. For example, take
$S\ll r/p_*$
. For example, take
![]() $p_1=n^{-1}$
,
$p_1=n^{-1}$
,
![]() $p_j=(n-1)/(n(r-1))$
,
$p_j=(n-1)/(n(r-1))$
,
![]() $j=2,\ldots,r$
, so that
$j=2,\ldots,r$
, so that
![]() $\sum_{j=1}^rp_j=1$
. Then
$\sum_{j=1}^rp_j=1$
. Then
![]() $S=n+(r-1)^2n/(n-1)\ll rn=r/p_*$
if
$S=n+(r-1)^2n/(n-1)\ll rn=r/p_*$
if
![]() $r\ll n$
. If, however,
$r\ll n$
. If, however,
![]() $r/(p_*S)\rightarrow C$
, where
$r/(p_*S)\rightarrow C$
, where
![]() $1\leq C<\infty$
(which will be the case unless there are some exceptionally small cell classification probabilities), then we can write the conditions in a simple and intuitive form by replacing S by
$1\leq C<\infty$
(which will be the case unless there are some exceptionally small cell classification probabilities), then we can write the conditions in a simple and intuitive form by replacing S by
![]() $r/p_*$
. For example, our conjectured optimal condition for which
$r/p_*$
. For example, our conjectured optimal condition for which
![]() $T_\lambda\rightarrow_\mathrm{d}\chi_{(r-1)}^2$
would read
$T_\lambda\rightarrow_\mathrm{d}\chi_{(r-1)}^2$
would read
![]() $np_*/(r\lambda^2)\rightarrow\infty$
.
$np_*/(r\lambda^2)\rightarrow\infty$
.
From (5) we see that, even if
![]() $r\rightarrow\infty$
,
$r\rightarrow\infty$
,
![]() $T_1=\chi^2\rightarrow_\mathrm{d}\chi_{(r-1)}^2$
provided
$T_1=\chi^2\rightarrow_\mathrm{d}\chi_{(r-1)}^2$
provided
![]() $np_*\rightarrow\infty$
, which is a well-established condition for chi-square approximation of Pearson’s statistic to be valid (see [Reference Greenwood and Nikulin18]). Thus, in the
$np_*\rightarrow\infty$
, which is a well-established condition for chi-square approximation of Pearson’s statistic to be valid (see [Reference Greenwood and Nikulin18]). Thus, in the
![]() $r\rightarrow\infty$
regime, it can be seen that Pearson’s statistic converges in distribution faster than any other member of the power divergence family, except perhaps
$r\rightarrow\infty$
regime, it can be seen that Pearson’s statistic converges in distribution faster than any other member of the power divergence family, except perhaps
![]() $T_{2/3}$
for which we are unable to provide a definitive answer in this paper.
$T_{2/3}$
for which we are unable to provide a definitive answer in this paper.
Remark 4. (Comparison to results from simulation studies.) Simulation studies assessing the quality of chi-square approximation of the statistic
![]() $T_\lambda$
can be found in, amongst others, [Reference Cressie and Read7, Reference Medak23, Reference Read30, Reference Read and Cressie32, Reference Rudas33]. In this remark we show how some of the findings of these studies are reflected in our bounds. As is common with small-sample studies for goodness-of-fit tests, most of the studies assumed that the classification probabilities are uniform (
$T_\lambda$
can be found in, amongst others, [Reference Cressie and Read7, Reference Medak23, Reference Read30, Reference Read and Cressie32, Reference Rudas33]. In this remark we show how some of the findings of these studies are reflected in our bounds. As is common with small-sample studies for goodness-of-fit tests, most of the studies assumed that the classification probabilities are uniform (
![]() $p_j=1/r$
for all
$p_j=1/r$
for all
![]() $j=1,\ldots,r$
) [Reference Koehler and Larntz19, p. 339]. Under this assumption, [Reference Read30] concluded that, for
$j=1,\ldots,r$
) [Reference Koehler and Larntz19, p. 339]. Under this assumption, [Reference Read30] concluded that, for
![]() $\lambda\in[1/3,3/2]$
, the chi-square approximation of
$\lambda\in[1/3,3/2]$
, the chi-square approximation of
![]() $T_\lambda$
is accurate for the purpose of hypothesis testing at significance levels between 0.1 and 0.01, provided
$T_\lambda$
is accurate for the purpose of hypothesis testing at significance levels between 0.1 and 0.01, provided
![]() $r\leq6$
and
$r\leq6$
and
![]() $n\geq10$
[that the approximation can be accurate for sample sizes as small as
$n\geq10$
[that the approximation can be accurate for sample sizes as small as
![]() $n=10$
is consistent with the fast
$n=10$
is consistent with the fast
![]() $O(n^{-1})$
rate of convergence of the bounds of Theorem 2]. However, if
$O(n^{-1})$
rate of convergence of the bounds of Theorem 2]. However, if
![]() $|\lambda|$
increases, the approximation becomes worse, and this is magnified as r increases for fixed n [our bounds grow as
$|\lambda|$
increases, the approximation becomes worse, and this is magnified as r increases for fixed n [our bounds grow as
![]() $\lambda$
and r increase]. Outside the equiprobable hypothesis, it is harder to prescribe general rules [Reference Koehler and Larntz19, p. 341], although the accuracy of the approximation diminishes [Reference Perkins, Tygert and Ward26] [as we move away from the equiprobable hypothesis the sum
$\lambda$
and r increase]. Outside the equiprobable hypothesis, it is harder to prescribe general rules [Reference Koehler and Larntz19, p. 341], although the accuracy of the approximation diminishes [Reference Perkins, Tygert and Ward26] [as we move away from the equiprobable hypothesis the sum
![]() $\sum_{j=1}^rp_j^{-1}$
increases].
$\sum_{j=1}^rp_j^{-1}$
increases].
Through a combination of simulation studies and theoretical considerations, [Reference Cressie and Read7] proposed the statistic
![]() $T_{2/3}$
as an alternative to the classical likelihood ratio and Pearson statistics. One of the reasons was because they observed that for the quantities
$T_{2/3}$
as an alternative to the classical likelihood ratio and Pearson statistics. One of the reasons was because they observed that for the quantities
![]() $\mathbb{E}[T_{\lambda}^k]-\mathbb{E}[Y_{r-1}^k]$
,
$\mathbb{E}[T_{\lambda}^k]-\mathbb{E}[Y_{r-1}^k]$
,
![]() $k=1,2,3$
, for
$k=1,2,3$
, for
![]() $Y_{r-1}\sim \chi_{(r-1)}^2$
, the second-order correction terms vanish in the limit
$Y_{r-1}\sim \chi_{(r-1)}^2$
, the second-order correction terms vanish in the limit
![]() $r\rightarrow\infty$
if and only if
$r\rightarrow\infty$
if and only if
![]() $\lambda=2/3,1$
. Our bounds do converge faster in the case
$\lambda=2/3,1$
. Our bounds do converge faster in the case
![]() $r\rightarrow\infty$
if
$r\rightarrow\infty$
if
![]() $\lambda=1$
, but not if
$\lambda=1$
, but not if
![]() $\lambda=2/3$
, and we know that for
$\lambda=2/3$
, and we know that for
![]() $\lambda\in({-}1,\infty)\setminus\{2/3,1\}$
the true convergence rate is indeed slower in this regime. It would be interesting to provide a definitive answer as to whether the convergence rate does speed up in the large-r regime if
$\lambda\in({-}1,\infty)\setminus\{2/3,1\}$
the true convergence rate is indeed slower in this regime. It would be interesting to provide a definitive answer as to whether the convergence rate does speed up in the large-r regime if
![]() $\lambda=2/3$
. We do, however, note that in our method of proof there seems to be nothing special about the case
$\lambda=2/3$
. We do, however, note that in our method of proof there seems to be nothing special about the case
![]() $\lambda=2/3$
, so a different approach would be required to provide a positive answer.
$\lambda=2/3$
, so a different approach would be required to provide a positive answer.
3. Preliminary lemmas
We begin by presenting a series of moment bounds for binomial random variables.
Lemma 1. Let
![]() $S=(U-np)/\sqrt{np}$
, where
$S=(U-np)/\sqrt{np}$
, where
![]() $U\sim \mathrm{Bin}(n,p)$
, for
$U\sim \mathrm{Bin}(n,p)$
, for
![]() $n\geq1$
,
$n\geq1$
,
![]() $0<p<1$
such that
$0<p<1$
such that
![]() $np\geq2$
. Then
$np\geq2$
. Then
Proof. Using standard formulas for the fourth and sixth central moments of the binomial distribution (see, for example [Reference Stuart and Ord36]), we have that
and
 \begin{align*} \mathbb{E}[S^6]&=\frac{1}{(np)^3}\cdot np(1-p)\big[5(3n^2-26n+24)p^4-10(3n^2-26n+24)p^3\\ &\quad+5(3n^2-31n+30)p^2+5(5n-6)p+1\big]\leq 15+\frac{25}{np}+\frac{1}{(np)^2}<28, \end{align*}
\begin{align*} \mathbb{E}[S^6]&=\frac{1}{(np)^3}\cdot np(1-p)\big[5(3n^2-26n+24)p^4-10(3n^2-26n+24)p^3\\ &\quad+5(3n^2-31n+30)p^2+5(5n-6)p+1\big]\leq 15+\frac{25}{np}+\frac{1}{(np)^2}<28, \end{align*}
where we used that
![]() $n\geq1$
,
$n\geq1$
,
![]() $0<p<1$
, and
$0<p<1$
, and
![]() $np\geq2$
to simplify the bounds. Inequality (16) follows from (17) by Hölder’s inequality:
$np\geq2$
to simplify the bounds. Inequality (16) follows from (17) by Hölder’s inequality:
![]() $\mathbb{E}[|S|^3]\leq(\mathbb{E}[S^4])^{3/4}\leq 4^{3/4}<3$
.
$\mathbb{E}[|S|^3]\leq(\mathbb{E}[S^4])^{3/4}\leq 4^{3/4}<3$
.
Lemma 2. (T. D. Ahle [Reference Ahle1].) Let
![]() $U\sim \mathrm{Bin}(n,p)$
, where
$U\sim \mathrm{Bin}(n,p)$
, where
![]() $n\geq1$
and
$n\geq1$
and
![]() $0<p<1$
. Let
$0<p<1$
. Let
![]() $k>0$
. Then
$k>0$
. Then
![]() $\mathbb{E}[U^k] \leq \exp\!(k^2/(2np))\cdot(np)^k$
. Suppose now that
$\mathbb{E}[U^k] \leq \exp\!(k^2/(2np))\cdot(np)^k$
. Suppose now that
![]() $np\geq \alpha k^2$
, where
$np\geq \alpha k^2$
, where
![]() $\alpha>0$
. Then it is immediate from the previous expression that
$\alpha>0$
. Then it is immediate from the previous expression that
Remark 5. Bounds of the form
![]() $\mathbb{E}[U^k]\leq C_k(np)^k$
, where
$\mathbb{E}[U^k]\leq C_k(np)^k$
, where
![]() $C_k$
is an explicit constant only depending on k, in which there are no further restrictions on n and p, are available (see [Reference Pinelis28]). However, for our purpose of obtaining bounds with the best possible dependence on all parameters, such a bound is not suitable, as it would lead to a worse dependence on
$C_k$
is an explicit constant only depending on k, in which there are no further restrictions on n and p, are available (see [Reference Pinelis28]). However, for our purpose of obtaining bounds with the best possible dependence on all parameters, such a bound is not suitable, as it would lead to a worse dependence on
![]() $\lambda$
in the final bound. The additional assumption
$\lambda$
in the final bound. The additional assumption
![]() $np\geq \alpha k^2$
for inequality (19) leads to the assumption
$np\geq \alpha k^2$
for inequality (19) leads to the assumption
![]() $np\geq 2(\lambda-3)^2$
,
$np\geq 2(\lambda-3)^2$
,
![]() $\lambda\geq3$
, in Theorem 2 (and a similar assumption in Theorem 3), which is mild and preferable to a worse dependence of the bounds on
$\lambda\geq3$
, in Theorem 2 (and a similar assumption in Theorem 3), which is mild and preferable to a worse dependence of the bounds on
![]() $\lambda$
.
$\lambda$
.
Lemma 3. Let
![]() $(U_1,\ldots,U_r$
) be the multinomial vector of observed counts, as in Theorem 2, where
$(U_1,\ldots,U_r$
) be the multinomial vector of observed counts, as in Theorem 2, where
![]() $r\geq2$
. Suppose also that
$r\geq2$
. Suppose also that
![]() $np_j\geq r$
for all
$np_j\geq r$
for all
![]() $j=1,\ldots,r$
. For
$j=1,\ldots,r$
. For
![]() $j=1,\ldots,r$
, let
$j=1,\ldots,r$
, let
![]() $S_j=(U_j-np_j)/\sqrt{np_j}$
. Then, for
$S_j=(U_j-np_j)/\sqrt{np_j}$
. Then, for
![]() $j\not= k$
,
$j\not= k$
,
Proof. Let
![]() $I_j(i)$
be the indicator that trial i results in classification in cell j, and let
$I_j(i)$
be the indicator that trial i results in classification in cell j, and let
![]() $\tilde{I_j}(i) = I_j(i) - p_j$
be its standardised version. We can then write
$\tilde{I_j}(i) = I_j(i) - p_j$
be its standardised version. We can then write
![]() $S_j = (np_j)^{-1/2}\sum_{i=1}^n \tilde{I}_j(i)$
. We note that
$S_j = (np_j)^{-1/2}\sum_{i=1}^n \tilde{I}_j(i)$
. We note that
![]() $\tilde{I_{j_1}}(i_1)$
and
$\tilde{I_{j_1}}(i_1)$
and
![]() $\tilde{I_{j_2}}(i_2)$
are independent for all
$\tilde{I_{j_2}}(i_2)$
are independent for all
![]() $j_1,j_2\in\{1,\ldots,r\}$
if
$j_1,j_2\in\{1,\ldots,r\}$
if
![]() $i_1\not=i_2$
. On using this property together with the fact that
$i_1\not=i_2$
. On using this property together with the fact that
![]() $\mathbb{E}[\tilde{I}_{j}(i)]=0$
for all
$\mathbb{E}[\tilde{I}_{j}(i)]=0$
for all
![]() $i=1,\ldots,n$
and
$i=1,\ldots,n$
and
![]() $j=1,\ldots,r $
, we obtain that, for
$j=1,\ldots,r $
, we obtain that, for
![]() $j\not= k$
,
$j\not= k$
,
 \begin{align} \mathbb{E}[S_j^3S_k^3]&=\frac{1}{n^3(p_jp_k)^{3/2}}\mathbb{E}\Bigg[\Bigg(\!\sum_{i=1}^n \tilde{I}_j(i)\Bigg)^3\Bigg(\!\sum_{\ell=1}^n\tilde{I}_k(\ell)\Bigg)^3\Bigg]\nonumber\\&=\frac{1}{n^3(p_jp_k)^{3/2}}\Bigg\{\sum_{i_1=1}^n\mathbb{E}[\tilde{I}_j(i_1)^3\tilde{I}_k(i_1)^3]+\sum_{i_1=1}^n\sum_{i_2\not=i_1}^n\Big\{\mathbb{E}[\tilde{I}_j(i_1)^3]\mathbb{E}[\tilde{I}_k(i_2)^3]\nonumber\\&\quad+9\mathbb{E}[\tilde{I}_j(i_1)^2\tilde{I}_k(i_1)^2]\mathbb{E}[\tilde{I}_{j}(i_2)\tilde{I}_{k}(i_2)]+3\mathbb{E}[\tilde{I}_j(i_1)^3\tilde{I}_k(i_1)]\mathbb{E}[\tilde{I}_{k}(i_2)^2]\Big\}\nonumber\\&\quad+3\mathbb{E}[\tilde{I}_k(i_1)^3\tilde{I}_j(i_1)]\mathbb{E}[\tilde{I}_{j}(i_2)^2]\nonumber\\&\quad+\sum_{i_1=1}^n\sum_{i_2\not=i_1}^n\sum_{i_3\not=i_1,i_2}^n\Big\{9\mathbb{E}[\tilde{I}_j(i_1)^2]\mathbb{E}[\tilde{I}_j(i_2)\tilde{I}_{k}(i_2)]\mathbb{E}[\tilde{I}_{k}(i_3)^2]\nonumber\\&\quad+6\mathbb{E}[\tilde{I}_j(i_1)\tilde{I}_k(i_1)]\mathbb{E}[\tilde{I}_j(i_2)\tilde{I}_k(i_2)]\mathbb{E}[\tilde{I}_j(i_3)\tilde{I}_k(i_3)]\Big\}\Bigg\}.\end{align}
\begin{align} \mathbb{E}[S_j^3S_k^3]&=\frac{1}{n^3(p_jp_k)^{3/2}}\mathbb{E}\Bigg[\Bigg(\!\sum_{i=1}^n \tilde{I}_j(i)\Bigg)^3\Bigg(\!\sum_{\ell=1}^n\tilde{I}_k(\ell)\Bigg)^3\Bigg]\nonumber\\&=\frac{1}{n^3(p_jp_k)^{3/2}}\Bigg\{\sum_{i_1=1}^n\mathbb{E}[\tilde{I}_j(i_1)^3\tilde{I}_k(i_1)^3]+\sum_{i_1=1}^n\sum_{i_2\not=i_1}^n\Big\{\mathbb{E}[\tilde{I}_j(i_1)^3]\mathbb{E}[\tilde{I}_k(i_2)^3]\nonumber\\&\quad+9\mathbb{E}[\tilde{I}_j(i_1)^2\tilde{I}_k(i_1)^2]\mathbb{E}[\tilde{I}_{j}(i_2)\tilde{I}_{k}(i_2)]+3\mathbb{E}[\tilde{I}_j(i_1)^3\tilde{I}_k(i_1)]\mathbb{E}[\tilde{I}_{k}(i_2)^2]\Big\}\nonumber\\&\quad+3\mathbb{E}[\tilde{I}_k(i_1)^3\tilde{I}_j(i_1)]\mathbb{E}[\tilde{I}_{j}(i_2)^2]\nonumber\\&\quad+\sum_{i_1=1}^n\sum_{i_2\not=i_1}^n\sum_{i_3\not=i_1,i_2}^n\Big\{9\mathbb{E}[\tilde{I}_j(i_1)^2]\mathbb{E}[\tilde{I}_j(i_2)\tilde{I}_{k}(i_2)]\mathbb{E}[\tilde{I}_{k}(i_3)^2]\nonumber\\&\quad+6\mathbb{E}[\tilde{I}_j(i_1)\tilde{I}_k(i_1)]\mathbb{E}[\tilde{I}_j(i_2)\tilde{I}_k(i_2)]\mathbb{E}[\tilde{I}_j(i_3)\tilde{I}_k(i_3)]\Big\}\Bigg\}.\end{align}
We now calculate the expectations in the above expression. We have that
![]() $\mathbb{E}[\tilde{I}_{j}(i_2)^2]=\mathrm{Var}(I_j(i_2))=p_j(1-p_j)$
. Also, by a routine calculation (or using a standard formula for the third central moment of the Bernoulli distribution), we have that
$\mathbb{E}[\tilde{I}_{j}(i_2)^2]=\mathrm{Var}(I_j(i_2))=p_j(1-p_j)$
. Also, by a routine calculation (or using a standard formula for the third central moment of the Bernoulli distribution), we have that
![]() $\mathbb{E}[\tilde{I}_j(i_1)^3]=p_j(1-p_j)(1-2p_j)$
. For the more complex expectations involving products of powers of
$\mathbb{E}[\tilde{I}_j(i_1)^3]=p_j(1-p_j)(1-2p_j)$
. For the more complex expectations involving products of powers of
![]() $\tilde{I}_j(i_1)$
and
$\tilde{I}_j(i_1)$
and
![]() $\tilde{I}_k(i_1)$
,
$\tilde{I}_k(i_1)$
,
![]() $j\not=k$
, we use the fact that each trial leads to a unique classification. For
$j\not=k$
, we use the fact that each trial leads to a unique classification. For
![]() $u,v\in\mathbb{N}$
,
$u,v\in\mathbb{N}$
,
 \begin{align*} \mathbb{E}[\tilde{I}_j(i_1)^u\tilde{I}_k(i_1)^v]&=\mathbb{E}[(I_j(i_1)-p_j)^u(I_k(i_1)-p_k)^v]\\ &=-p_j^u(1-p_k)^v\mathbb{P}(I_k(i_1)=1)-p_k^v(1-p_j)^u\mathbb{P}(I_j(i_1)=1)\\ &\quad+p_j^up_k^v\mathbb{P}(I_j(i_1)=I_k(i_1)=0) \\ &=-p_j^u(1-p_k)^vp_k-p_k^v(1-p_j)^up_j+p_j^up_k^v(1-p_j-p_k)\\ &=p_jp_k\big[{-}p_j^{u-1}(1-p_k)^v-p_k^{v-1}(1-p_j)^u+(1-p_j-p_k)p_j^{u-1}p_k^{v-2}\big].\end{align*}
\begin{align*} \mathbb{E}[\tilde{I}_j(i_1)^u\tilde{I}_k(i_1)^v]&=\mathbb{E}[(I_j(i_1)-p_j)^u(I_k(i_1)-p_k)^v]\\ &=-p_j^u(1-p_k)^v\mathbb{P}(I_k(i_1)=1)-p_k^v(1-p_j)^u\mathbb{P}(I_j(i_1)=1)\\ &\quad+p_j^up_k^v\mathbb{P}(I_j(i_1)=I_k(i_1)=0) \\ &=-p_j^u(1-p_k)^vp_k-p_k^v(1-p_j)^up_j+p_j^up_k^v(1-p_j-p_k)\\ &=p_jp_k\big[{-}p_j^{u-1}(1-p_k)^v-p_k^{v-1}(1-p_j)^u+(1-p_j-p_k)p_j^{u-1}p_k^{v-2}\big].\end{align*}
In the case
![]() $u=v=1$
, we have the simplification
$u=v=1$
, we have the simplification
![]() $\mathbb{E}[\tilde{I}_j(i_1)\tilde{I}_k(i_1)]=-p_jp_k$
. Substituting these formulas for the expectations present in (21) now gives us
$\mathbb{E}[\tilde{I}_j(i_1)\tilde{I}_k(i_1)]=-p_jp_k$
. Substituting these formulas for the expectations present in (21) now gives us
 \begin{align*} \mathbb{E}[S_j^3S_k^3]&=\frac{1}{n^3(p_jp_k)^{3/2}}\Big[n\cdot p_jp_k\big[{-}p_j^2(1-p_k)^3-p_k^2(1-p_j)^3+(1-p_j-p_k)(p_jp_k)^2\big]\\ &\quad+n(n-1)\Big\{\Big(p_jp_k(1-p_j)(1-p_k)(1-2p_j)(1-2p_k)\Big)\\ &\quad+9\Big((p_jp_k)^2\big[p_k(1-p_j)^2+p_j(1-p_k)^2+p_j+p_k-1\big]\Big)\\ &\quad+3\Big(p_jp_k^2(1-p_k)(1-2p_k)\big[1-p_j-p_k-p_j^2(1-p_k)-(1-p_j)^3\big]\Big)\\ &\quad+3\Big(p_j^2p_k(1-p_j)(1-2p_j)\big[1-p_k-p_j-p_k^2(1-p_j)-(1-p_k)^3\big]\Big)\Big\}\\ &\quad+n(n-1)(n-2)\Big\{9\Big({-}(p_jp_k)^2(1-p_j)(1-p_k)\Big)+6\Big({-}(p_jp_k)^3\Big)\Big\}\Big].\end{align*}
\begin{align*} \mathbb{E}[S_j^3S_k^3]&=\frac{1}{n^3(p_jp_k)^{3/2}}\Big[n\cdot p_jp_k\big[{-}p_j^2(1-p_k)^3-p_k^2(1-p_j)^3+(1-p_j-p_k)(p_jp_k)^2\big]\\ &\quad+n(n-1)\Big\{\Big(p_jp_k(1-p_j)(1-p_k)(1-2p_j)(1-2p_k)\Big)\\ &\quad+9\Big((p_jp_k)^2\big[p_k(1-p_j)^2+p_j(1-p_k)^2+p_j+p_k-1\big]\Big)\\ &\quad+3\Big(p_jp_k^2(1-p_k)(1-2p_k)\big[1-p_j-p_k-p_j^2(1-p_k)-(1-p_j)^3\big]\Big)\\ &\quad+3\Big(p_j^2p_k(1-p_j)(1-2p_j)\big[1-p_k-p_j-p_k^2(1-p_j)-(1-p_k)^3\big]\Big)\Big\}\\ &\quad+n(n-1)(n-2)\Big\{9\Big({-}(p_jp_k)^2(1-p_j)(1-p_k)\Big)+6\Big({-}(p_jp_k)^3\Big)\Big\}\Big].\end{align*}
Elementary calculations that make use of the facts that
![]() $p_j,p_k\in(0,1)$
and that
$p_j,p_k\in(0,1)$
and that
![]() $0\leq p_j+p_k\leq 1$
now yield the bound
$0\leq p_j+p_k\leq 1$
now yield the bound
 \begin{align} \big|\mathbb{E}[S_j^3S_k^3]\big| & \leq \frac{1}{n^3(p_jp_k)^{3/2}}\Big\{np_jp_k+n^2p_jp_k+9n^2(p_jp_k)^2+3n^2p_jp_k^2+3n^2p_j^2p_k\nonumber\\ &\quad+9n^3(p_jp_k)^2+6n^3(p_jp_k)^3\Big\} \nonumber\\ &=\frac{1}{n^2\sqrt{p_jp_k}\,}+\frac{1}{4n\sqrt{p_jp_k}\,}+\frac{9\sqrt{p_jp_k}}{n}+\frac{3p_k^{3/2}}{n\sqrt{p_j}\,}+\frac{3p_j^{3/2}}{n\sqrt{p_k}\,}+\frac{9}{4}\sqrt{p_jp_k}+6(p_jp_k)^{3/2}\nonumber\\ &=\frac{1}{n\cdot n\sqrt{p_jp_k}\,}+\frac{1}{4n\sqrt{p_jp_k}\,}+\frac{9p_jp_k}{n\sqrt{p_jp_k}\,}+\frac{3\sqrt{p_j}p_k^{3/2}}{np_j}+\frac{3p_j^{3/2}\sqrt{p_k}}{np_k}+\frac{9}{4}\sqrt{p_jp_k}\nonumber\\ &\quad+6(p_jp_k)\cdot\sqrt{p_jp_k}.\end{align}
\begin{align} \big|\mathbb{E}[S_j^3S_k^3]\big| & \leq \frac{1}{n^3(p_jp_k)^{3/2}}\Big\{np_jp_k+n^2p_jp_k+9n^2(p_jp_k)^2+3n^2p_jp_k^2+3n^2p_j^2p_k\nonumber\\ &\quad+9n^3(p_jp_k)^2+6n^3(p_jp_k)^3\Big\} \nonumber\\ &=\frac{1}{n^2\sqrt{p_jp_k}\,}+\frac{1}{4n\sqrt{p_jp_k}\,}+\frac{9\sqrt{p_jp_k}}{n}+\frac{3p_k^{3/2}}{n\sqrt{p_j}\,}+\frac{3p_j^{3/2}}{n\sqrt{p_k}\,}+\frac{9}{4}\sqrt{p_jp_k}+6(p_jp_k)^{3/2}\nonumber\\ &=\frac{1}{n\cdot n\sqrt{p_jp_k}\,}+\frac{1}{4n\sqrt{p_jp_k}\,}+\frac{9p_jp_k}{n\sqrt{p_jp_k}\,}+\frac{3\sqrt{p_j}p_k^{3/2}}{np_j}+\frac{3p_j^{3/2}\sqrt{p_k}}{np_k}+\frac{9}{4}\sqrt{p_jp_k}\nonumber\\ &\quad+6(p_jp_k)\cdot\sqrt{p_jp_k}.\end{align}
In obtaining this bound we did not attempt to optimise numerical constants, although in bounding the second and sixth terms we did take advantage of the simple inequality
![]() $(1-p_j)(1-p_k)\leq1/4$
(maximum at
$(1-p_j)(1-p_k)\leq1/4$
(maximum at
![]() $p_j=p_k=1/2$
). The final equality in (22) was given in anticipation of obtaining our final bound (20) for
$p_j=p_k=1/2$
). The final equality in (22) was given in anticipation of obtaining our final bound (20) for
![]() $\big|\mathbb{E}[S_j^3S_k^3]\big|$
. We now bound the terms in (22) using the following considerations. By assumption,
$\big|\mathbb{E}[S_j^3S_k^3]\big|$
. We now bound the terms in (22) using the following considerations. By assumption,
![]() $np_j\geq r$
for all
$np_j\geq r$
for all
![]() $j=1,\ldots,r$
, which also implies that
$j=1,\ldots,r$
, which also implies that
![]() $n\geq4$
, as
$n\geq4$
, as
![]() $r\geq2$
. Moreover, for
$r\geq2$
. Moreover, for
![]() $j\not=k$
,
$j\not=k$
,
![]() $p_jp_k\leq1/4$
(maximised for
$p_jp_k\leq1/4$
(maximised for
![]() $p_j=p_k=1/2$
) and
$p_j=p_k=1/2$
) and
![]() $\sqrt{p_j}p_k^{3/2}\leq3\sqrt{3}/16$
(maximised at
$\sqrt{p_j}p_k^{3/2}\leq3\sqrt{3}/16$
(maximised at
![]() $p_j=1/4$
,
$p_j=1/4$
,
![]() $p_k=3/4$
), with the same bound holding for
$p_k=3/4$
), with the same bound holding for
![]() $p_j^{3/2}\sqrt{p_k}$
by symmetry. With these considerations, we arrive at the bound
$p_j^{3/2}\sqrt{p_k}$
by symmetry. With these considerations, we arrive at the bound
where in obtaining the second inequality we rounded the numerical constants up to the nearest integer. The proof of the lemma is complete.
The following lemma, which is proved in Appendix B, will be needed in the proof of Theorem 2. Lemma 5 below will be needed in the proof of Theorem 3. The proof of Lemma 5 is similar to that of Lemma 4 and is given in the Supplementary Information.
Lemma 4. Let
![]() $a>0$
. Then,
$a>0$
. Then,
-
(i) For
 $x\geq0$
, (23)
$x\geq0$
, (23) \begin{equation} \bigg|2x\log\!\bigg(\frac{x}{a}\bigg)-2(x-a)-\frac{(x-a)^2}{a}+\frac{(x-a)^3}{3a^2}\bigg|\leq\frac{2(x-a)^4}{3a^3}. \end{equation}
\begin{equation} \bigg|2x\log\!\bigg(\frac{x}{a}\bigg)-2(x-a)-\frac{(x-a)^2}{a}+\frac{(x-a)^3}{3a^2}\bigg|\leq\frac{2(x-a)^4}{3a^3}. \end{equation}
-
(ii) Suppose
 $\lambda\geq3$
. Then, for
$\lambda\geq3$
. Then, for
 $x\geq0$
, (24)
$x\geq0$
, (24) \begin{multline} \bigg|\frac{x^{\lambda+1}}{a^\lambda}-a-(\lambda+1)(x-a)-\frac{\lambda(\lambda+1)}{2a}(x-a)^2-\frac{(\lambda-1)\lambda(\lambda+1)}{6a^2}(x-a)^3\bigg| \\ \leq \frac{(\lambda-2)(\lambda-1)\lambda(\lambda+1)}{24}\bigg(1+\Big(\frac{x}{a}\Big)^{\lambda-3}\bigg)\frac{(x-a)^4}{a^3}. \end{multline}
\begin{multline} \bigg|\frac{x^{\lambda+1}}{a^\lambda}-a-(\lambda+1)(x-a)-\frac{\lambda(\lambda+1)}{2a}(x-a)^2-\frac{(\lambda-1)\lambda(\lambda+1)}{6a^2}(x-a)^3\bigg| \\ \leq \frac{(\lambda-2)(\lambda-1)\lambda(\lambda+1)}{24}\bigg(1+\Big(\frac{x}{a}\Big)^{\lambda-3}\bigg)\frac{(x-a)^4}{a^3}. \end{multline}
-
(iii) Suppose
 $\lambda\in({-}1,3)\setminus\{0\}$
. Then, for
$\lambda\in({-}1,3)\setminus\{0\}$
. Then, for
 $x\geq0$
, (25)
$x\geq0$
, (25) \begin{multline} \bigg|\frac{x^{\lambda+1}}{a^\lambda}-a-(\lambda+1)(x-a)-\frac{\lambda(\lambda+1)}{2a}(x-a)^2-\frac{(\lambda-1)\lambda(\lambda+1)}{6a^2}(x-a)^3\bigg| \\ \leq \frac{|(\lambda-2)(\lambda-1)\lambda|}{6}\frac{(x-a)^4}{a^3}. \end{multline}
\begin{multline} \bigg|\frac{x^{\lambda+1}}{a^\lambda}-a-(\lambda+1)(x-a)-\frac{\lambda(\lambda+1)}{2a}(x-a)^2-\frac{(\lambda-1)\lambda(\lambda+1)}{6a^2}(x-a)^3\bigg| \\ \leq \frac{|(\lambda-2)(\lambda-1)\lambda|}{6}\frac{(x-a)^4}{a^3}. \end{multline}
Lemma 5. Let
![]() $a>0$
. Then,
$a>0$
. Then,
-
(i) For
 $x\geq0$
, (26)
$x\geq0$
, (26) \begin{equation} \bigg|2x\log\!\bigg(\frac{x}{a}\bigg)-2(x-a)-\frac{(x-a)^2}{a}\bigg|\leq\frac{|x-a|^3}{a^2}. \end{equation}
\begin{equation} \bigg|2x\log\!\bigg(\frac{x}{a}\bigg)-2(x-a)-\frac{(x-a)^2}{a}\bigg|\leq\frac{|x-a|^3}{a^2}. \end{equation}
-
(ii) Suppose
 $\lambda\geq2$
. Then, for
$\lambda\geq2$
. Then, for
 $x\geq0$
, (27)
$x\geq0$
, (27) \begin{multline} \bigg|\frac{x^{\lambda+1}}{a^\lambda}-a-(\lambda+1)(x-a)-\frac{\lambda(\lambda+1)}{2a}(x-a)^2\bigg| \\ \leq \frac{(\lambda-1)\lambda(\lambda+1)}{6}\bigg(1+\Big(\frac{x}{a}\Big)^{\lambda-2}\bigg)\frac{|x-a|^3}{a^2}. \end{multline}
\begin{multline} \bigg|\frac{x^{\lambda+1}}{a^\lambda}-a-(\lambda+1)(x-a)-\frac{\lambda(\lambda+1)}{2a}(x-a)^2\bigg| \\ \leq \frac{(\lambda-1)\lambda(\lambda+1)}{6}\bigg(1+\Big(\frac{x}{a}\Big)^{\lambda-2}\bigg)\frac{|x-a|^3}{a^2}. \end{multline}
-
(iii) Suppose
 $\lambda\in({-}1,2)\setminus\{0\}$
. Then, for
$\lambda\in({-}1,2)\setminus\{0\}$
. Then, for
 $x\geq0$
, (28)
$x\geq0$
, (28) \begin{align} \bigg|\frac{x^{\lambda+1}}{a^\lambda}-a-(\lambda+1)(x-a)-\frac{\lambda(\lambda+1)}{2a}(x-a)^2\bigg|\leq \frac{|(\lambda-1)\lambda|}{2}\frac{|x-a|^3}{a^2}. \end{align}
\begin{align} \bigg|\frac{x^{\lambda+1}}{a^\lambda}-a-(\lambda+1)(x-a)-\frac{\lambda(\lambda+1)}{2a}(x-a)^2\bigg|\leq \frac{|(\lambda-1)\lambda|}{2}\frac{|x-a|^3}{a^2}. \end{align}
4. Proofs of main results
In this section we prove all the results stated in Section 2, except for Theorem 1, which is proved in Appendix A. We begin by introducing some notation and make some basic observations regarding the power divergence statistic
![]() $T_\lambda$
.
$T_\lambda$
.
For
![]() $j=1,\ldots,r$
, let
$j=1,\ldots,r$
, let
![]() $S_j=(U_j-np_j)/\sqrt{np_j}$
denote the standardised cell counts, and let
$S_j=(U_j-np_j)/\sqrt{np_j}$
denote the standardised cell counts, and let
![]() $\boldsymbol{S}=(S_1,\ldots,S_r)^\top$
. Observe that
$\boldsymbol{S}=(S_1,\ldots,S_r)^\top$
. Observe that
![]() $\sum_{j=1}^rU_j=n$
and
$\sum_{j=1}^rU_j=n$
and
![]() $\sum_{j=1}^r\sqrt{p_j}S_j=0$
, and that
$\sum_{j=1}^r\sqrt{p_j}S_j=0$
, and that
![]() $U_j\sim\mathrm{Bin}(n,p_j)$
,
$U_j\sim\mathrm{Bin}(n,p_j)$
,
![]() $j=1,\ldots,r$
. With this notation, we may write the power divergence statistic
$j=1,\ldots,r$
. With this notation, we may write the power divergence statistic
![]() $T_\lambda$
, Pearson’s statistic
$T_\lambda$
, Pearson’s statistic
![]() $\chi^2$
, and the likelihood ratio statistic L as
$\chi^2$
, and the likelihood ratio statistic L as
 \begin{align*} T_\lambda & =\frac{2}{\lambda(\lambda+1)}\bigg[\sum_{j=1}^rnp_j\bigg(1+\frac{S_j}{\sqrt{np_j}\,}\bigg)^{\lambda+1}-n\bigg], \qquad \chi^2 =\sum_{j=1}^r S_j^2, \\ L&=T_0=2\sum_{j=1}^r\big(np_j+\sqrt{np_j}S_j\big)\log\!\bigg(1+\frac{S_j}{\sqrt{np_j}\,}\bigg).\end{align*}
\begin{align*} T_\lambda & =\frac{2}{\lambda(\lambda+1)}\bigg[\sum_{j=1}^rnp_j\bigg(1+\frac{S_j}{\sqrt{np_j}\,}\bigg)^{\lambda+1}-n\bigg], \qquad \chi^2 =\sum_{j=1}^r S_j^2, \\ L&=T_0=2\sum_{j=1}^r\big(np_j+\sqrt{np_j}S_j\big)\log\!\bigg(1+\frac{S_j}{\sqrt{np_j}\,}\bigg).\end{align*}
Proof of Theorem
2.For our purpose of deriving an order
![]() $n^{-1}$
bound, it will be convenient to write the power divergence statistic
$n^{-1}$
bound, it will be convenient to write the power divergence statistic
![]() $T_\lambda$
in the form
$T_\lambda$
in the form
 \begin{equation*} T_\lambda=\sum_{j=1}^rS_j^2+\frac{\lambda-1}{3}\sum_{j=1}^r\frac{S_j^3}{\sqrt{np_j}\,}+R_\lambda(\boldsymbol{S}),\end{equation*}
\begin{equation*} T_\lambda=\sum_{j=1}^rS_j^2+\frac{\lambda-1}{3}\sum_{j=1}^r\frac{S_j^3}{\sqrt{np_j}\,}+R_\lambda(\boldsymbol{S}),\end{equation*}
where, for
![]() $\lambda\in({-}1,\infty)\setminus\{0\}$
,
$\lambda\in({-}1,\infty)\setminus\{0\}$
,
 \begin{align*} R_\lambda(\boldsymbol{S})&=\frac{2}{\lambda(\lambda+1)}\sum_{j=1}^r\bigg[np_j\bigg(1+\frac{S_j}{\sqrt{np_j}\,}\bigg)^{\lambda+1}-np_j-(\lambda+1)\sqrt{np_j}S_j-\frac{\lambda(\lambda+1)}{2}S_j^2\\ &\quad-\frac{(\lambda-1)\lambda(\lambda+1)}{6\sqrt{np_j}}S_j^3\bigg],\end{align*}
\begin{align*} R_\lambda(\boldsymbol{S})&=\frac{2}{\lambda(\lambda+1)}\sum_{j=1}^r\bigg[np_j\bigg(1+\frac{S_j}{\sqrt{np_j}\,}\bigg)^{\lambda+1}-np_j-(\lambda+1)\sqrt{np_j}S_j-\frac{\lambda(\lambda+1)}{2}S_j^2\\ &\quad-\frac{(\lambda-1)\lambda(\lambda+1)}{6\sqrt{np_j}}S_j^3\bigg],\end{align*}
and, for
![]() $\lambda=0$
,
$\lambda=0$
,
 \begin{align*} R_0(\boldsymbol{S})&=\sum_{j=1}^r\bigg[2\big(np_j+\sqrt{np_j}S_j\big)\log\!\bigg(1+\frac{S_j}{\sqrt{np_j}\,}\bigg)-2\sqrt{np_j}S_j-S_j^2-\frac{S_j^3}{3\sqrt{np_j}\,}\bigg].\end{align*}
\begin{align*} R_0(\boldsymbol{S})&=\sum_{j=1}^r\bigg[2\big(np_j+\sqrt{np_j}S_j\big)\log\!\bigg(1+\frac{S_j}{\sqrt{np_j}\,}\bigg)-2\sqrt{np_j}S_j-S_j^2-\frac{S_j^3}{3\sqrt{np_j}\,}\bigg].\end{align*}
Here we used that
![]() $\sum_{j=1}^rp_j=1$
and
$\sum_{j=1}^rp_j=1$
and
![]() $\sum_{j=1}^r\sqrt{p_j}S_j=0$
.
$\sum_{j=1}^r\sqrt{p_j}S_j=0$
.
Let us now bound the quantity of interest,
![]() $\big|\mathbb{E}[h(T_\lambda)]-\chi_{(r-1)}^2h\big|$
. By a first-order Taylor expansion and the triangle inequality we have that
$\big|\mathbb{E}[h(T_\lambda)]-\chi_{(r-1)}^2h\big|$
. By a first-order Taylor expansion and the triangle inequality we have that
 \begin{align*} \big|\mathbb{E}[h(T_\lambda)]-\chi_{(r-1)}^2h \big| & = \Bigg|\mathbb{E}\Bigg[h\Bigg(\!\sum_{j=1}^rS_j^2+\frac{\lambda-1}{3}\sum_{j=1}^r\frac{S_j^3}{\sqrt{np_j}\,}+R_\lambda(\boldsymbol{S})\Bigg)\Bigg]-\chi_{(r-1)}^2h\Bigg|\\&\leq\Bigg|\mathbb{E}\Bigg[h\Bigg(\!\sum_{j=1}^rS_j^2+\frac{\lambda-1}{3}\sum_{j=1}^r\frac{S_j^3}{\sqrt{np_j}\,}\Bigg)\Bigg]-\chi_{(r-1)}^2h\Bigg|+R_1,\end{align*}
\begin{align*} \big|\mathbb{E}[h(T_\lambda)]-\chi_{(r-1)}^2h \big| & = \Bigg|\mathbb{E}\Bigg[h\Bigg(\!\sum_{j=1}^rS_j^2+\frac{\lambda-1}{3}\sum_{j=1}^r\frac{S_j^3}{\sqrt{np_j}\,}+R_\lambda(\boldsymbol{S})\Bigg)\Bigg]-\chi_{(r-1)}^2h\Bigg|\\&\leq\Bigg|\mathbb{E}\Bigg[h\Bigg(\!\sum_{j=1}^rS_j^2+\frac{\lambda-1}{3}\sum_{j=1}^r\frac{S_j^3}{\sqrt{np_j}\,}\Bigg)\Bigg]-\chi_{(r-1)}^2h\Bigg|+R_1,\end{align*}
where
![]() $R_1=\|h^{\prime}\|\mathbb{E}|R_\lambda(\boldsymbol{S})|$
. Another Taylor expansion and application of the triangle inequality gives us the bound
$R_1=\|h^{\prime}\|\mathbb{E}|R_\lambda(\boldsymbol{S})|$
. Another Taylor expansion and application of the triangle inequality gives us the bound
![]() $\big|\mathbb{E}[h(T_\lambda)]-\chi_{(r-1)}^2h\big|\leq R_1+R_2+R_3+R_4$
, where
$\big|\mathbb{E}[h(T_\lambda)]-\chi_{(r-1)}^2h\big|\leq R_1+R_2+R_3+R_4$
, where
 \begin{align*} R_2 & = \big|\mathbb{E}[h(\chi^2)]-\chi_{(r-1)}^2h\big|, \\ R_3 & = \frac{|\lambda-1|}{3}\Bigg|\mathbb{E}\Bigg[\sum_{j=1}^r\frac{S_j^3}{\sqrt{np_j}\,}h^{\prime}\Bigg(\!\sum_{k=1}^rS_k^2\Bigg)\Bigg]\Bigg|, \\ R_4 & = \frac{(\lambda-1)^2}{18}\|h^{\prime\prime}\|\mathbb{E}\Bigg[\Bigg(\!\sum_{j=1}^r\frac{S_j^3}{\sqrt{np_j}\,}\Bigg)^2\Bigg],\end{align*}
\begin{align*} R_2 & = \big|\mathbb{E}[h(\chi^2)]-\chi_{(r-1)}^2h\big|, \\ R_3 & = \frac{|\lambda-1|}{3}\Bigg|\mathbb{E}\Bigg[\sum_{j=1}^r\frac{S_j^3}{\sqrt{np_j}\,}h^{\prime}\Bigg(\!\sum_{k=1}^rS_k^2\Bigg)\Bigg]\Bigg|, \\ R_4 & = \frac{(\lambda-1)^2}{18}\|h^{\prime\prime}\|\mathbb{E}\Bigg[\Bigg(\!\sum_{j=1}^r\frac{S_j^3}{\sqrt{np_j}\,}\Bigg)^2\Bigg],\end{align*}
and we recall that Pearson’s statistic is given by
![]() $\chi^2=\sum_{j=1}^rS_j^2$
.
$\chi^2=\sum_{j=1}^rS_j^2$
.
We can bound the remainder
![]() $R_2$
immediately using either (4) or (6). To bound
$R_2$
immediately using either (4) or (6). To bound
![]() $R_3$
, we recall another bound of [Reference Gaunt, Pickett and Reinert14] (see the bound for
$R_3$
, we recall another bound of [Reference Gaunt, Pickett and Reinert14] (see the bound for
![]() $|\mathbb{E}h_2(\boldsymbol{S})|$
given on p. 747): for
$|\mathbb{E}h_2(\boldsymbol{S})|$
given on p. 747): for
![]() $j=1,\ldots,r$
,
$j=1,\ldots,r$
,
 \begin{equation*} \Bigg|\mathbb{E}\Bigg[S_j^3h^{\prime}\Bigg(\!\sum_{k=1}^rS_k^2\Bigg)\Bigg]\Bigg|\leq\big\{2\|h^{\prime}\|+202\|h^{\prime\prime}\|+819\|h^{(3)}\|+100\,974\|h^{(4)}\|\big\}\sum_{k=1}^r\frac{1}{\sqrt{np_k}\,}.\end{equation*}
\begin{equation*} \Bigg|\mathbb{E}\Bigg[S_j^3h^{\prime}\Bigg(\!\sum_{k=1}^rS_k^2\Bigg)\Bigg]\Bigg|\leq\big\{2\|h^{\prime}\|+202\|h^{\prime\prime}\|+819\|h^{(3)}\|+100\,974\|h^{(4)}\|\big\}\sum_{k=1}^r\frac{1}{\sqrt{np_k}\,}.\end{equation*}
Using this inequality. we obtain the bound
 \begin{equation*} R_3\leq\frac{|\lambda-1|}{3n}\Bigg(\!\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}\Bigg)^2\big\{2\|h^{\prime}\|+202\|h^{\prime\prime}\|+819\|h^{(3)}\|+100\,974\|h^{(4)}\|\big\}.\end{equation*}
\begin{equation*} R_3\leq\frac{|\lambda-1|}{3n}\Bigg(\!\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}\Bigg)^2\big\{2\|h^{\prime}\|+202\|h^{\prime\prime}\|+819\|h^{(3)}\|+100\,974\|h^{(4)}\|\big\}.\end{equation*}
Let us now bound
![]() $R_4$
. Using the moment bounds (18) and (20) (our assumption that
$R_4$
. Using the moment bounds (18) and (20) (our assumption that
![]() $np_j\geq r$
for all
$np_j\geq r$
for all
![]() $j=1,\ldots r$
allows us to apply this bound) gives
$j=1,\ldots r$
allows us to apply this bound) gives
 \begin{align*} \mathbb{E}\Bigg[\Bigg(\!\sum_{j=1}^r\frac{S_j^3}{\sqrt{np_j}\,}\Bigg)^2\Bigg] & = \sum_{j=1}^r\frac{\mathbb{E}[S_j^6]}{np_j}+\sum_{j=1}^r\sum_{k\not= j}^r\frac{\mathbb{E}[S_j^3S_k^3]}{n\sqrt{p_jp_k}\,} \\&\leq\sum_{j=1}^r\frac{28}{np_j}+\sum_{j=1}^r\sum_{k\not= j}\bigg\{\frac{6}{nr\sqrt{p_jp_k}\,}+\frac{4}{n}\bigg\}\leq\frac{38}{nr}\Bigg(\!\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}\Bigg)^2.\end{align*}
\begin{align*} \mathbb{E}\Bigg[\Bigg(\!\sum_{j=1}^r\frac{S_j^3}{\sqrt{np_j}\,}\Bigg)^2\Bigg] & = \sum_{j=1}^r\frac{\mathbb{E}[S_j^6]}{np_j}+\sum_{j=1}^r\sum_{k\not= j}^r\frac{\mathbb{E}[S_j^3S_k^3]}{n\sqrt{p_jp_k}\,} \\&\leq\sum_{j=1}^r\frac{28}{np_j}+\sum_{j=1}^r\sum_{k\not= j}\bigg\{\frac{6}{nr\sqrt{p_jp_k}\,}+\frac{4}{n}\bigg\}\leq\frac{38}{nr}\Bigg(\!\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}\Bigg)^2.\end{align*}
Therefore,
 \begin{equation*} R_4\leq\frac{19(\lambda-1)^2}{9nr}\|h^{\prime\prime}\|\Bigg(\!\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}\Bigg)^2.\end{equation*}
\begin{equation*} R_4\leq\frac{19(\lambda-1)^2}{9nr}\|h^{\prime\prime}\|\Bigg(\!\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}\Bigg)^2.\end{equation*}
Lastly, we bound
![]() $R_1$
. We consider the cases
$R_1$
. We consider the cases
![]() $\lambda=0$
(the likelihood ratio statistic),
$\lambda=0$
(the likelihood ratio statistic),
![]() $\lambda\geq3$
, and
$\lambda\geq3$
, and
![]() $\lambda\in({-}1,3)\setminus\{0\}$
separately. Using that
$\lambda\in({-}1,3)\setminus\{0\}$
separately. Using that
![]() $S_j=(U_j-np_j)/\sqrt{np_j}$
and then applying inequality (23) of Lemma 4, we have that, for
$S_j=(U_j-np_j)/\sqrt{np_j}$
and then applying inequality (23) of Lemma 4, we have that, for
![]() $\lambda=0$
,
$\lambda=0$
,
 \begin{align} R_1&=\|h^{\prime}\|\mathbb{E}|R_0(\boldsymbol{S})|\nonumber\\ &=\|h^{\prime}\|\mathbb{E}\Bigg|\sum_{j=1}^r\bigg[2U_j\log\!\bigg(\frac{U_j}{np_j}\bigg)-2(U_j-np_j)-\frac{(U_j-np_j)^2}{np_j}+\frac{(U_j-np_j)^3}{3(np_j)^2}\bigg]\Bigg|\nonumber\\ &\leq\frac{2\|h^{\prime}\|}{3}\sum_{j=1}^r\frac{\mathbb{E}[(U_j-np_j)^4]}{(np_j)^3}\leq\frac{8\|h^{\prime}\|}{3}\sum_{j=1}^r\frac{1}{np_j},\end{align}
\begin{align} R_1&=\|h^{\prime}\|\mathbb{E}|R_0(\boldsymbol{S})|\nonumber\\ &=\|h^{\prime}\|\mathbb{E}\Bigg|\sum_{j=1}^r\bigg[2U_j\log\!\bigg(\frac{U_j}{np_j}\bigg)-2(U_j-np_j)-\frac{(U_j-np_j)^2}{np_j}+\frac{(U_j-np_j)^3}{3(np_j)^2}\bigg]\Bigg|\nonumber\\ &\leq\frac{2\|h^{\prime}\|}{3}\sum_{j=1}^r\frac{\mathbb{E}[(U_j-np_j)^4]}{(np_j)^3}\leq\frac{8\|h^{\prime}\|}{3}\sum_{j=1}^r\frac{1}{np_j},\end{align}
where we used that
![]() $\mathbb{E}[(U_j-np_j)^4]\leq4(np_j)^2$
in the final step (see (17)).
$\mathbb{E}[(U_j-np_j)^4]\leq4(np_j)^2$
in the final step (see (17)).
Suppose now that
![]() $\lambda\geq3$
. Applying inequality (24) of Lemma 4, we have, for
$\lambda\geq3$
. Applying inequality (24) of Lemma 4, we have, for
![]() $\lambda\geq3$
,
$\lambda\geq3$
,
 \begin{align} R_1 & = \|h^{\prime}\|\mathbb{E}|R_\lambda(\boldsymbol{S})|\nonumber\\ &=\frac{2\|h^{\prime}\|}{\lambda(\lambda+1)}\mathbb{E}\Bigg|\sum_{j=1}^r\bigg[\frac{U_j^{\lambda+1}}{(np_j)^\lambda}-np_j-(\lambda+1)(U_j-np_j)-\frac{\lambda(\lambda+1)}{2}\frac{(U_j-np_j)^2}{np_j}\nonumber\\ &\quad-\frac{(\lambda-1)\lambda(\lambda+1)}{6}\frac{(U_j-np_j)^3}{(np_j)^2}\bigg]\Bigg|\end{align}
\begin{align} R_1 & = \|h^{\prime}\|\mathbb{E}|R_\lambda(\boldsymbol{S})|\nonumber\\ &=\frac{2\|h^{\prime}\|}{\lambda(\lambda+1)}\mathbb{E}\Bigg|\sum_{j=1}^r\bigg[\frac{U_j^{\lambda+1}}{(np_j)^\lambda}-np_j-(\lambda+1)(U_j-np_j)-\frac{\lambda(\lambda+1)}{2}\frac{(U_j-np_j)^2}{np_j}\nonumber\\ &\quad-\frac{(\lambda-1)\lambda(\lambda+1)}{6}\frac{(U_j-np_j)^3}{(np_j)^2}\bigg]\Bigg|\end{align}
 \begin{align} &\leq\frac{(\lambda-2)(\lambda-1)\|h^{\prime}\|}{12}\sum_{j=1}^r\mathbb{E}\bigg[\bigg(1+\frac{U_j^{\lambda-3}}{(np_j)^{\lambda-3}}\bigg)\frac{(U_j-np_j)^4}{(np_j)^3}\bigg]\nonumber\\ &\leq\frac{(\lambda-2)(\lambda-1)\|h^{\prime}\|}{12}\sum_{j=1}^r\bigg\{\frac{\mathbb{E}[(U_j-np_j)^4]}{(np_j)^3}\nonumber\\ &\quad+\frac{1}{(np_j)^{\lambda}}\big(\mathbb{E}\big[(U_j-np_j)^6\big]\big)^{2/3}\big(\mathbb{E}[U_j^{3\lambda-9}]\big)^{1/3}\bigg\}\nonumber\\ &\leq\frac{(\lambda-2)(\lambda-1)\|h^{\prime}\|}{12}\sum_{j=1}^r\bigg\{\frac{4}{np_j}+\frac{28^{2/3}\times (\mathrm{e}^{9/4})^{1/3}}{np_j}\bigg\}\nonumber\\ &\leq 2(\lambda-2)(\lambda-1)\|h^{\prime}\|\sum_{j=1}^r\frac{1}{np_j}.\end{align}
\begin{align} &\leq\frac{(\lambda-2)(\lambda-1)\|h^{\prime}\|}{12}\sum_{j=1}^r\mathbb{E}\bigg[\bigg(1+\frac{U_j^{\lambda-3}}{(np_j)^{\lambda-3}}\bigg)\frac{(U_j-np_j)^4}{(np_j)^3}\bigg]\nonumber\\ &\leq\frac{(\lambda-2)(\lambda-1)\|h^{\prime}\|}{12}\sum_{j=1}^r\bigg\{\frac{\mathbb{E}[(U_j-np_j)^4]}{(np_j)^3}\nonumber\\ &\quad+\frac{1}{(np_j)^{\lambda}}\big(\mathbb{E}\big[(U_j-np_j)^6\big]\big)^{2/3}\big(\mathbb{E}[U_j^{3\lambda-9}]\big)^{1/3}\bigg\}\nonumber\\ &\leq\frac{(\lambda-2)(\lambda-1)\|h^{\prime}\|}{12}\sum_{j=1}^r\bigg\{\frac{4}{np_j}+\frac{28^{2/3}\times (\mathrm{e}^{9/4})^{1/3}}{np_j}\bigg\}\nonumber\\ &\leq 2(\lambda-2)(\lambda-1)\|h^{\prime}\|\sum_{j=1}^r\frac{1}{np_j}.\end{align}
Here we used Hölder’s inequality to obtain the second inequality; to get the third inequality we used the moment bounds (17), (18), and (19), respectively,
![]() $\mathbb{E}\big[(U_j-np_j)^4\big]\leq4(np_j)^2$
,
$\mathbb{E}\big[(U_j-np_j)^4\big]\leq4(np_j)^2$
,
![]() $\mathbb{E}\big[(U_j-np_j)^6\big]\leq28(np_j)^3$
, and
$\mathbb{E}\big[(U_j-np_j)^6\big]\leq28(np_j)^3$
, and
![]() $\mathbb{E}[U_j^{3\lambda-9}]\leq \mathrm{e}^{9/4}(np_j)^{3\lambda-9}$
, where the latter bound is valid due to our assumption that
$\mathbb{E}[U_j^{3\lambda-9}]\leq \mathrm{e}^{9/4}(np_j)^{3\lambda-9}$
, where the latter bound is valid due to our assumption that
![]() $np_*\geq2(\lambda-3)^2$
for
$np_*\geq2(\lambda-3)^2$
for
![]() $\lambda\geq3$
.
$\lambda\geq3$
.
Lastly, we consider the case
![]() $\lambda\in({-}1,3)\setminus\{0\}$
. Applying inequality (25) of Lemma 4 to (30) and proceeding as before gives that, for
$\lambda\in({-}1,3)\setminus\{0\}$
. Applying inequality (25) of Lemma 4 to (30) and proceeding as before gives that, for
![]() $\lambda\in({-}1,3)\setminus\{0\}$
,
$\lambda\in({-}1,3)\setminus\{0\}$
,
 \begin{align} R_1\leq\frac{|(\lambda-2)(\lambda-1)|\|h^{\prime}\|}{6(\lambda+1)}\sum_{j=1}^r\frac{\mathbb{E}[(U_j-np_j)^4]}{(np_j)^3}\leq \frac{2|(\lambda-2)(\lambda-1)|\|h^{\prime}\|}{3(\lambda+1)}\sum_{j=1}^r\frac{1}{np_j}.\end{align}
\begin{align} R_1\leq\frac{|(\lambda-2)(\lambda-1)|\|h^{\prime}\|}{6(\lambda+1)}\sum_{j=1}^r\frac{\mathbb{E}[(U_j-np_j)^4]}{(np_j)^3}\leq \frac{2|(\lambda-2)(\lambda-1)|\|h^{\prime}\|}{3(\lambda+1)}\sum_{j=1}^r\frac{1}{np_j}.\end{align}
To obtain a universal bound on
![]() $\big|\mathbb{E}[h(T_\lambda)]-\chi_{(r-1)}^2h\big|$
that is valid for all
$\big|\mathbb{E}[h(T_\lambda)]-\chi_{(r-1)}^2h\big|$
that is valid for all
![]() $\lambda>-1$
, we observe that we can take the following upper bound for
$\lambda>-1$
, we observe that we can take the following upper bound for
![]() $R_1$
(valid for
$R_1$
(valid for
![]() $\lambda\geq3$
under the condition that
$\lambda\geq3$
under the condition that
![]() $np_*\geq 2(\lambda-3)^2$
),
$np_*\geq 2(\lambda-3)^2$
),
 \begin{align} R_1\leq\frac{|(\lambda-1)(\lambda-2)(12\lambda+13)|\|h^{\prime}\|}{6(\lambda+1)}\sum_{j=1}^r\frac{1}{np_j},\end{align}
\begin{align} R_1\leq\frac{|(\lambda-1)(\lambda-2)(12\lambda+13)|\|h^{\prime}\|}{6(\lambda+1)}\sum_{j=1}^r\frac{1}{np_j},\end{align}
which can be seen to be greater than each of the upper bounds (29), (31), and (32) that were obtained for the cases
![]() $\lambda=0$
,
$\lambda=0$
,
![]() $\lambda\geq3$
, and
$\lambda\geq3$
, and
![]() $\lambda\in({-}1,3)\setminus\{0\}$
, respectively.
$\lambda\in({-}1,3)\setminus\{0\}$
, respectively.
Finally, we sum up our bound in (33) for
![]() $R_1$
and our bounds for
$R_1$
and our bounds for
![]() $R_2$
,
$R_2$
,
![]() $R_3$
, and
$R_3$
, and
![]() $R_4$
. To obtain a compact final bound we use the inequality
$R_4$
. To obtain a compact final bound we use the inequality
![]() $\big(\!\sum_{j=1}^rp_j^{-1/2}\big)^2\leq r\sum_{j=1}^rp_j^{-1}$
, which follows from the Cauchy–Schwarz inequality. Using (4) to bound
$\big(\!\sum_{j=1}^rp_j^{-1/2}\big)^2\leq r\sum_{j=1}^rp_j^{-1}$
, which follows from the Cauchy–Schwarz inequality. Using (4) to bound
![]() $R_2$
gives us the bound in (10), while using (6) to bound
$R_2$
gives us the bound in (10), while using (6) to bound
![]() $R_2$
yields (11). This completes the proof.
$R_2$
yields (11). This completes the proof.
Remark 6. It was a fortunate accident that the term
![]() $R_3$
had previously been bounded in [Reference Gaunt, Pickett and Reinert14]. That this term is
$R_3$
had previously been bounded in [Reference Gaunt, Pickett and Reinert14]. That this term is
![]() $O(n^{-1})$
is in some sense the key reason as to why the
$O(n^{-1})$
is in some sense the key reason as to why the
![]() $O(n^{-1})$
rate is attained. Indeed, through our use of Taylor expansions we could guarantee that the remainder terms
$O(n^{-1})$
rate is attained. Indeed, through our use of Taylor expansions we could guarantee that the remainder terms
![]() $R_1$
and
$R_1$
and
![]() $R_4$
would be
$R_4$
would be
![]() $O(n^{-1})$
, and
$O(n^{-1})$
, and
![]() $R_2=\big|\mathbb{E}[h(\chi^2)]-\chi_{(r-1)}^2h\big|$
had, of course, already been shown to be
$R_2=\big|\mathbb{E}[h(\chi^2)]-\chi_{(r-1)}^2h\big|$
had, of course, already been shown to be
![]() $O(n^{-1})$
by [Reference Gaunt, Pickett and Reinert14]. To give a self-contained account as to why the
$O(n^{-1})$
by [Reference Gaunt, Pickett and Reinert14]. To give a self-contained account as to why the
![]() $O(n^{-1})$
rate is attained, we therefore briefly sketch why
$O(n^{-1})$
rate is attained, we therefore briefly sketch why
![]() $R_3=O(n^{-1})$
.
$R_3=O(n^{-1})$
.
Let
![]() $g(\boldsymbol{s})=\sum_{j=1}^r p_j^{-1/2}s_j^3h^{\prime}\big(\!\sum_{k=1}^r s_k^2\big)$
. Observe that
$g(\boldsymbol{s})=\sum_{j=1}^r p_j^{-1/2}s_j^3h^{\prime}\big(\!\sum_{k=1}^r s_k^2\big)$
. Observe that
![]() $g({-}\boldsymbol{s})=-g(\boldsymbol{s})$
. Now, let
$g({-}\boldsymbol{s})=-g(\boldsymbol{s})$
. Now, let
![]() $\boldsymbol{Z}$
be a centered r-dimensional multivariate normal random vector with covariance matrix equal to that of
$\boldsymbol{Z}$
be a centered r-dimensional multivariate normal random vector with covariance matrix equal to that of
![]() $\boldsymbol{S}$
. Then, because
$\boldsymbol{S}$
. Then, because
![]() $\boldsymbol{Z}=_\mathrm{d}-\boldsymbol{Z}$
, we have that
$\boldsymbol{Z}=_\mathrm{d}-\boldsymbol{Z}$
, we have that
![]() $\mathbb{E}[g(\boldsymbol{Z})]=-\mathbb{E}[g({-}\boldsymbol{Z})]=-\mathbb{E}[g(\boldsymbol{Z})]$
, so that
$\mathbb{E}[g(\boldsymbol{Z})]=-\mathbb{E}[g({-}\boldsymbol{Z})]=-\mathbb{E}[g(\boldsymbol{Z})]$
, so that
![]() $\mathbb{E}[g(\boldsymbol{Z})]=0$
. Therefore,
$\mathbb{E}[g(\boldsymbol{Z})]=0$
. Therefore,
The quantity
![]() $\big|\mathbb{E}[g(\boldsymbol{S})]-\mathbb{E}[g(\boldsymbol{Z})]\big|$
can then be bounded to order
$\big|\mathbb{E}[g(\boldsymbol{S})]-\mathbb{E}[g(\boldsymbol{Z})]\big|$
can then be bounded to order
![]() $O(n^{-1/2})$
by Stein’s method for multivariate normal approximation with polynomial growth rate test functions [Reference Gaunt13].
$O(n^{-1/2})$
by Stein’s method for multivariate normal approximation with polynomial growth rate test functions [Reference Gaunt13].
Proof of Theorem
3.The proof is similar to that of Theorem 2, but a little shorter and simpler. For our aim of obtaining an order
![]() $n^{-1/2}$
bound, we express
$n^{-1/2}$
bound, we express
![]() $T_\lambda$
in the form
$T_\lambda$
in the form
![]() $T_\lambda=\sum_{j=1}^rS_j^2+R_\lambda(\boldsymbol{S})=\chi^2+R_\lambda(\boldsymbol{S})$
, where, for
$T_\lambda=\sum_{j=1}^rS_j^2+R_\lambda(\boldsymbol{S})=\chi^2+R_\lambda(\boldsymbol{S})$
, where, for
![]() $\lambda\in({-}1,\infty)\setminus\{0\}$
,
$\lambda\in({-}1,\infty)\setminus\{0\}$
,
 \begin{align*} R_\lambda(\boldsymbol{S})&=\frac{2}{\lambda(\lambda+1)}\sum_{j=1}^r\bigg[np_j\bigg(1+\frac{S_j}{\sqrt{np_j}\,}\bigg)^{\lambda+1}-np_j-(\lambda+1)\sqrt{np_j}S_j-\frac{\lambda(\lambda+1)}{2}S_j^2\bigg] \end{align*}
\begin{align*} R_\lambda(\boldsymbol{S})&=\frac{2}{\lambda(\lambda+1)}\sum_{j=1}^r\bigg[np_j\bigg(1+\frac{S_j}{\sqrt{np_j}\,}\bigg)^{\lambda+1}-np_j-(\lambda+1)\sqrt{np_j}S_j-\frac{\lambda(\lambda+1)}{2}S_j^2\bigg] \end{align*}
and, for
![]() $\lambda=0$
,
$\lambda=0$
,
 \begin{align*} R_0(\boldsymbol{S})&=\sum_{j=1}^r\bigg[2\big(np_j+\sqrt{np_j}S_j\big)\log\!\bigg(1+\frac{S_j}{\sqrt{np_j}\,}\bigg)-2\sqrt{np_j}S_j-S_j^2\bigg].\end{align*}
\begin{align*} R_0(\boldsymbol{S})&=\sum_{j=1}^r\bigg[2\big(np_j+\sqrt{np_j}S_j\big)\log\!\bigg(1+\frac{S_j}{\sqrt{np_j}\,}\bigg)-2\sqrt{np_j}S_j-S_j^2\bigg].\end{align*}
Now, by a first-order Taylor expansion and the triangle inequality we have that
where
![]() $R_1=\|h^{\prime}\|\mathbb{E}|R_\lambda(\boldsymbol{S})|$
.
$R_1=\|h^{\prime}\|\mathbb{E}|R_\lambda(\boldsymbol{S})|$
.
The quantity
![]() $\big|\mathbb{E}[h(\chi^2)]-\chi_{(r-1)}^2h\big|$
can be immediately bounded using either (5) or (7). To bound
$\big|\mathbb{E}[h(\chi^2)]-\chi_{(r-1)}^2h\big|$
can be immediately bounded using either (5) or (7). To bound
![]() $R_1$
, we consider the cases
$R_1$
, we consider the cases
![]() $\lambda=0$
,
$\lambda=0$
,
![]() $\lambda\geq2$
, and
$\lambda\geq2$
, and
![]() $\lambda\in({-}1,2)\setminus\{0\}$
separately. For
$\lambda\in({-}1,2)\setminus\{0\}$
separately. For
![]() $\lambda=0$
, using inequality (26) of Lemma 5 we obtain the bound
$\lambda=0$
, using inequality (26) of Lemma 5 we obtain the bound
 \begin{align} R_1 &=\|h^{\prime}\|\mathbb{E}\Bigg|\sum_{j=1}^r\bigg[2U_j\log\!\bigg(\frac{U_j}{np_j}\bigg)-2(U_j-np_j)-\frac{(U_j-np_j)^2}{np_j}\bigg]\Bigg|\nonumber\\ &\leq\|h^{\prime}\|\sum_{j=1}^r\frac{\mathbb{E}[|U_j-np_j|^3]}{(np_j)^2}\leq 3\|h^{\prime}\|\sum_{j=1}^r\frac{1}{\sqrt{np_j}\,},\end{align}
\begin{align} R_1 &=\|h^{\prime}\|\mathbb{E}\Bigg|\sum_{j=1}^r\bigg[2U_j\log\!\bigg(\frac{U_j}{np_j}\bigg)-2(U_j-np_j)-\frac{(U_j-np_j)^2}{np_j}\bigg]\Bigg|\nonumber\\ &\leq\|h^{\prime}\|\sum_{j=1}^r\frac{\mathbb{E}[|U_j-np_j|^3]}{(np_j)^2}\leq 3\|h^{\prime}\|\sum_{j=1}^r\frac{1}{\sqrt{np_j}\,},\end{align}
where we used inequality (16) in the final step.
For
![]() $\lambda\geq2$
we use inequality (27) of Lemma 5 to get
$\lambda\geq2$
we use inequality (27) of Lemma 5 to get
 \begin{align} R_1&=\frac{2\|h^{\prime}\|}{\lambda(\lambda+1)}\mathbb{E}\Bigg|\sum_{j=1}^r\bigg[\frac{U_j^{\lambda+1}}{(np_j)^\lambda}-np_j-(\lambda+1)(U_j-np_j)-\frac{\lambda(\lambda+1)}{2}\frac{(U_j-np_j)^2}{np_j}\bigg]\Bigg|\nonumber\\ &\leq\frac{(\lambda-1)\|h^{\prime}\|}{3}\sum_{j=1}^r\mathbb{E}\bigg[\bigg(1+\frac{U_j^{\lambda-2}}{(np_j)^{\lambda-2}}\bigg)\frac{|U_j-np_j|^3}{(np_j)^2}\bigg]\nonumber\\ &\leq\frac{(\lambda-1)\|h^{\prime}\|}{3}\sum_{j=1}^r\bigg\{\frac{\mathbb{E}[|U_j-np_j|^3]}{(np_j)^2}+\frac{1}{(np_j)^{\lambda}}\big(\mathbb{E}\big[(U_j-np_j)^6\big]\big)^{1/2}\big(\mathbb{E}[U_j^{2\lambda-4}]\big)^{1/2}\bigg\}\nonumber\\ &\leq\frac{(\lambda-1)\|h^{\prime}\|}{3}\sum_{j=1}^r\bigg\{\frac{3}{\sqrt{np_j}\,}+\frac{28^{1/2}\times \mathrm{e}^{1/2}}{\sqrt{np_j}}\bigg\}\leq 4(\lambda-1)\|h^{\prime}\|\sum_{j=1}^r\frac{1}{\sqrt{np_j}\,}.\end{align}
\begin{align} R_1&=\frac{2\|h^{\prime}\|}{\lambda(\lambda+1)}\mathbb{E}\Bigg|\sum_{j=1}^r\bigg[\frac{U_j^{\lambda+1}}{(np_j)^\lambda}-np_j-(\lambda+1)(U_j-np_j)-\frac{\lambda(\lambda+1)}{2}\frac{(U_j-np_j)^2}{np_j}\bigg]\Bigg|\nonumber\\ &\leq\frac{(\lambda-1)\|h^{\prime}\|}{3}\sum_{j=1}^r\mathbb{E}\bigg[\bigg(1+\frac{U_j^{\lambda-2}}{(np_j)^{\lambda-2}}\bigg)\frac{|U_j-np_j|^3}{(np_j)^2}\bigg]\nonumber\\ &\leq\frac{(\lambda-1)\|h^{\prime}\|}{3}\sum_{j=1}^r\bigg\{\frac{\mathbb{E}[|U_j-np_j|^3]}{(np_j)^2}+\frac{1}{(np_j)^{\lambda}}\big(\mathbb{E}\big[(U_j-np_j)^6\big]\big)^{1/2}\big(\mathbb{E}[U_j^{2\lambda-4}]\big)^{1/2}\bigg\}\nonumber\\ &\leq\frac{(\lambda-1)\|h^{\prime}\|}{3}\sum_{j=1}^r\bigg\{\frac{3}{\sqrt{np_j}\,}+\frac{28^{1/2}\times \mathrm{e}^{1/2}}{\sqrt{np_j}}\bigg\}\leq 4(\lambda-1)\|h^{\prime}\|\sum_{j=1}^r\frac{1}{\sqrt{np_j}\,}.\end{align}
Here we used the Cauchy–Schwarz inequality to obtain the second inequality; to get the third inequality we used the moment bounds (16), (18), and (19), respectively,
![]() $\mathbb{E}\big[(U_j-np_j)^4\big]\leq4(np_j)^2$
,
$\mathbb{E}\big[(U_j-np_j)^4\big]\leq4(np_j)^2$
,
![]() $\mathbb{E}\big[(U_j-np_j)^6\big]\leq28(np_j)^3$
, and
$\mathbb{E}\big[(U_j-np_j)^6\big]\leq28(np_j)^3$
, and
![]() $\mathbb{E}[U_j^{2\lambda-4}]\leq \mathrm{e}(np_j)^{2\lambda-4}$
, where the latter bound is valid due to our assumption that
$\mathbb{E}[U_j^{2\lambda-4}]\leq \mathrm{e}(np_j)^{2\lambda-4}$
, where the latter bound is valid due to our assumption that
![]() $np_*\geq2(\lambda-2)^2$
for
$np_*\geq2(\lambda-2)^2$
for
![]() $\lambda\geq2$
.
$\lambda\geq2$
.
Lastly, we consider the case
![]() $\lambda\in({-}1,2)\setminus\{0\}$
. Using inequality (28) of Lemma 5 on (30) and proceeding as before gives that, for
$\lambda\in({-}1,2)\setminus\{0\}$
. Using inequality (28) of Lemma 5 on (30) and proceeding as before gives that, for
![]() $\lambda\in({-}1,2)\setminus\{0\}$
,
$\lambda\in({-}1,2)\setminus\{0\}$
,
 \begin{align} R_1\leq\frac{|\lambda-1|\|h^{\prime}\|}{\lambda+1}\sum_{j=1}^r\frac{\mathbb{E}[|U_j-np_j|^3]}{(np_j)^2}\leq \frac{3|\lambda-1|\|h^{\prime}\|}{\lambda+1}\sum_{j=1}^r\frac{1}{\sqrt{np_j}\,}.\end{align}
\begin{align} R_1\leq\frac{|\lambda-1|\|h^{\prime}\|}{\lambda+1}\sum_{j=1}^r\frac{\mathbb{E}[|U_j-np_j|^3]}{(np_j)^2}\leq \frac{3|\lambda-1|\|h^{\prime}\|}{\lambda+1}\sum_{j=1}^r\frac{1}{\sqrt{np_j}\,}.\end{align}
To obtain a universal bound on
![]() $\big|\mathbb{E}[h(T_\lambda)]-\chi_{(r-1)}^2h\big|$
that is valid for all
$\big|\mathbb{E}[h(T_\lambda)]-\chi_{(r-1)}^2h\big|$
that is valid for all
![]() $\lambda>-1$
, we observe that we can take the following upper bound for
$\lambda>-1$
, we observe that we can take the following upper bound for
![]() $R_1$
(valid for
$R_1$
(valid for
![]() $\lambda\geq2$
provided
$\lambda\geq2$
provided
![]() $np_*\geq 2(\lambda-2)^2$
),
$np_*\geq 2(\lambda-2)^2$
),
 \begin{equation} R_1\leq\frac{|(\lambda-1)(4\lambda+7)|\|h^{\prime}\|}{\lambda+1}\sum_{j=1}^r\frac{1}{\sqrt{np_j}\,},\end{equation}
\begin{equation} R_1\leq\frac{|(\lambda-1)(4\lambda+7)|\|h^{\prime}\|}{\lambda+1}\sum_{j=1}^r\frac{1}{\sqrt{np_j}\,},\end{equation}
which can be seen to be greater than each of the upper bounds (34), (35), and (36) that were obtained for the cases
![]() $\lambda=0$
,
$\lambda=0$
,
![]() $\lambda\geq2$
, and
$\lambda\geq2$
, and
![]() $\lambda\in({-}1,2)\setminus\{0\}$
, respectively.
$\lambda\in({-}1,2)\setminus\{0\}$
, respectively.
Summing up our bound (37) for
![]() $R_1$
and either the bound (5) or the bound (7) for
$R_1$
and either the bound (5) or the bound (7) for
![]() $\big|\mathbb{E}[h(\chi^2)]-\chi_{(r-1)}^2h\big|$
now yields the desired bounds (12) and (13), respectively.
$\big|\mathbb{E}[h(\chi^2)]-\chi_{(r-1)}^2h\big|$
now yields the desired bounds (12) and (13), respectively.
Proof of Corollary
1.Let
![]() $\alpha>0$
and, for fixed
$\alpha>0$
and, for fixed
![]() $z>0$
, define
$z>0$
, define
 \begin{equation*} h_\alpha(x)=\begin{cases} 1, & \: \mbox{if } x\leq z, \\1-2(x-z)^2/\alpha^2, & \: \mbox {if } z<x\leq z+\alpha/2, \\2(x-(z+\alpha))^2/\alpha^2, & \: \mbox {if } z+\alpha/2<x\leq z+\alpha, \\0, & \: \mbox {if } x\geq z+\alpha. \end{cases}\end{equation*}
\begin{equation*} h_\alpha(x)=\begin{cases} 1, & \: \mbox{if } x\leq z, \\1-2(x-z)^2/\alpha^2, & \: \mbox {if } z<x\leq z+\alpha/2, \\2(x-(z+\alpha))^2/\alpha^2, & \: \mbox {if } z+\alpha/2<x\leq z+\alpha, \\0, & \: \mbox {if } x\geq z+\alpha. \end{cases}\end{equation*}
Then
![]() $h^{\prime}_\alpha$
is Lipshitz with
$h^{\prime}_\alpha$
is Lipshitz with
![]() $\|h_\alpha\|=1$
,
$\|h_\alpha\|=1$
,
![]() $\|h^{\prime}_\alpha\|=2/\alpha$
, and
$\|h^{\prime}_\alpha\|=2/\alpha$
, and
![]() $\|h^{\prime\prime}_\alpha\|=4/\alpha^2$
. Let
$\|h^{\prime\prime}_\alpha\|=4/\alpha^2$
. Let
![]() $Y_{r-1}\sim\chi_{(r-1)}^2$
. Then, using (12), together with the basic inequality
$Y_{r-1}\sim\chi_{(r-1)}^2$
. Then, using (12), together with the basic inequality
![]() $\sum_{j=1}^rp_j^{-1/2}\leq r/\sqrt{p_*}$
, gives
$\sum_{j=1}^rp_j^{-1/2}\leq r/\sqrt{p_*}$
, gives
 \begin{align} &\mathbb{P}(T_\lambda\leq z)-\mathbb{P}(Y_{r-1}\leq z)\nonumber\\ &\leq \mathbb{E}[h_\alpha(T_\lambda)]-\mathbb{E}[h_\alpha(Y_{r-1})]+\mathbb{E}[h_\alpha(Y_{r-1})]-\mathbb{P}(Y_{r-1}\leq z)\nonumber \\ &\leq \frac{1}{\sqrt{np_*}\,}\bigg\{72\|h_\alpha\|+\bigg(552+\frac{|(\lambda-1)(4\lambda+7)|r}{\lambda+1}\bigg)\|h^{\prime}_\alpha\|+1008\|h^{\prime\prime}_\alpha\|\bigg\}\nonumber\\ &\quad+\mathbb{P}(z\leq Y_{r-1}\leq z+\alpha)\nonumber \\ &=\frac{1}{\sqrt{np_*}\,}\bigg\{72+\frac{1104}{\alpha}+\frac{|(\lambda-1)(4\lambda+7)|r}{(\lambda+1)\alpha}+\frac{4032}{\alpha^2}\bigg\}+\mathbb{P}(z\leq Y_{r-1}\leq z+\alpha).\end{align}
\begin{align} &\mathbb{P}(T_\lambda\leq z)-\mathbb{P}(Y_{r-1}\leq z)\nonumber\\ &\leq \mathbb{E}[h_\alpha(T_\lambda)]-\mathbb{E}[h_\alpha(Y_{r-1})]+\mathbb{E}[h_\alpha(Y_{r-1})]-\mathbb{P}(Y_{r-1}\leq z)\nonumber \\ &\leq \frac{1}{\sqrt{np_*}\,}\bigg\{72\|h_\alpha\|+\bigg(552+\frac{|(\lambda-1)(4\lambda+7)|r}{\lambda+1}\bigg)\|h^{\prime}_\alpha\|+1008\|h^{\prime\prime}_\alpha\|\bigg\}\nonumber\\ &\quad+\mathbb{P}(z\leq Y_{r-1}\leq z+\alpha)\nonumber \\ &=\frac{1}{\sqrt{np_*}\,}\bigg\{72+\frac{1104}{\alpha}+\frac{|(\lambda-1)(4\lambda+7)|r}{(\lambda+1)\alpha}+\frac{4032}{\alpha^2}\bigg\}+\mathbb{P}(z\leq Y_{r-1}\leq z+\alpha).\end{align}
It was shown in [Reference Gaunt, Pickett and Reinert14, p.754] that
 \begin{equation} \mathbb{P}(z\leq Y_{r-1}\leq z+\alpha)\leq \begin{cases} \displaystyle \sqrt{2\alpha/\pi}, & \: \mbox{if } r=2, \\ \alpha/2, & \: \mbox{if } r=3, \\ \displaystyle \frac{\alpha}{2\sqrt{\pi(r-3)}\,}, & \: \mbox {if } r\geq4. \end{cases}\end{equation}
\begin{equation} \mathbb{P}(z\leq Y_{r-1}\leq z+\alpha)\leq \begin{cases} \displaystyle \sqrt{2\alpha/\pi}, & \: \mbox{if } r=2, \\ \alpha/2, & \: \mbox{if } r=3, \\ \displaystyle \frac{\alpha}{2\sqrt{\pi(r-3)}\,}, & \: \mbox {if } r\geq4. \end{cases}\end{equation}
Upper bounds for the cases
![]() $r=2$
,
$r=2$
,
![]() $r=3$
, and
$r=3$
, and
![]() $r\geq 4$
follow on substituting inequality (39) into (38) and selecting a suitable
$r\geq 4$
follow on substituting inequality (39) into (38) and selecting a suitable
![]() $\alpha$
. We choose
$\alpha$
. We choose
![]() $\alpha=52.75(np_*)^{-1/5}$
for
$\alpha=52.75(np_*)^{-1/5}$
for
![]() $r=2$
; we take
$r=2$
; we take
![]() $\alpha=25.27(np_*)^{-1/6}$
when
$\alpha=25.27(np_*)^{-1/6}$
when
![]() $r=3$
; and
$r=3$
; and
![]() $\alpha=30.58(r-3)^{1/6}(np_*)^{-1/6}$
for
$\alpha=30.58(r-3)^{1/6}(np_*)^{-1/6}$
for
![]() $r\geq4$
. A lower bound can be obtained similarly, which is the negative of the upper bound. The proof is now complete.
$r\geq4$
. A lower bound can be obtained similarly, which is the negative of the upper bound. The proof is now complete.
Appendix A. Stein’s method for chi-square approximation and proof of Theorem 1
The first detailed study of Stein’s method for chi-square approximation was given in [Reference Luk21]. For further details on Stein’s method for chi-square approximation we refer the reader to [Reference Döbler and Peccati9, Reference Gaunt, Pickett and Reinert14, Reference Nourdin and Peccati24]. At the heart of Stein’s method for chi-square approximation is the following so-called Stein equation for the
![]() $\chi_{(p)}^2$
distribution (see [Reference Diaconis and Zabell8]),
$\chi_{(p)}^2$
distribution (see [Reference Diaconis and Zabell8]),
where h is a real-valued test function and we recall that
![]() $\chi_{(d)}^2h$
denotes the quantity
$\chi_{(d)}^2h$
denotes the quantity
![]() $\mathbb{E}[h(Y_{p})]$
for
$\mathbb{E}[h(Y_{p})]$
for
![]() $Y_p\sim\chi_{(p)}^2$
. It is straightforward to verify that
$Y_p\sim\chi_{(p)}^2$
. It is straightforward to verify that
where
![]() $\rho(x)$
denotes the
$\rho(x)$
denotes the
![]() $\chi_{(p)}^2$
density, solves the Stein equation (40) (see [Reference Stein35, Lemma 1, p. 59]).
$\chi_{(p)}^2$
density, solves the Stein equation (40) (see [Reference Stein35, Lemma 1, p. 59]).
Suppose we wish to obtain error bounds for the approximation of the distribution of a random variable of interest W and a
![]() $\chi_{(p)}^2$
distribution. The Stein equation (40) allows us to obtain bounds on the quantity of interest
$\chi_{(p)}^2$
distribution. The Stein equation (40) allows us to obtain bounds on the quantity of interest
![]() $\big|\mathbb{E}[h(W)]-\chi_{(p)}^2h\big|$
by the following transfer principle: evaluate both sides of (40) at W and take expectations to obtain
$\big|\mathbb{E}[h(W)]-\chi_{(p)}^2h\big|$
by the following transfer principle: evaluate both sides of (40) at W and take expectations to obtain
where f is the solution (41). Thus, the chi-square approximation problem is reduced to bounding the right-hand side of (42). For this procedure to be effective, one requires suitable estimates for the solution of the Stein equation together with certain lower-order derivatives of the solution. We now record some bounds for solution (41) that will be needed in the proof of Theorem 1.
We first state a bound from [Reference Luk21]. For
![]() $h\in C_b^{k,k}(\mathbb{R}^+)$
,
$h\in C_b^{k,k}(\mathbb{R}^+)$
,
The following bound from [Reference Gaunt12] improved a bound from [Reference Pickett27]. For
![]() $h\in C_b^{k-1,k-1}(\mathbb{R}^+)$
,
$h\in C_b^{k-1,k-1}(\mathbb{R}^+)$
,
where
![]() $h^{(0)}\equiv h$
. The conditions on the test function h for the bounds (43) and (44) are the same (but presented in a simpler manner) as those used in [Reference Gaunt, Pickett and Reinert14], in which it was noted that the bounds are valid under these conditions which are weaker than those presented in [Reference Luk21] and [Reference Gaunt12]. From (44), we deduce (using that
$h^{(0)}\equiv h$
. The conditions on the test function h for the bounds (43) and (44) are the same (but presented in a simpler manner) as those used in [Reference Gaunt, Pickett and Reinert14], in which it was noted that the bounds are valid under these conditions which are weaker than those presented in [Reference Luk21] and [Reference Gaunt12]. From (44), we deduce (using that
![]() $p\geq1$
and
$p\geq1$
and
![]() $k\geq2$
) the simplified bounds
$k\geq2$
) the simplified bounds
and
Finally, we record a bound from [Reference Gaunt, Pickett and Reinert14]. For
![]() $h\in C_b^{k-2,k-1}(\mathbb{R}^+)$
,
$h\in C_b^{k-2,k-1}(\mathbb{R}^+)$
,
Proof of Theorem 1.In the proof of the bounds (4) and (5), [Reference Gaunt, Pickett and Reinert14] obtained the intermediate bounds
 \begin{align} \big|\mathbb{E}[h(\chi^2)]-\chi_{(r-1)}^2h\big| & \leq \frac{1}{n}\big\{19\|f^{\prime\prime}\|+309\|f^{(3)}\|+1089\|f^{(4)}\|\nonumber\\ &\quad+1997\|f^{(5)}\|+100\,974\|f^{(6)}\|\big\}\bigg(\!\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}\bigg)^2 \end{align}
\begin{align} \big|\mathbb{E}[h(\chi^2)]-\chi_{(r-1)}^2h\big| & \leq \frac{1}{n}\big\{19\|f^{\prime\prime}\|+309\|f^{(3)}\|+1089\|f^{(4)}\|\nonumber\\ &\quad+1997\|f^{(5)}\|+100\,974\|f^{(6)}\|\big\}\bigg(\!\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}\bigg)^2 \end{align}
and
 \begin{equation} \big|\mathbb{E}[h(\chi^2)]-\chi_{(r-1)}^2h\big| \leq \frac{1}{\sqrt{n}\,}\big\{18\|f^{\prime\prime}\|+84\|f^{(3)}\|\big\}\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}, \end{equation}
\begin{equation} \big|\mathbb{E}[h(\chi^2)]-\chi_{(r-1)}^2h\big| \leq \frac{1}{\sqrt{n}\,}\big\{18\|f^{\prime\prime}\|+84\|f^{(3)}\|\big\}\sum_{j=1}^r\frac{1}{\sqrt{p_j}\,}, \end{equation}
where f is the solution (41) of the
![]() $\chi_{(r-1)}^2$
Stein equation.
$\chi_{(r-1)}^2$
Stein equation.
We note that bounding the derivatives of the solution f of the
![]() $\chi_{(r-1)}^2$
Stein equation in (48) and (49) using inequality (47) then yields the bounds (4) and (5), respectively. The bounds (6) and (7) of Theorem 1 are obtained by instead using inequality (45) to bound the derivatives of f in the bounds (4) and (5), respectively. To get the bound (8) of Theorem 1, we use the inequality (43) to bound
$\chi_{(r-1)}^2$
Stein equation in (48) and (49) using inequality (47) then yields the bounds (4) and (5), respectively. The bounds (6) and (7) of Theorem 1 are obtained by instead using inequality (45) to bound the derivatives of f in the bounds (4) and (5), respectively. To get the bound (8) of Theorem 1, we use the inequality (43) to bound
![]() $\|f^{\prime\prime}\|,\ldots,\|f^{(5)}\|$
and (46) to bound
$\|f^{\prime\prime}\|,\ldots,\|f^{(5)}\|$
and (46) to bound
![]() $\|f^{(6)}\|$
in (48). Finally, to obtain the bound (9) we use (43) to bound
$\|f^{(6)}\|$
in (48). Finally, to obtain the bound (9) we use (43) to bound
![]() $\|f^{\prime\prime}\|$
and (46) to bound
$\|f^{\prime\prime}\|$
and (46) to bound
![]() $\|f^{(3)}\|$
in (49).
$\|f^{(3)}\|$
in (49).
Appendix B. Proof of Lemma 4
Proof of Lemma
4.(i) Without loss of generality, we let
![]() $a=1$
; the general
$a=1$
; the general
![]() $a>0$
case follows by rescaling. We therefore need to prove that, for
$a>0$
case follows by rescaling. We therefore need to prove that, for
![]() $x\geq0$
,
$x\geq0$
,
where
![]() $f(x)\,:\!=\,2x\log\!(x)-2(x-1)-(x-1)^2+\frac{1}{3}(x-1)^3$
. It is readily checked that inequality (50) holds for
$f(x)\,:\!=\,2x\log\!(x)-2(x-1)-(x-1)^2+\frac{1}{3}(x-1)^3$
. It is readily checked that inequality (50) holds for
![]() $x=0$
and
$x=0$
and
![]() $x=2$
. For
$x=2$
. For
![]() $0<x<2$
(i.e.
$0<x<2$
(i.e.
![]() $|x-1|<1$
), we can use a Taylor expansion to obtain the bound
$|x-1|<1$
), we can use a Taylor expansion to obtain the bound
so inequality (50) is satisfied for
![]() $0<x<2$
. Now, suppose
$0<x<2$
. Now, suppose
![]() $x>2$
. We have that
$x>2$
. We have that
![]() $f^{\prime}(x)=2\log\!(x)-2(x-1)+(x-1)^2$
and
$f^{\prime}(x)=2\log\!(x)-2(x-1)+(x-1)^2$
and
![]() $\frac{\mathrm{d}}{\mathrm{d}x}\big(2(x-1)^4/3\big)=8(x-1)^3/3$
. By the elementary inequality
$\frac{\mathrm{d}}{\mathrm{d}x}\big(2(x-1)^4/3\big)=8(x-1)^3/3$
. By the elementary inequality
![]() $\log\!(u)\leq u-1$
for
$\log\!(u)\leq u-1$
for
![]() $u\geq1$
, we get that
$u\geq1$
, we get that
 \begin{align*} |f^{\prime}(x)|&=|2\log\!(x)-2(x-1)+(x-1)^2|\\ &=2\log\!(x)-2(x-1)+(x-1)^2\leq (x-1)^2\leq \frac{8}{3}(x-1)^3, \end{align*}
\begin{align*} |f^{\prime}(x)|&=|2\log\!(x)-2(x-1)+(x-1)^2|\\ &=2\log\!(x)-2(x-1)+(x-1)^2\leq (x-1)^2\leq \frac{8}{3}(x-1)^3, \end{align*}
where the final inequality holds because
![]() $x>2$
. Therefore, for
$x>2$
. Therefore, for
![]() $x>2$
,
$x>2$
,
![]() $2(x-1)^4/3$
grows faster than
$2(x-1)^4/3$
grows faster than
![]() $|f(x)|$
. Since
$|f(x)|$
. Since
![]() $|f(2)|<2(2-1)^4/3=2/3$
, it follows that inequality (50) holds for all
$|f(2)|<2(2-1)^4/3=2/3$
, it follows that inequality (50) holds for all
![]() $x>2$
. We have now shown that (50) is satisfied for all
$x>2$
. We have now shown that (50) is satisfied for all
![]() $x\geq0$
, as required.
$x\geq0$
, as required.
(ii) Suppose
![]() $\lambda\geq3$
. Again, without loss of generality, we may set
$\lambda\geq3$
. Again, without loss of generality, we may set
![]() $a=1$
. We therefore need to prove that, for
$a=1$
. We therefore need to prove that, for
![]() $x\geq0$
,
$x\geq0$
,
where
By a Taylor expansion of
![]() $x^{\lambda+1}$
about
$x^{\lambda+1}$
about
![]() $x=1$
we have that
$x=1$
we have that
where
![]() $\xi>0$
is between 1 and x. Now, as
$\xi>0$
is between 1 and x. Now, as
![]() $\xi$
is between 1 and x and because
$\xi$
is between 1 and x and because
![]() $\lambda\geq3$
, we have that
$\lambda\geq3$
, we have that
![]() $\xi^{\lambda-3}\leq(\mathrm{max}\{1,x\})^{\lambda-3} \leq 1+x^{\lambda-3}$
, and applying this inequality to (53) gives us (51), as required.
$\xi^{\lambda-3}\leq(\mathrm{max}\{1,x\})^{\lambda-3} \leq 1+x^{\lambda-3}$
, and applying this inequality to (53) gives us (51), as required.
(iii) Suppose now that
![]() $\lambda\in({-}1,3)\setminus\{0\}$
. Without loss of generality we set
$\lambda\in({-}1,3)\setminus\{0\}$
. Without loss of generality we set
![]() $a=1$
, and it therefore suffices to prove that, for
$a=1$
, and it therefore suffices to prove that, for
![]() $x\geq0$
,
$x\geq0$
,
We shall verify inequality (54) by treating the cases
![]() $0< x\leq 2$
and
$0< x\leq 2$
and
![]() $x\geq2$
separately (it is readily checked that the inequality holds at
$x\geq2$
separately (it is readily checked that the inequality holds at
![]() $x=0$
). For
$x=0$
). For
![]() $0<x<2$
(i.e.
$0<x<2$
(i.e.
![]() $|x-1|<1$
) we can use a Taylor expansion to write
$|x-1|<1$
) we can use a Taylor expansion to write
![]() $g_\lambda(x)=(x-1)^4 G_\lambda(x)$
, where
$g_\lambda(x)=(x-1)^4 G_\lambda(x)$
, where
and the generalised binomial coefficient is given by
![]() $\binom{a}{j}=[a(a-1)(a-2)\cdots(a-j+1)]/j!$
for
$\binom{a}{j}=[a(a-1)(a-2)\cdots(a-j+1)]/j!$
for
![]() $a>0$
and
$a>0$
and
![]() $j\in\mathbb{N}$
. We now observe that, since
$j\in\mathbb{N}$
. We now observe that, since
![]() $\lambda<3$
, the generalised binomial coefficients
$\lambda<3$
, the generalised binomial coefficients
![]() $\binom{\lambda+1}{k+4}$
are either positive for all even
$\binom{\lambda+1}{k+4}$
are either positive for all even
![]() $k\geq0$
and negative for all odd
$k\geq0$
and negative for all odd
![]() $k\geq1$
, or are negative for all even
$k\geq1$
, or are negative for all even
![]() $k\geq0$
and positive for all odd
$k\geq0$
and positive for all odd
![]() $k\geq1$
(or, exceptionally, always equal to zero if
$k\geq1$
(or, exceptionally, always equal to zero if
![]() $\lambda\in\{1,2\}$
, which is a trivial case in which
$\lambda\in\{1,2\}$
, which is a trivial case in which
![]() $g_\lambda(x)=0$
for all
$g_\lambda(x)=0$
for all
![]() $x\geq0$
). Hence, for
$x\geq0$
). Hence, for
![]() $0<x<2$
,
$0<x<2$
,
![]() $G_\lambda(x)$
is bounded above by
$G_\lambda(x)$
is bounded above by
![]() $|G_\lambda(0)|$
, and a short calculation using the expression in (52) (note that
$|G_\lambda(0)|$
, and a short calculation using the expression in (52) (note that
![]() $G_\lambda(x)=g_\lambda(x)/(x-1)^4$
) shows that
$G_\lambda(x)=g_\lambda(x)/(x-1)^4$
) shows that
![]() $G_\lambda(0)=|(\lambda-2)(\lambda-1)\lambda|/6$
. Thus, for
$G_\lambda(0)=|(\lambda-2)(\lambda-1)\lambda|/6$
. Thus, for
![]() $0\leq x<2$
, we have the bound
$0\leq x<2$
, we have the bound
Suppose now that
![]() $x\geq2$
. Recall from (53) that
$x\geq2$
. Recall from (53) that
where
![]() $\xi>0$
is between 1 and x. In fact, because we are considering the case
$\xi>0$
is between 1 and x. In fact, because we are considering the case
![]() $x\geq2$
, we know that
$x\geq2$
, we know that
![]() $\xi>1$
. Therefore, since
$\xi>1$
. Therefore, since
![]() $\lambda<3$
, we have that
$\lambda<3$
, we have that
![]() $\xi^{\lambda-3}<1$
. Therefore, for
$\xi^{\lambda-3}<1$
. Therefore, for
![]() $x\geq2$
,
$x\geq2$
,
where the second inequality follows because
![]() $\lambda\in({-}1,3)\setminus\{0\}$
. We have thus proved inequality (54), which completes the proof of the lemma.
$\lambda\in({-}1,3)\setminus\{0\}$
. We have thus proved inequality (54), which completes the proof of the lemma.
Acknowledgements
I would like to thank the referee for their helpful comments and suggestions.
Funding information
The author is supported by a Dame Kathleen Ollerenshaw Research Fellowship. Preliminary research on this project was carried out while the author was supported by EPSRC grant EP/K032402/1.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
Supplementary material
To view supplementary material for this article, please visit http://doi.org/10.1017/jpr.2022.7.