Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Grimmett, Geoffrey
1997.
Lectures on Probability Theory and Statistics.
Vol. 1665,
Issue. ,
p.
153.
Häggström, Olle
Schonmann, Roberto H.
and
Steif, Jeffrey E.
2000.
The Ising model on diluted graphs and strong amenability.
The Annals of Probability,
Vol. 28,
Issue. 3,


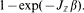 . Let
. Let 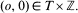 . Denote by
. Denote by 