Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-29T04:29:50.677Z Has data issue: false hasContentIssue false
  • English
  • Français

The distribution and asympotic behaviour of the negative Wiener–Hopf factor for Lévy processes with rational positive jumps

Part of: Stochastic processes Markov processes

Published online by Cambridge University Press:  11 December 2019

Ekaterina T. Kolkovska  and
Ehyter M. Martín-González
Ekaterina T. Kolkovska*
Affiliation:
Centro de Investigación en Matemáticas
Ehyter M. Martín-González*
Affiliation:
Universidad de Guanajuato
*
*Postal address: Área de Probabilidad y Estadística, Centro de Investigación en Matemáticas, A. P. 402, Guanajuato 36000, Mexico. Email address: todorova@cimat.mx
**Postal address: Departamento de Matemáticas, Universidad de Guanajuato, Mineral de Valenciana, Guanajuato 36240, Mexico.
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the distribution of the negative Wiener–Hopf factor for a class of two-sided jump Lévy processes whose positive jumps have a rational Laplace transform. The positive Wiener–Hopf factor for this class of processes was studied by Lewis and Mordecki (2008). Here we obtain a formula for the Laplace transform of the negative Wiener–Hopf factor, as well as an explicit expression for its probability density in terms of sums of convolutions of known functions. Under additional regularity conditions on the Lévy measure of the studied processes, we also provide asymptotic results as 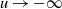$u\to-\infty$ for the distribution function F(u) of the negative Wiener–Hopf factor. We illustrate our results in some particular examples.

Keywords

Two-sided jump Lévy processWiener–Hopf factorizationnegative Wiener–Hopf factorLévy risk process

MSC classification

Primary: 60G51: Processes with independent increments; L'evy processes
Secondary: 60J25: Continuous-time Markov processes on general state spaces
Type
Research Papers
Information
Journal of Applied Probability , Volume 56 , Issue 4 , December 2019 , pp. 1086 - 1105
Copyright
© Applied Probability Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asmussen, S., Avram, F. and Pistorius, M. R. (2004). Russian and American put options under exponential phase-type Lévy models. Stoch. Process. Appl. 109, 79–111.CrossRefGoogle Scholar
Bertoin, J. (1996). Lévy Processes. Cambridge University Press.Google Scholar
Borovkov, A. (1976). Stochastic Processes in Queueing Theory. Springer, New York.CrossRefGoogle Scholar
Dickson, D. C. M. and Hipp, C. (2001). On the time to ruin for Erlang(2) risk processes. Insurance Math. Econom. 29, 333–344.CrossRefGoogle Scholar
Embrechts, P., Goldie, C. and Veraverbeke, N. (1979). Subexponentiality and infinite divisibility. Z. Wahrscheinlichkeitsth. 49, 335–347.CrossRefGoogle Scholar
Feller, W. (1971). An Introduction to Probability Theory and its Applications, Vol. 2, 2nd edn. John Wiley, New York.Google Scholar
Kolkovska, E. T. and Martn-González, E. M. (2016). Path functionals of a class of Lévy insurance risk processes. Commun. Stoch. Anal. 10, 363–387.Google Scholar
Kolkovska, E. T. and Martn-González, E. M. (2018). Asymptotic behavior of the ruin probability, the severity of ruin and the surplus prior to ruin of a two-sided jumps perturbed risk process. Progr. Probab. 73, 107–134.CrossRefGoogle Scholar
Kuznetsov, A. (2010). Wiener–Hopf factorization and distribution of extrema for a family of Lévy processes. Ann. Appl. Prob. 20, 1801–1830.CrossRefGoogle Scholar
Kuznetsov, A. (2010). Wiener–Hopf factorization for a family of Lévy processes related to theta functions. J. Appl. Prob. 47, 1023–1033.CrossRefGoogle Scholar
Kuznetsov, A. and Peng, X. (2012). On the Wiener–Hopf factorization for Lévy processes with bounded positive jumps. Stoch. Process. Appl. 122, 2610–2638.CrossRefGoogle Scholar
Kyprianou, A. (2006). Introductory Lectures on Fluctuations of Lévy Processes with Applications. Springer, Berlin.Google Scholar
Lewis, A. and Mordecki, E. (2008). Wiener–Hopf factorization for Lévy processes having positive jumps with rational transforms. J. Appl. Prob. 45, 118–134.CrossRefGoogle Scholar
Rolski, T., Schmidli, H., Schmidt, V. and Teugels, J. (1999). Stochastic Processes for Insurance and Finance. John Wiley, Chichester.CrossRefGoogle Scholar
Sato, K. (1999). Lévy Processes and Infinitely Divisible Distributions. Cambridge University Press.Google Scholar