Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ghosh, Pankaj
1974.
On generalized unimodality.
Communications in Statistics,
Vol. 3,
Issue. 6,
p.
567.
Dharmadhikari, S. W.
and
Jogdeo, Kumar
1974.
Convolutions of ?-modal distributions.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 30,
Issue. 3,
p.
203.
Wolfe, Stephen James
1975.
On the unimodality of spherically symmetric stable distribution functions.
Journal of Multivariate Analysis,
Vol. 5,
Issue. 2,
p.
236.
Dharmadhikari, S. W.
and
Jogdeo, Kumar
1976.
On characterizations of unimodality of discrete distributions.
Annals of the Institute of Statistical Mathematics,
Vol. 28,
Issue. 1,
p.
9.
Wolfe, Stephen James
1978.
On the unimodality of multivariate symmetric distribution functions of class L.
Journal of Multivariate Analysis,
Vol. 8,
Issue. 1,
p.
141.
Gupta, Somesh Das
1980.
Brunn-Minkowski inequality and its aftermath.
Journal of Multivariate Analysis,
Vol. 10,
Issue. 3,
p.
296.
Rivest, Louis-Paul
1981.
A Probabilistic Approach to the Convolution Transform.
Canadian Mathematical Bulletin,
Vol. 24,
Issue. 2,
p.
205.
Bryson, Maurice C.
and
Johnson, Mark E.
1982.
Constructing and simulating multivariate distributions using khintchine's theorem.
Journal of Statistical Computation and Simulation,
Vol. 16,
Issue. 2,
p.
129.
Bertin, Emile M. J.
and
Theodorescu, Radu
1984.
Hin?in spaces and unimodal probability measures.
Mathematische Annalen,
Vol. 266,
Issue. 3,
p.
357.
Wefelmeyer, Wolfgang
1985.
A counterexample concerning monotone unimodality.
Statistics & Probability Letters,
Vol. 3,
Issue. 2,
p.
87.
Alamatsaz, M. H.
1985.
A note on an article by Artikis.
Acta Mathematica Hungarica,
Vol. 45,
Issue. 1-2,
p.
159.
Abouammoh, A.M.
1987.
On Discrete oc–Unimodality.
Statistica Neerlandica,
Vol. 41,
Issue. 4,
p.
239.
1987.
Multivariate Statistical Simulation.
p.
211.
Steutel, F.W.
1988.
Note on discrete a‐unimodality.
Statistica Neerlandica,
Vol. 42,
Issue. 2,
p.
137.
Dharmadhikari, S. W.
and
Joag - Dev, Kumar
1989.
Upper bounds for the variances of certain random variables.
Communications in Statistics - Theory and Methods,
Vol. 18,
Issue. 9,
p.
3235.
Bertin, Emile
and
Theodorescu, Radu
1989.
On the unimodality of discrete probability measures.
Mathematische Zeitschrift,
Vol. 201,
Issue. 1,
p.
131.
Berk, Robert
and
Hwang, Jiunn T
1989.
Optimality of the least squares estimator.
Journal of Multivariate Analysis,
Vol. 30,
Issue. 2,
p.
245.
Meaux, L.M.
Seaman, J.W.
and
Boullion, T.L.
1990.
Calculation of multivariate Chebyshev-type inequalities.
Computers & Mathematics with Applications,
Vol. 20,
Issue. 12,
p.
55.
Alzaid, A.A.
and
Al–Osh, D.A.
1990.
Some results on discrete a–monotonicity.
Statistica Neerlandica,
Vol. 44,
Issue. 1,
p.
29.
Meaux, Laurie M.
and
Seanam, John W.
1990.
Probability inequalities for quadratic forms.
Communications in Statistics - Theory and Methods,
Vol. 19,
Issue. 5,
p.
1863.

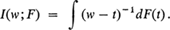
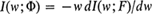 . The equivalence of Khintchine's and Isii's results is made vivid by a proof (due to L. A. Shepp) in the next section.
. The equivalence of Khintchine's and Isii's results is made vivid by a proof (due to L. A. Shepp) in the next section.