Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T17:09:22.938Z Has data issue: false hasContentIssue false
  • English
  • Français

A non-Markovian birth process with logarithmic growth

Published online by Cambridge University Press:  14 July 2016

G. R. Grimmett
G. R. Grimmett*
Affiliation:
University of Oxford
Get access Rights & Permissions [Opens in a new window]

Abstract

I show that the sum 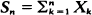of independent random variables converges in distribution when suitably normalised, so long as the Xk satisfy the following two conditions: μ(n)= E |Xn| is comparable with E |Sn| for large n, and Xk/μ(k) converges in distribution. Also I consider the associated birth process X(t) = max{n: Sn ≦ t} when each Xk is positive, and I show that there exists a continuous increasing function v(t) such that 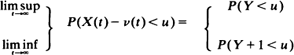for some variable Y with specified distribution, and for almost all u. The function v, satisfies v (t) = A (1 + o (t)) log t. The Markovian birth process with parameters λn = λn, where 0 < λ < 1, is an example of such a process.

Keywords

BIRTH PROCESSCONVERGENCE IN DISTRIBUTIONSUMS OF INDEPENDENT RANDOM VARIABLES
Type
Research Papers
Information
Journal of Applied Probability , Volume 12 , Issue 4 , December 1975 , pp. 673 - 683
Copyright
Copyright © Applied Probability Trust 1975 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Feller, W. (1971) An Introduction to Probability Theory and its Applications, Vol. 2, 2nd edn. Wiley, New York.Google Scholar
[2] Gnedenko, B. V. and Kolmogorov, A. N. (1954) Limit Distributions for Sums of Independent Random Variables. Addison-Wesley, Reading, Mass.Google Scholar
[3] Grimmett, G. R. (1974) Random graph theorems. Proc. 7th. Prague Conf. on Information Theory and related topics. To appear.Google Scholar
[4] Grimmett, G. R. and Mcdiarmid, C. J. H. (1975) On colouring random graphs. Math. Proc. Camb. Phil. Soc. 77, 313–324.CrossRefGoogle Scholar
[5] Jessen, B. and Wintner, A. (1935) Distribution functions and the Riemann zeta function. Trans. Amer. Math. Soc. 38, 48–88.CrossRefGoogle Scholar
[6] Levy, P. (1931) Sur les séries dont les termes sont des variables éventuelles indépendentes. Studia Mathematica 3, 119–155.CrossRefGoogle Scholar
[7] Waugh, W. A. O'N. (1974) Modes of growth of counting processes with increasing arrival rates. J. Appl. Prob. 11, 237–247.CrossRefGoogle Scholar