Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T09:22:51.911Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimization under the PMλ,τ policy of a finite dam with both continuous and jumpwise inputs

Part of: Operations research and management science Special processes

Published online by Cambridge University Press:  14 July 2016

Kyung Eun Lim ,
Jee Seon Baek  and
Eui Yong Lee
Kyung Eun Lim*
Affiliation:
Sookmyung Women's University
Jee Seon Baek*
Affiliation:
Sookmyung Women's University
Eui Yong Lee*
Affiliation:
Sookmyung Women's University
*
∗Postal address: Department of Statistics, Sookmyung Women's University, Seoul, 140-742, Korea.
∗Postal address: Department of Statistics, Sookmyung Women's University, Seoul, 140-742, Korea.
∗Postal address: Department of Statistics, Sookmyung Women's University, Seoul, 140-742, Korea.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a finite dam under the 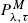policy, where the input of water is formed by a Wiener process subject to random jumps arriving according to a Poisson process. The long-run average cost per unit time is obtained after assigning costs to the changes of release rate, a reward to each unit of output, and a penalty that is a function of the level of water in the reservoir.

Keywords

Finite damPMλ,τ policyWiener processcompound Poisson processlong-run average cost

MSC classification

Primary: 60K25: Queueing theory
Secondary: 90B05: Inventory, storage, reservoirs
Type
Short Communications
Information
Journal of Applied Probability , Volume 42 , Issue 2 , June 2005 , pp. 587 - 594
Copyright
© Applied Probability Trust 2005 

References

Abdel-Hameed, M. (2000). Optimal control of a dam using P M λ,τ policies and penalty cost when the input process is a compound Poisson process with positive drift. J. Appl. Prob. 37, 408–416.Google Scholar
Asmussen, S. (1987). Applied Probability and Queues. John Wiley, Chichester.Google Scholar
Bae, J., Kim, S. and Lee, E. Y. (2003). Average cost under the P M λ,τ policy in a finite dam with compound Poisson inputs. J. Appl. Prob. 40, 519–526.Google Scholar
Cox, D. R. and Miller, H. D. (1965). The Theory of Stochastic Processes. Methuen, London.Google Scholar
Faddy, M. J. (1974). Optimal control of finite dams: discrete (2-stage) output procedure. J. Appl. Prob. 11, 111–121.Google Scholar
Lam, Y. (1985). Optimal control of a finite dam: average-cost case. J. Appl. Prob. 22, 480–484.Google Scholar
Lam, Y. and Lou, J. H. (1987). Optimal control of a finite dam. J. Appl. Prob. 24, 196–199.Google Scholar
Lee, E. Y. and Ahn, S. K. (1998). PλM-policy for a dam with input formed by a compound Poisson process. J. Appl. Prob. 35, 482–488.Google Scholar
Ross, S. M. (1983). Stochastic Processes. John Wiley, New York.Google Scholar