Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T03:32:27.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Randomized near-neighbor graphs, giant components and applications in data science

Part of: Special processes Geometric probability and stochastic geometry Graph theory

Published online by Cambridge University Press:  16 July 2020

Ariel Jaffe ,
Yuval Kluger ,
George C. Linderman ,
Gal Mishne  and
Stefan Steinerberger
Ariel Jaffe*
Affiliation:
Yale University
Yuval Kluger*
Affiliation:
Yale University
George C. Linderman*
Affiliation:
Yale University
Gal Mishne*
Affiliation:
Yale University
Stefan Steinerberger*
Affiliation:
Yale University
*
*Postal address: Program in Applied Mathematics, Yale University, New Haven, CT 06511, USA. Email address: a.jaffe@yale.edu; george.linderman@yale.edu
**Postal address: Department of Pathology and Applied Mathematics, Yale University, New Haven, CT 06511, USA. Email address: yuval.kluger@yale.edu
*Postal address: Program in Applied Mathematics, Yale University, New Haven, CT 06511, USA. Email address: a.jaffe@yale.edu; george.linderman@yale.edu
*Postal address: Program in Applied Mathematics, Yale University, New Haven, CT 06511, USA. Email address: a.jaffe@yale.edu; george.linderman@yale.edu
***Postal address: Halicioğlu Data Science Institute, UC San Diego, La Jolla, CA 92093, USA. Email address: gmishne@ucsd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

If we pick n random points uniformly in 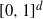$[0,1]^d$ and connect each point to its 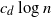$c_d \log{n}$ nearest neighbors, where 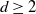$d\ge 2$ is the dimension and 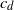$c_d$ is a constant depending on the dimension, then it is well known that the graph is connected with high probability. We prove that it suffices to connect every point to 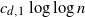$ c_{d,1} \log{\log{n}}$ points chosen randomly among its 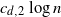$ c_{d,2} \log{n}$ nearest neighbors to ensure a giant component of size 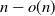$n - o(n)$ with high probability. This construction yields a much sparser random graph with 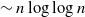$\sim n \log\log{n}$ instead of 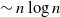$\sim n \log{n}$ edges that has comparable connectivity properties. This result has non-trivial implications for problems in data science where an affinity matrix is constructed: instead of connecting each point to its k nearest neighbors, one can often pick 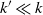$k'\ll k$ random points out of the k nearest neighbors and only connect to those without sacrificing quality of results. This approach can simplify and accelerate computation; we illustrate this with experimental results in spectral clustering of large-scale datasets.

Keywords

k-nn graphrandom graphconnectivitysparsification

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 05C40: Connectivity 05C80: Random graphs
Type
Research Papers
Information
Journal of Applied Probability , Volume 57 , Issue 2 , June 2020 , pp. 458 - 476
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balister, P. andBollobás, B. (2013). Percolation in the k-nearest neighbor graph. In Recent Results in Designs and Graphs: A Tribute to Lucia Gionfriddo (Quaderni di Matematica 28), eds Buratti, M.et al., pp. 83–100. Aracne.Google Scholar
Balister, P., Bollobás, B., Sarkar, A. andWalters, M. (2005). Connectivity of random k-nearest-neighbour graphs. Adv. Appl. Prob. 37 (1), 1–24.10.1239/aap/1113402397CrossRefGoogle Scholar
Balister, P., Bollobás, B., Sarkar, A. andWalters, M. (2009). A critical constant for the k-nearest-neighbour model. Adv. Appl. Prob. 41 (1), 1–12.10.1239/aap/1240319574CrossRefGoogle Scholar
Balister, P., Bollobás, B., Sarkar, A. andWalters, M. (2009). Highly connected random geometric graphs. Discrete Appl. Math. 157 (2), 309–320.10.1016/j.dam.2008.03.001CrossRefGoogle Scholar
Beardwood, J., Halton, J. H. andHammersley, J. M. (1959). The shortest path through many points. Proc. Cambridge Philos. Soc. 55, 299–327.10.1017/S0305004100034095CrossRefGoogle Scholar
Belkin, M. andNiyogi, P. (2003). Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 15, 1373–1396.CrossRefGoogle Scholar
Broutin, N., Devroye, L., Fraiman, N. andLugosi, G. (2014). Connectivity threshold of Bluetooth graphs. Random Struct. Algorithms 44 (1), 45–66.10.1002/rsa.20459CrossRefGoogle Scholar
Coifman, R. andLafon, S. (2006). Diffusion maps. Appl. Comput. Harmon. Anal. 21 (1), 5–30.10.1016/j.acha.2006.04.006CrossRefGoogle Scholar
Erdős, P. andRényi, A. (1959). On random graphs I. Publ. Math. Debrecen 6, 290–297.Google Scholar
Falgas-Ravry, V. andWalters, M. (2012). Sharpness in the k-nearest-neighbours random geometric graph model. Adv. Appl. Prob. 44 (3), 617–634.10.1239/aap/1346955257CrossRefGoogle Scholar
Few, L. (1955). The shortest path and the shortest road through n points. Mathematika 2, 141–144.10.1112/S0025579300000784CrossRefGoogle Scholar
Hein, M., Audibert, J.-Y. andvon Luxburg, U. (2005). From graphs to manifolds: weak and strong pointwise consistency of graph Laplacians. In Learning Theory (Lecture Notes Comput. Sci. 3559), pp. 470–485. Springer, Berlin.10.1007/11503415_32CrossRefGoogle Scholar
Hoeffding, W. (1963). Probability inequalities for sums of bounded random variables. J. Amer. Statist. Assoc. 58 (301), 13–30.CrossRefGoogle Scholar
Jones, P. W., Osipov, A. andRokhlin, V. (2011). Randomized approximate nearest neighbors algorithm. Proc. Nat. Acad. Sci. 108 (38), 15679–15686.CrossRefGoogle Scholar
Kolmogorov, A. N. andBarzdin, Y. (1993). On the realization of networks in three-dimensional space. In Selected Works of A. N. Kolmogorov (Mathematics and Its Applications (Soviet Series) 27), ed. A. N. Shiryayev, pp. 194–202. Springer, Dordrecht.Google Scholar
Kusner, M. J., Tyree, S., Weinberger, K. andAgrawal, K. (2014). Stochastic neighbor compression. In 31st International Conference on Machine Learning (Proceedings of Machine Learning Research 32), pp. 622–630. PMLR.Google Scholar
Lewis, D., Yang, Y., Rosen, T. andLi, F. (2004). RCV1: a new benchmark collection for text categorization research. J. Machine Learning Res. 5, 361–397.Google Scholar
Li, H., Linderman, G. C., Szlam, A., Stanton, K. P., Kluger, Y. andTygert, M. (2017). Algorithm 971: an implementation of a randomized algorithm for principal component analysis. ACM Trans. Math. Software 43 (3), 28.10.1145/3004053CrossRefGoogle ScholarPubMed
Linderman, G. C. andSteinerberger, S. (2019). Clustering with t-SNE, provably. SIAM J. Math Data Science 1, 313–332.10.1137/18M1216134CrossRefGoogle ScholarPubMed
Loosli, G., Canu, S. andBottou, L. (2007). Training invariant support vector machines using selective sampling. In Large Scale Kernel Machines, eds L. Bottou et al., pp. 301–320. MIT Press.Google Scholar
Maier, M., von Luxburg, U. andHein, M. (2009). Influence of graph construction on graph-based clustering measures. In Advances in Neural Information Processing Systems 21 (2008), pp. 1025–1032.Google Scholar
Maier, M., von Luxburg, U. andHein, M. (2013). How the result of graph clustering methods depends on the construction of the graph. ESAIM Prob. Statist. 17, 370–418.10.1051/ps/2012001CrossRefGoogle Scholar
Margulis, G. (1973). Explicit constructions of concentrators. Problemy Peredachi Informatsii 9 (4), 71–80. English version: Problems Inform. Transmission 10, 325–332 (1975).Google Scholar
Mauldin, R. D. (ed.) (2015). The Scottish Book: Mathematics from The Scottish Café, with Selected Problems from The New Scottish Book, 2nd edn. Birkhäuser/Springer, Cham.Google Scholar
Munkres, J. (1957). Algorithms for the assignment and transportation problems. J. Soc. Indust. Appl. Math. 5 (1), 32–38.10.1137/0105003CrossRefGoogle Scholar
Penrose, M. (2003). Random Geometric Graphs (Oxford Studies in Probability 5). Oxford University Press, Oxford.10.1093/acprof:oso/9780198506263.001.0001CrossRefGoogle Scholar
Penrose, M. andPisztora, A. (1996). Large deviations for discrete and continuous percolation. Adv. Appl. Prob. 28 (1), 29–52.CrossRefGoogle Scholar
Penrose, M. andYukich, J. (2003). Weak laws of large numbers in geometric probability. Ann. Appl. Prob. 13 (1), 277–303.CrossRefGoogle Scholar
Pinsker, M. S. (1973). On the complexity of a concentrator. In Seventh International Teletraffic Congress (Stockholm, 1973), paper # 318.Google Scholar
Rokhlin, V., Szlam, A. andTygert, M. (2009). A randomized algorithm for principal component analysis. SIAM J. Matrix Anal. Appl. 31 (3), 1100–1124.10.1137/080736417CrossRefGoogle Scholar
Shaham, U., Stanton, K., Li, H., Basri, R., Nadler, B. andKluger, Y. (2018). SpectralNet: spectral clustering using deep neural networks. In International Conference on Learning Representations, 2018.Google Scholar
Singer, A. (2006). From graph to manifold Laplacian: the convergence rate. Appl. Comput. Harmon. Anal. 21 (1), 128–134.10.1016/j.acha.2006.03.004CrossRefGoogle Scholar
Steele, J. M. (1980). Shortest paths through pseudorandom points in the d-cube. Proc. Amer. Math. Soc. 80 (1), 130–134.CrossRefGoogle Scholar
Steele, J. M. (1981). Subadditive Euclidean functionals and nonlinear growth in geometric probability. Ann. Prob. 9 (3), 365–376.CrossRefGoogle Scholar
Steele, J. M. (1997). Probability Theory and Combinatorial Optimization (CBMS-NSF Regional Conference Series in Applied Mathematics 69). SIAM, Philadelphia.Google Scholar
Steinerberger, S. (2010). A new lower bound for the geometric traveling salesman problem in terms of discrepancy. Oper. Res. Lett. 38 (4), 318–319.CrossRefGoogle Scholar
Steinerberger, S. (2015). New bounds for the traveling salesman constant. Adv. Appl. Prob. 47, 27–3610.1239/aap/1427814579CrossRefGoogle Scholar
Teng, S.-H. andYao, F. (2007). k-nearest-neighbor clustering and percolation theory. Algorithmica 49 (3), 192–211.10.1007/s00453-007-9040-7CrossRefGoogle Scholar
Walters, M. (2011). Random geometric graphs. Surveys Combin. 392, 365–402.Google Scholar
Walters, M. (2012). Small components in k-nearest neighbour graphs. Discrete Appl. Math. 160 (13–14), 2037–2047.10.1016/j.dam.2012.03.033CrossRefGoogle Scholar
van der Maaten, L. (2014). Accelerating t-SNE using tree-based algorithms. J. Machine Learning Res. 15 (1), 3221–3245.Google Scholar
van der Maaten, L. andHinton, G. (2008). Visualizing data using t-SNE. J. Machine Learning Res. 9, 2579–2605.Google Scholar
von Luxburg, U. (2007). A tutorial on spectral clustering. Statist. Comput. 17 (4), 395–416.CrossRefGoogle Scholar
Xie, J., Girshick, R. andFarhadi, A. (2016). Unsupervised deep embedding for clustering analysis. In 33rd International Conference on Machine Learning (Proceedings of Machine Learning Research 48), pp. 478–487. JMLR.Google Scholar
Xue, F. andKumar, P. R. (2004). The number of neighbors needed for connectivity of wireless networks. Wireless Networks 10, 169–181.CrossRefGoogle Scholar
Yukich, J. (1998). Probability Theory of Classical Euclidean Optimization Problems (Lecture Notes Math. 1675). Springer, Berlin.Google Scholar