Hostname: page-component-7479d7b7d-qlrfm Total loading time: 0 Render date: 2024-07-13T20:10:01.412Z Has data issue: false hasContentIssue false
  • English
  • Français

SIR epidemics driven by Feller processes

Part of: Special processes Markov processes

Published online by Cambridge University Press:  02 May 2023

Matthieu Simon Open the ORCID record for Matthieu Simon [Opens in a new window]
Matthieu Simon*
Affiliation:
Université de Mons
*
*Postal address: Département de Mathématique, Place du Parc 20, B-7000 Mons, Belgium. Email address: matthieu.simon@umons.ac.be
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a stochastic SIR (susceptible 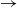$\rightarrow$ infective 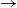$\rightarrow$ removed) model in which the infectious periods are modulated by a collection of independent and identically distributed Feller processes. Each infected individual is associated with one of these processes, the trajectories of which determine the duration of his infectious period, his contamination rate, and his type of removal (e.g. death or immunization). We use a martingale approach to derive the distribution of the final epidemic size and severity for this model and provide some general examples. Next, we focus on a single infected individual facing a given number of susceptibles, and we determine the distribution of his outcome (number of contaminations, severity, type of removal). Using a discrete-time formulation of the model, we show that this distribution also provides us with an alternative, more stable method to compute the final epidemic outcome distribution.

Keywords

SIR epidemic processesFeller processesfinal epidemic outcomemartingales

MSC classification

Primary: 60J25: Continuous-time Markov processes on general state spaces 92D30: Epidemiology
Secondary: 60K37: Processes in random environments
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 4 , December 2023 , pp. 1293 - 1316
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, H. and Britton, T. (2000). Stochastic Epidemic Models and Their Statistical Analysis (Lecture Notes Statist. 151). Springer, New York.Google Scholar
Artalejo, J., Economou, A. and Lopez-Herrero, M. (2013). Stochastic epidemic models with random environment: quasi-stationarity, extinction and final size. J. Math. Biol. 67, 799–831.Google Scholar
Ball, F. (1986). A unified approach to the distribution of total size and total area under the trajectory of infectives in epidemic models. Adv. Appl. Prob. 18, 289–310.CrossRefGoogle Scholar
Ball, F. (2019). Susceptibility sets and the final outcome of collective Reed–Frost epidemics. Methodology Comput. Appl. Prob. 21, 401–412.CrossRefGoogle Scholar
Ball, F. and Donnelly, P. (1995). Strong approximations for epidemic models. Stoch. Process. Appl. 55, 1–21.CrossRefGoogle Scholar
Ball, F., Mollison, D. and Scalia-Tomba, G. (1997). Epidemics with two levels of mixing. Ann. Appl. Prob. 7, 46–89.Google Scholar
Barbour, A. and Reinert, G. (2013). Approximating the epidemic curve. Electron. J. Prob. 18, 54.CrossRefGoogle Scholar
Black, A. and Ross, J. (2015). Computation of epidemic final size distributions. J. Theoret. Biol. 367, 159–165.CrossRefGoogle ScholarPubMed
Clancy, D. (1999). Outcomes of epidemic models with general infection and removal rate functions at certain stopping times. J. Appl. Prob. 36, 799–813.Google Scholar
Clancy, D. (2014). SIR epidemic models with general infectious period distribution. Statist. Prob. Lett. 85, 1–5.CrossRefGoogle Scholar
Daley, D. and Gani, J. (2001). Epidemic Modelling: An Introduction (Cambridge Studies in Mathematical Biology). Cambridge University Press.Google Scholar
Demiris, N. and O’Neill, P. (2006). Computation of final outcome probabilities for the generalised stochastic epidemic. Statist. Comput. 16, 309–317.CrossRefGoogle Scholar
Gani, J. and Purdue, P. (1984). Matrix-geometric methods for the general stochastic epidemic. IMA J. Math. Appl. Med. Biol. 1, 333–342.CrossRefGoogle ScholarPubMed
Gil, A., Segura, J. and Temme, N. (2001). On non-oscillating integrals for computing inhomogeneous Airy functions. Math. Comput. 70, 1183–1194.CrossRefGoogle Scholar
House, T., Ross, J. and Sirl, D. (2012). How big is an outbreak likely to be? Methods for epidemic final-size calculation. Proc. R. Soc. London A 469(2150). Available at https://doi.org/10.1098/rspa.2012.0436.CrossRefGoogle Scholar
Lefèvre, C. and Simon, M. (2020). SIR-type epidemic models as block-structured Markov processes. Methodology Comput. Appl. Prob. 22, 433–453.CrossRefGoogle Scholar
Lefèvre, C. and Utev, S. (1999). Branching approximation for the collective epidemic model. Methodology Comput. Appl. Prob. 1, 211–228.CrossRefGoogle Scholar
Neuts, M. and Li, J. (1996). An algorithmic study of S-I-R stochastic epidemic models. In Athens Conference on Applied Probability and Time Series Analysis, Vol. I, Applied Probability In Honor of J. M. Gani, ed. C. C. Heyde et al., pp. 295–306. Springer, New York.CrossRefGoogle Scholar
O’Neill, P. (1997). An epidemic model with removal-dependent infection rates. Ann. Appl. Prob. 7, 90–109.Google Scholar
Picard, P. (1980). Applications of martingale theory to some epidemic models. J. Appl. Prob. 17, 583–599.Google Scholar
Picard, P. (1984). Applications of martingale theory to some epidemic models, II. J. Appl. Prob. 21, 677–684.CrossRefGoogle Scholar
Picard, P. and Lefèvre, C. (1990). A unified analysis of the final size and severity distribution in collective Reed–Frost epidemic processes. Adv. Appl. Prob. 22, 269–294.Google Scholar
Scalia-Tomba, G. (1985). Asymptotic final-size distribution for some chain-binomial processes. Adv. Appl. Prob. 17, 477–495.CrossRefGoogle Scholar
Simon, M. (2020). SIR epidemics with stochastic infectious periods. Stoch. Process. Appl. 130, 4252–4274.CrossRefGoogle Scholar
Weiss, G. (1965). On the spread of epidemics by carriers. Biometrics 21, 481–490.CrossRefGoogle ScholarPubMed