Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-14T12:06:57.316Z Has data issue: false hasContentIssue false
  • English
  • Français

Ablation of sloping ice faces into polar seawater

Published online by Cambridge University Press:  28 January 2019

Mainak Mondal Open the ORCID record for Mainak Mondal [Opens in a new window] ,
Bishakhdatta Gayen Open the ORCID record for Bishakhdatta Gayen [Opens in a new window] ,
Ross W. Griffiths Open the ORCID record for Ross W. Griffiths [Opens in a new window]  and
Ross C. Kerr
Mainak Mondal*
Affiliation:
Research School of Earth Sciences, The Australian National University, ACT 2601, Australia
Bishakhdatta Gayen*
Affiliation:
Research School of Earth Sciences, The Australian National University, ACT 2601, Australia
Ross W. Griffiths
Affiliation:
Research School of Earth Sciences, The Australian National University, ACT 2601, Australia
Ross C. Kerr
Affiliation:
Research School of Earth Sciences, The Australian National University, ACT 2601, Australia
*
†Email addresses for correspondence: mainak.mondal@anu.edu.au, bishakhdatta.gayen@anu.edu.au
†Email addresses for correspondence: mainak.mondal@anu.edu.au, bishakhdatta.gayen@anu.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

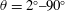The effects of the slope of an ice–seawater interface on the mechanisms and rate of ablation of the ice by natural convection are examined using turbulence-resolving simulations. Solutions are obtained for ice slopes $\unicode[STIX]{x1D703}=2^{\circ }{-}90^{\circ }$, at a fixed ambient salinity and temperature, chosen to represent common Antarctic ocean conditions. For laminar boundary layers the ablation rate decreases with height, whereas in the turbulent regime the ablation rate is found to be height independent. The simulated laminar ablation rates scale with 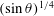$(\sin \unicode[STIX]{x1D703})^{1/4}$, whereas in the turbulent regime it follows a 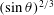$(\sin \unicode[STIX]{x1D703})^{2/3}$ scaling, both consistent with the theoretical predictions developed here. The reduction in the ablation rate with shallower slopes arises as a result of the development of stable density stratification beneath the ice face, which reduces turbulent buoyancy fluxes to the ice. The turbulent kinetic energy budget of the flow shows that, for very steep slopes, both buoyancy and shear production are drivers of turbulence, whereas for shallower slopes shear production becomes the dominant mechanism for sustaining turbulence in the convective boundary layer.

JFM classification

Convection: Buoyant boundary layers Geophysical and Geological Flows: Ice sheets Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 863 , 25 March 2019 , pp. 545 - 571
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beckmann, A. & Goosse, H. 2003 A parameterization of ice shelf–ocean interaction for climate models. Ocean Model. 5 (2), 157–170.10.1016/S1463-5003(02)00019-7Google Scholar
Budd, W. F., Jacka, T. H. & Morgan, V. I. 1980 Antarctic iceberg melt rates derived from size distributions and movement rates. Ann. Glaciol. 1, 103–112.10.3189/S0260305500017079Google Scholar
Carey, V. P. & Gebhart, B. 1982 Transport near a vertical ice surface melting in a saline water: experiments at low salinities. J. Fluid Mech. 117, 403–423.10.1017/S0022112082001682Google Scholar
Cazenave, A. & Llovel, W. 2010 Contemporary sea level rise. Ann. Rev. Mar. Sci. 2 (1), 145–173.10.1146/annurev-marine-120308-081105Google Scholar
Cooper, P. & Hunt, G. R. 2010 The ventilated filing box containing a vertically distributed source of buoyancy. J. Fluid Mech. 646, 39–58.10.1017/S0022112009992734Google Scholar
Ellison, T. H. & Turner, J. S. 1959 Turbulent entrainment in stratified flows. J. Fluid Mech. 6, 423–448.10.1017/S0022112059000738Google Scholar
Galton-Fenzi, B. K., Hunter, J. R., Coleman, R., Marsland, S. J. & Warner, R. C. 2012 Modeling the basal melting and marine ice accretion of the Amery Ice Shelf. J. Geophys. Res. 117, C09031.10.1029/2012JC008214Google Scholar
Gayen, B.2012 Turbulence and internal waves in tidal flow over topography. PhD thesis, ProQuest Dissertations and Theses, Copyright – Database copyright ProQuest LLC; ProQuest does not claim copyright in the individual underlying works; Last updated – 2016-03-11.Google Scholar
Gayen, B., Griffiths, R. W. & Hughes, G. O. 2014 Stability transitions and turbulence in horizontal convection. J. Fluid Mech. 751, 698–724.10.1017/jfm.2014.302Google Scholar
Gayen, B., Griffiths, R. W. & Kerr, R. C. 2016 Simulation of convection at a vertical ice face dissolving into saline water. J. Fluid Mech. 798, 284–298.10.1017/jfm.2016.315Google Scholar
Gayen, B. & Sarkar, S. 2011 Direct and large eddy simulations of internal tide generation at a near critical slope. J. Fluid Mech. 681, 48–79.10.1017/jfm.2011.170Google Scholar
George, W. K. & Capp, S. P. 1979 A theory for natural convection turbulent boundary layers next to heated vertical surfaces. Intl J. Heat Mass Transfer 22, 813–826.10.1016/0017-9310(79)90021-8Google Scholar
Gladish, C. V., Holland, D. M., Holland, P. R. & Price, S. F. 2012 Ice-shelf basal channels in a coupled ice/ocean model. J. Glaciol. 58, 1227–1244.10.3189/2012JoG12J003Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.10.1017/S0022112099007545Google Scholar
Holland, D. M. & Jenkins, A. J. 1999 Modeling thermodynamic ice–ocean interactions at the base of an ice shelf. J. Phys. Oceanogr. 29, 1787–1800.10.1175/1520-0485(1999)029<1787:MTIOIA>2.0.CO;22.0.CO;2>Google Scholar
Holman, J. P. 2010 Heat Transfer (McGraw-Hill Series in Mechanical Engineering), 10th edn. Science Engineering & Math.Google Scholar
Huppert, H. E. & Turner, J. S. 1978 On melting icebergs. Nature 271, 46–48.10.1038/271046a0Google Scholar
Huppert, H. E. & Turner, J. S. 1980 Ice blocks melting into a salinity gradient. J. Fluid Mech. 100, 367–384.10.1017/S0022112080001206Google Scholar
Husband, W. H. W. & Ozsahin, S. 1967 Rates of dissolution of potash ore. Canad. J. Chem. Engng 45 (4), 234–237.10.1002/cjce.5450450410Google Scholar
Jacobs, S. S., Jenkins, A., Giulivi, C. F. & Dutrieux, P. 2011 Stronger ocean circulation and increased melting under Pine Island Glacier ice shelf. Nature Geosci. 4, 519–523.10.1038/ngeo1188Google Scholar
, Jenkins, A. 1991 A one-dimensional model of ice shelf–ocean interaction. J. Geophys. Res. 96 (C11), 20671–20677.10.1029/91JC01842Google Scholar
Jenkins, A. 2011 Convection-driven melting near the grounding lines of ice shelves and tidewater glaciers. J. Phys. Oceanogr. 41, 2279–2294.10.1175/JPO-D-11-03.1Google Scholar
Jenkins, A., Dutrieux, P., Jacobs, S. S., McPhail, S. D., Perrett, J. R., Webb, A. T. & White, D. 2010 Observations beneath Pine Island Glacier in West Antarctica and implications for its retreat. Nature Geosci. 3, 468–472.10.1038/ngeo890Google Scholar
Josberger, E. G. & Martin, S. 1981 A laboratory and theoretical study of the boundary layer adjacent to a vertical melting ice wall in salt water. J. Fluid Mech. 111, 439–473.10.1017/S0022112081002450Google Scholar
Kerr, R. C. 1994 Dissolving driven by vigorous compositional convection. J. Fluid Mech. 280, 287–302.10.1017/S0022112094002934Google Scholar
Kerr, R. C. & Mcconnochie, C. D. 2015 Dissolution of a vertical solid surface by turbulent compositional convection. J. Fluid Mech. 765, 211–228.10.1017/jfm.2014.722Google Scholar
Lavergne, C., Palter, J. B., Galbraith, E. D., Bernardello, R. & Marinov, I. 2014 Cessation of deep convection in the open Southern Ocean under anthropogenic climate change. Nat. Clim. Change 4, 278–282.10.1038/nclimate2132Google Scholar
Magorrian, S. J. & Wells, A. J. 2016 Turbulent plumes from a glacier terminus melting in a stratified ocean. J. Geophys. Res. 121, 4670–4696.10.1002/2015JC011160Google Scholar
McConnochie, C. D & Kerr, R. C. 2016 The turbulent wall plume from a vertically distributed source of buoyancy. J. Fluid Mech. 787, 237–253.10.1017/jfm.2015.691Google Scholar
McConnochie, C. D. & Kerr, R. C. 2016b The effect of a salinity gradient on the dissolution of a vertical ice face. J. Fluid Mech. 791, 589–607.10.1017/jfm.2016.62Google Scholar
McConnochie, C. D. & Kerr, R. C. 2017a Enhanced ablation of a vertical ice wall due to an external freshwater plume. J. Fluid Mech. 810, 429–447.10.1017/jfm.2016.761Google Scholar
McConnochie, C. D. & Kerr, R. C. 2017b Testing a common ice-ocean parameterization with laboratory experiment. J. Geophys. Res. 122, 5905–5915.10.1002/2017JC012918Google Scholar
Morgan, V. I. & Budd, W. F. 1978 The distribution, movements and melt rates of Antarctic Iceburghs. In Iceberg Utilization: Proceedings of the First International Conference and Workshops on Iceberg Utilization for Fresh Water Production, Weather Modification and Other Applications Held at Iowa State University, Ames, Iowa, USA, October 2–6, 1977 (ed. Husseiny, A. A.), pp. 220–228. Pergamon Press.10.1016/B978-0-08-022916-4.50025-XGoogle Scholar
Morrison, A. K., Hogg, A. M. & Ward, M. L. 2011 Sensitivity of the Southern Ocean overturning circulation to surface buoyancy forcing. Geophys. Res. Lett. 38, L14602.10.1029/2011GL048031Google Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Nilson, R. H. 1985 Countercurrent convection in a double-diffusive boundary layer. J. Fluid Mech. 160, 181–210.10.1017/S0022112085003445Google Scholar
Paolo, F. S., Fricker, H. A. & Padman, L. 2016 Constructing improved decadal records of Antarctic ice shelf height change from multiple satellite radar altimeters. Remote Sens. Environ. 177, 192–205.10.1016/j.rse.2016.01.026Google Scholar
Payne, A. J., Holland, P. R., Shepherd, A. P., Rutt, I. C., Jenkins, A. & Joughin, I. 2007 Numerical modeling of ocean–ice interaction under Pine Island Bay’s ice shelf. J. Geophys. Res. 112, C10019.10.1029/2006JC003733Google Scholar
Piecuch, C. G & Ponte, R. M. 2014 Mechanisms of global-mean steric sea level change. J. Clim. 27 (2), 824–834.10.1175/JCLI-D-13-00373.1Google Scholar
Rignot, E. & Jacobs, S. S. 2002 Rapid bottom melting widespread near Antarctic ice sheet grounding lines. Science 296, 2020–2023.10.1126/science.1070942Google Scholar
Rydt, J. D. & Gudmundsson, G. H 2016 Coupled ice shelf-ocean modeling and complex grounding line retreat from a seabed ridge. J. Geophys. Res. 121, 865–880.Google Scholar
Shepherd, A., Wingham, D. & Rignot, E. 2004 Warm ocean is eroding west antarctic ice sheet. Geophys. Res. Lett. 31 (23), l23402.10.1029/2004GL021106Google Scholar
Slater, D. A., Goldberg, D. N., Nienow, P. W. & Cowton, T. R. 2016 Scalings for submarine melting at tidewater glaciers from buoyant plume theory. J. Phys. Oceanogr. 46 (6), 1839–1855.10.1175/JPO-D-15-0132.1Google Scholar
Snow, K., Hogg, A. M., Sloyan, B. M. & Downes, S. M. 2016 Sensitivity of Antarctic bottom water to change in surface buoyancy fluxes. J. Clim. 29, 313–330.10.1175/JCLI-D-15-0467.1Google Scholar
Spence, P., Griffies, S. M., England, M. H., Hogg, A. M., Saenko, O. A. & Jourdain, N. C. 2014 Rapid subsurface warming and circulation changes of Antarctic coastal waters by poleward shifting winds. Geophys. Res. Lett. 41, 7089–7096.10.1002/2014GL060613Google Scholar
Swingedouw, D., Fichefet, T., Huybrechts, P., Goosse, H., Driesschaert, E. & Loutre, M. F. 2008 Antarctic ice-sheet melting provides negative feedbacks on future climate warming. Geophys. Res. Lett. 35 (17), 17705.10.1029/2008GL034410Google Scholar
Tsuji, T. & Nagano, Y. 1988 Turbulence measurements in a natural convection boundary layer along a vertical flat plate. Intl J. Heat Mass Transfer 31 (10), 2101–2111.10.1016/0017-9310(88)90120-2Google Scholar
Turner, J. S. 1979 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Vliet, G. C. & Ross, D. C. 1975 Turbulent natural convection on upward and downward facing inclined constant heat flux surfaces. J. Heat Transfer 97 (4), 549–554.10.1115/1.3450427Google Scholar
Washburn, E. W. 1926 International Critical Tables of Numerical Data, Physics, Chemistry and Technology. The National Academies Press.Google Scholar
Weast, R. C., Astle, M. J. & Beyer, W. H. 1989 CRC Handbook of Chemistry and Physics. vol. 1990. CRC Press.Google Scholar
Wells, A. J. & Worster, M. G. 2008 A geophysical-scale model of vertical natural convection boundary layers. J. Fluid Mech. 609, 111–137.10.1017/S0022112008002346Google Scholar
Wells, A. J. & Worster, M. G. 2011 Melting and dissolving of a vertical solid surface with laminar compositional convection. J. Fluid Mech. 687, 118–140.10.1017/jfm.2011.322Google Scholar
Woods, A. W. 1992 Melting and dissolving. J. Fluid Mech. 239, 429–448.10.1017/S0022112092004476Google Scholar