Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-25T07:55:38.792Z Has data issue: false hasContentIssue false
  • English
  • Français

After transition in a soft-walled microchannel

Published online by Cambridge University Press:  07 September 2015

S. S. Srinivas  and
V. Kumaran
S. S. Srinivas
Affiliation:
Department of Chemical Engineering, Indian Institute of Science, Bangalore 560 012, India
V. Kumaran*
Affiliation:
Department of Chemical Engineering, Indian Institute of Science, Bangalore 560 012, India
*
†Email address for correspondence: kumaran@chemeng.iisc.ernet.in
Get access Rights & Permissions [Opens in a new window]

Abstract

In comparison to the flow in a rigid channel, there is a multifold reduction in the transition Reynolds number for the flow in a microchannel when one of the walls is made sufficiently soft, due to a dynamical instability induced by the fluid–wall coupling, as shown by Verma & Kumaran (J. Fluid Mech., vol. 727, 2013, pp. 407–455). The flow after transition is characterised using particle image velocimetry in the 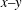$x{-}y$ plane, where $x$ is the streamwise direction and 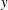$y$ is the cross-stream coordinate along the small dimension of the channel of height 0.2–0.3 mm. The flow after transition is characterised by a mean velocity profile that is flatter at the centre and steeper at the walls in comparison to that for a laminar flow. The root mean square of the streamwise fluctuating velocity shows a characteristic sharp increase away from the wall and a maximum close to the wall, as observed in turbulent flows in rigid-walled channels. However, the profile is asymmetric, with a significantly higher maximum close to the soft wall in comparison to that close to the hard wall, and the Reynolds stress is found to be non-zero at the soft wall, indicating that there is a stress exerted by fluid velocity fluctuations on the wall. The maximum of the root mean square of the velocity fluctuations and the Reynolds stress (divided by the fluid density) in the soft-walled microchannel for Reynolds numbers in the range 250–400, when scaled by suitable powers of the maximum velocity, are comparable to those in a rigid channel at Reynolds numbers in the range 5000–20 000. The near-wall velocity profile shows no evidence of a viscous sublayer for 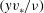$(yv_{\ast }/{\it\nu})$ as low as two, but there is a logarithmic layer for 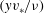$(yv_{\ast }/{\it\nu})$ up to approximately 30, where the von Karman constants are very different from those for a rigid-walled channel. Here, 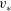$v_{\ast }$ is the friction velocity, ${\it\nu}$ is the kinematic viscosity and 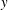$y$ is the distance from the soft surface. The surface of the soft wall in contact with the fluid is marked with dye spots to monitor the deformation and motion along the fluid–wall interface. Low-frequency oscillations in the displacement of the surface are observed after transition in both the streamwise and spanwise directions, indicating that the velocity fluctuations are dynamically coupled to motion in the solid.

JFM classification

Micro-/Nano-fluid dynamics: Microfluidics Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulent transition
Type
Papers
Information
Journal of Fluid Mechanics , Volume 780 , 10 October 2015 , pp. 649 - 686
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmed, D., Mao, X., Shi, J., Juluri, B. & Huang, T. 2009 A millisecond micromixer via single-bubble-based acoustic streaming. Lab on a Chip 9, 2738–2741.Google Scholar
del Alamo, J. C., Jimenez, J., Zandonade, P. & Moser, R. D. 2003 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
van Berkel, C., Gwyer, J. D., Deane, S., Green, N., Holloway, J., Hollisb, V. & Morgan, H. 2011 Integrated systems for rapid point of care (poc) blood cell analysis. Lab on a Chip 11, 1249–1255.Google Scholar
Bertram, C. D. 1986 Unstable equilibrium behaviour in collapsible tubes. J. Biomech. 19, 61–69.Google Scholar
Bertram, C. D., Raymond, C. J. & Pedley, T. J. 1991 Application of nonlinear dynamics concepts to the analysis of self-excited oscillations of a collapsible tube conveying a flow. J. Fluids Struct. 5, 391–426.Google Scholar
Cancelli, C. & Pedley, T. J. 1985 A separated flow model for collapsible tube oscillations. J. Fluid Mech. 157, 375–404.Google Scholar
Chokshi, P. P. & Kumaran, V. 2007 Stability of the flow of a viscoelastic fluid past a deformable surface in the low Reynolds number limit. Phys. Fluids 19, 104103.Google Scholar
Chokshi, P. P. & Kumaran, V. 2008 Weakly nonlinear analysis of viscous instability in flow past a neo-Hookean surface. Phys. Rev. E 77, 056303.CrossRefGoogle Scholar
Chokshi, P. P. & Kumaran, V. 2009 Weakly nonlinear stability analysis of a flow past a neo-Hookean solid at arbitrary Reynolds numbers. Phys. Fluids 21, 014109.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Eggert, M. D. & Kumar, S. 2004 Observations of instability, hysteresis and oscillations in low-Reynolds-number flow past polymer gels. J. Colloid Interface Sci. 274, 238–242.Google Scholar
Gaurav & Shankar, V. 2009 Stability of fluid flow through deformable neo-Hookean tubes. J. Fluid Mech. 627, 291–322.Google Scholar
Gaurav & Shankar, V. 2010 Stability of pressure-driven flow in a deformable neo-Hookean channel. J. Fluid Mech. 659, 318–350.Google Scholar
Gervais, T., El-Ali, J., Guntherb, A. & Jensen, K. F. 2006 Flow-induced deformation of shallow microfluidic channels. Lab on a Chip 6, 500–507.Google Scholar
Gkanis, V. & Kumar, S. 2005 Stability of pressure driven creeping flows in channels lined with a nonlinear elastic solid. J. Fluid Mech. 524, 357–375.Google Scholar
Han, X., van Berkel, C., Gwyer, J., Capretto, L. & Morgan, H. 2012 Microfluidic lysis of human blood for leukocyte analysis using single cell impedance cytometry. Analyt. Chem. 84, 1070–1075.Google Scholar
Hoya, S. & Jimenez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $Re_{{\it\tau}}=2003$ . Phys. Fluids 19, 011702.Google Scholar
Jensen, O. E. & Heil, M. 2003 High-frequency self-excited oscillations in a collapsible-channel flow. J. Fluid Mech. 481, 235–268.Google Scholar
Jensen, O. E. & Pedley, T. J. 1989 The existence of steady flow in a collapsed tube. J. Fluid Mech. 206, 339–374.Google Scholar
Jiang, F., Drese, K. S., Hardt, S., Kupper, M. & Schonfeld, F. 2004 Helical flows and chaotic mixing in curved micro channels. AIChE J. 50, 2297–2305.CrossRefGoogle Scholar
Kane, A. S., Hoffmann, A., Baumgartel, P., Seckler, R., Reichardt, G., Horsley, D. A., Schuler, B. & Bakajin, O. 2008 Microfluidic mixers for the investigation of rapid protein folding kinetics using synchrotron radiation circular dichroism spectroscopy. Analyt. Chem. 80, 9534–9541.Google Scholar
Krindel, P. & Silberberg, A. 1979 Flow through gel-walled tubes. J. Colloid Interface Sci. 71, 39–50.Google Scholar
Kumaran, V. 1995 Stability of the viscous flow of a fluid through a flexible tube. J. Fluid Mech. 294, 259–281.Google Scholar
Kumaran, V. 1996 Stability of an inviscid flow in a flexible tube. J. Fluid Mech. 320, 1–17.CrossRefGoogle Scholar
Kumaran, V. 1998 Stability of wall modes in a flexible tube. J. Fluid Mech. 362, 1–15.Google Scholar
Kumaran, V. 2000 Classification of instabilities in the flow past flexible surfaces. Curr. Sci. 79, 766–773.Google Scholar
Kumaran, V. 2003 Hydrodynamic stability of flow through compliant channels and tubes. In The Proceedings of IUTAM Symposium on Flow in Collapsible Tubes and Past Other Highly Compliant Boundaries (ed. Carpenter, P. W. & Pedley, T. J.). Kluwer Academic.Google Scholar
Kumaran, V., Fredrickson, G. H. & Pincus, P. 1994 Flow induced instability at the interface between a fluid and a gel at low Reynolds number. J. Phys. France II 4, 893–911.Google Scholar
Kumaran, V. & Muralikrishnan, R. 2000 Spontaneous growth of fluctuations in the viscous flow of a fluid past a soft interface. Phys. Rev. Lett. 84, 3310–3313.Google Scholar
Lahav, J., Eliezer, N. & Silberberg, A. 1973 Gel-walled cylindrical channels as models for the microcirculation: dynamics of flow. Biorheology 10, 595–604.Google Scholar
Lenzmann, F., Li, K., Kitai, A. H. & Stover, H. D. H. 1994 Thin-film micropatterning using polymer microspheres. Chem. Mater. 6, 156–159.Google Scholar
Liu, R. H., Stremler, M. A., Sharp, K. V., Olsen, M. G., Santiago, J. G., Adrian, R. J., Aref, H. & Beebe, D. J. 2000 Passive mixing in a three-dimensional serpentine microchannel. J. Microelectromech. Syst. 9, 190–197.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22 (6), 065103.CrossRefGoogle Scholar
Melling, A. 1997 Tracer particles and seeding for particle image velocimetry. Meas. Sci. Technol. 8, 1406–1416.CrossRefGoogle Scholar
de Mello, A. J. 2006 Control and detection of chemical reactions in microfluidic systems. Nature 442, 394–402.Google Scholar
Mensing, G. A., Pearce, T. M., Graham, M. D. & Beebe, D. J. 2004 An externally driven magnetic micro-stirrer. Phil. Trans. R. Soc. Lond. A 362, 1059–1068.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to $Re_{{\it\tau}}=590$ . Phys. Fluids 11, 943–945.Google Scholar
Muralikrishnan, R. & Kumaran, V. 2002 Experimental study of the instability of the viscous flow past a flexible surface. Phys. Fluids 14, 775–780.Google Scholar
Ozsun, O., Yakhot, V. & Ekinci, K. L. 2013 Non-invasive measurement of the pressure distribution in a deformable micro-channel. J. Fluid Mech. 734, R1,1–12.Google Scholar
Patel, V. C. & Head, M. R. 1969 Some observations of skin friction and velocity profiles in fully developed channel and pipe flows. J. Fluid Mech. 38, 181–201.Google Scholar
Pihler-Puzovic, D. & Pedley, T. J. 2013 Stability of high-Reynolds-number flow in a collapsible channel. J. Fluid Mech. 714, 536–561.Google Scholar
Rao, K. N., Narasimha, R. & Badri Narayanan, M. A. 1971 The ‘bursting’ phenomena in a turbulent boundary layer. J. Fluid Mech. 48, 339–352.CrossRefGoogle Scholar
Shankar, V. & Kumaran, V. 1999 Stability of non-parabolic flows in a flexible tube. J. Fluid Mech. 395, 211–236.Google Scholar
Shankar, V. & Kumaran, V. 2000 Stability of non-axisymmetric modes in a flexible tube. J. Fluid Mech. 407, 291–314.Google Scholar
Shankar, V. & Kumaran, V. 2001a Asymptotic analysis of wall modes in a flexible tube revisited. Eur. Phys. J. B 19, 607–622.Google Scholar
Shankar, V. & Kumaran, V. 2001b Weakly nonlinear stability of viscous flow past a flexible surface. J. Fluid Mech. 434, 337–354.Google Scholar
Shankar, V. & Kumaran, V. 2002 Stability of wall modes in the flow past a flexible surface. Phys. Fluids 14, 2324–2338.Google Scholar
Shapiro, A. H. 1977 Steady flow in collapsible tubes. Trans. ASME J. Biomech. Engng 99, 126–147.Google Scholar
Stroock, A. D., Dertinger, S. K. W., Ajdari, A., Mezic, I., Stone, H. A. & Whitesides, G. M. 2002 Chaotic mixer for microchannels. Nature 295, 647–651.Google Scholar
Thaokar, R. M., Shankar, V. & Kumaran, V. 2001 Effect of tangential interface motion on the viscous instability in fluid flow past flexible surfaces. Eur. Phys. J. B 23, 533–550.Google Scholar
Verma, M. K. S. & Kumaran, V. 2012 A dynamical instability due to fluid–wall coupling lowers the transition Reynolds number in the flow through a flexible tube. J. Fluid Mech. 705, 322–347.Google Scholar
Verma, M. K. S. & Kumaran, V. 2013 A multifold reduction in the transition Reynolds number, and ultra-fast mixing, in a micro-channel due to a dynamical instability induced by a soft wall. J. Fluid Mech. 727, 407–455.Google Scholar
Verma, M. K. S. & Kumaran, V. 2015 Stability of the flow in a soft tube deformed due to an applied pressure gradient. Phys. Rev. E 91, 043001.Google Scholar
Whitesides, G. 2006 The origins and the future of microfluidics. Nature 442, 368–373.Google Scholar
Yang, C., Grattoni, C. A., Muggeridge, A. H. & Zimmerman, R. M. 2000 A model for steady laminar flow through a deformable gel-coated channel. J. Colloid Interface Sci. 226, 105–111.Google Scholar