Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-27T04:53:27.206Z Has data issue: false hasContentIssue false
  • English
  • Français

An experimental study of kicked thermal turbulence

Published online by Cambridge University Press:  10 July 2008

XIAO-LI JIN  and
KE-QING XIA
XIAO-LI JIN
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
KE-QING XIA
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Get access Rights & Permissions [Opens in a new window]

Abstract

We present an experimental study of turbulent Rayleigh–Bénard convection (RBC) in which the input energy that drives the turbulent flow is in the form of periodical pulses. A surprising finding of the study is that in this ‘kicked’ thermal turbulence the heat transfer efficiency is enhanced compared to both constant and sinusoidally modulated energy inputs. For the apparatus used in the present study, an enhancement of 7% of the dimensionless Nusselt number Nu has been achieved. The enhancement is found to depend on two factors. One is the synchronization of the kicking period of energy input with the intrinsic time scale of the turbulent flow. When the repetition period of the input energy pulse equals half of the large-scale flow turnover time, a resonance or optimization of the enhancement is achieved. The other factor is the pulse shape (the inverse square of the energy input duty cycle). We find that a spiky pulse is more efficient for heat transfer than a flatter one of the same energy. It is found that in this kicked thermal turbulence there exist appropriate ranges of the kicking strength A and the kicking frequency f in which the Rayleigh number Ra grows to a saturation level and that the saturated Ra fluctuates between a lower saturation level 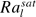and an upper saturation level 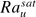. For large enough saturated Ra, power-law dependences on f and A are fou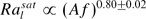nd: and 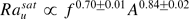. The scaling law for 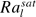is found to agree quantitatively with the prediction of a mean-field theory of kicked turbulence (Lohse, Phys. Rev. E vol. 62, 2000, p. 4946) when the latter is appropriately extended to the case of kicked thermal turbulence. It is further found that a large-scale circulatory flow (LSC) still exists in the kicked RBC, and that its Reynolds number has the same scaling with Ra as in the steadily driven case, i.e. Ref ∝ Ra0.46±0.01. The present study provides an example of achieving enhanced heat transfer in a convective system by first triggering the emission of clustered thermal plumes via an active control and then synchronizing the transport of the plume clusters with an internal time scale.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 606 , 10 July 2008 , pp. 133 - 151
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Cadot, O., Titon, J. H. & Bonn, D. 2003 Experimental observation of resonances in modulated turbulence. J. Fluid Mech. 485, 161–170.CrossRefGoogle Scholar
von der Heydt, A., Grossmann, S. & Lohse, D. 2003 a Response maxima in modulated turbulence. Phys. Rev. E 67, 046308.Google ScholarPubMed
von der Heydt, A., Grossmann, S. & Lohse, D. 2003 b Response maxima in modulated turbulence. II. Numerical simulations. Phys. Rev. E 68, 066302.Google ScholarPubMed
Hooghoudt, J.-O, Lohse, D. & Toschi, F. 2001 Decaying and kicked turbulence in a shell model. Phys. Fluids 13, 2013–2018.CrossRefGoogle Scholar
Krishnamurti, R. & Howard, L. N. 1981 Large-scale flow generation in turbulent convection. Proc. Natl Acad. Sci. USA 78, 1981–1985.CrossRefGoogle ScholarPubMed
Kuczaj, A. K., Geurts, B. J. & Lohse, D. 2006 Response maxima in time-modulated turbulence: Direct numerical simulations. Europhys. Lett. 73, 851–857.CrossRefGoogle Scholar
Lam, S., Shang, X.-D., Zhou, S.-Q. & Xia, K.-Q. 2002 Prandtl number dependence of the viscous boundary layer and the Reynolds numbers in Rayleigh-Bénard convection Phys. Rev. E 65, 066306.Google ScholarPubMed
Lohse, D. 2000 Periodically kicked turbulence Phys. Rev. E 62, 4946–4949.Google ScholarPubMed
Shang, X.-D., Qiu, X.-L., Tong, P. & Xia, K.-Q. 2003 Measured local heat transport in turbulent Rayleigh-Bénard convection Phys. Rev. Lett. 90, 074501.CrossRefGoogle ScholarPubMed
Shang, X.-D. & Xia, K.-Q. 2001 Scaling of the velocity power spectra in turbulent thermal convection. Phys. Rev. E 64, 065301(R).Google ScholarPubMed
Shraiman, B. I. & Siggia, E. D. 1990 Heat transport in high-Rayleigh-number convection Phys. Rev. A 42, 3650–3653.CrossRefGoogle ScholarPubMed
Sun, C. & Xia, K.-Q. 2007 Multi-point local temperature measurements inside the conducting plates in turbulent thermal convection. J. Fluid Mech. 570, 479–489.CrossRefGoogle Scholar
Sun, C., Xia, K.-Q. & Tong, P. 2005 Three-dimensional flow structures and dynamics of turbulent thermal convection in a cylindrical cell Phys. Rev. E 72, 026302.Google Scholar
Villermaux, E. 1995 Memory-induced low frequency oscillations in closed convection boxes. Phys. Rev. Lett. 75, 4618–4621.CrossRefGoogle ScholarPubMed
Xi, H.-D., Lam, S. & Xia, K.-Q. 2004 From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection. J. Fluid Mech. 503, 47–56.CrossRefGoogle Scholar
Xi, H.-D., Zhou, Q. & Xia, K.-Q. 2006 Azimuthal motion of the mean wind in turbulent thermal convection Phys. Rev. E 73, 056312.Google ScholarPubMed