Article contents
Asymptotic theory of resonant flow in a spheroidal cavity driven by latitudinal libration
Published online by Cambridge University Press: 06 January 2012
Abstract
We consider a homogeneous fluid of viscosity  confined within an oblate spheroidal cavity,
confined within an oblate spheroidal cavity, 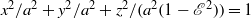 , with eccentricity
, with eccentricity 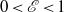 . The spheroidal container rotates rapidly with an angular velocity
. The spheroidal container rotates rapidly with an angular velocity 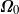 , which is fixed in an inertial frame and defines a small Ekman number
, which is fixed in an inertial frame and defines a small Ekman number 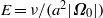 , and undergoes weak latitudinal libration with frequency
, and undergoes weak latitudinal libration with frequency 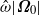 and amplitude
and amplitude 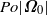 , where
, where 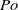 is the Poincaré number quantifying the strength of Poincaré force resulting from latitudinal libration. We investigate, via both asymptotic and numerical analysis, fluid motion in the spheroidal cavity driven by latitudinal libration. When
is the Poincaré number quantifying the strength of Poincaré force resulting from latitudinal libration. We investigate, via both asymptotic and numerical analysis, fluid motion in the spheroidal cavity driven by latitudinal libration. When 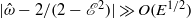 , an asymptotic solution for
, an asymptotic solution for 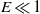 and
and 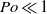 in oblate spheroidal coordinates satisfying the no-slip boundary condition is derived for a spheroidal cavity of arbitrary eccentricity without making any prior assumptions about the spatial–temporal structure of the librating flow. In this case, the librationally driven flow is non-axisymmetric with amplitude
in oblate spheroidal coordinates satisfying the no-slip boundary condition is derived for a spheroidal cavity of arbitrary eccentricity without making any prior assumptions about the spatial–temporal structure of the librating flow. In this case, the librationally driven flow is non-axisymmetric with amplitude 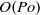 , and the role of the viscous boundary layer is primarily passive such that the flow satisfies the no-slip boundary condition. When
, and the role of the viscous boundary layer is primarily passive such that the flow satisfies the no-slip boundary condition. When 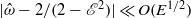 , the librationally driven flow is also non-axisymmetric but latitudinal libration resonates with a spheroidal inertial mode that is in the form of an azimuthally travelling wave in the retrograde direction. The amplitude of the flow becomes
, the librationally driven flow is also non-axisymmetric but latitudinal libration resonates with a spheroidal inertial mode that is in the form of an azimuthally travelling wave in the retrograde direction. The amplitude of the flow becomes 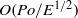 at
at 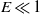 and the role of the viscous boundary layer becomes active in determining the key property of the flow. An asymptotic solution for
and the role of the viscous boundary layer becomes active in determining the key property of the flow. An asymptotic solution for 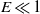 describing the librationally resonant flow is also derived for an oblate spheroidal cavity of arbitrary eccentricity. Three-dimensional direct numerical simulation in an oblate spheroidal cavity is performed to demonstrate that, in both the non-resonant and resonant cases, a satisfactory agreement is achieved between the asymptotic solution and numerical simulation at
describing the librationally resonant flow is also derived for an oblate spheroidal cavity of arbitrary eccentricity. Three-dimensional direct numerical simulation in an oblate spheroidal cavity is performed to demonstrate that, in both the non-resonant and resonant cases, a satisfactory agreement is achieved between the asymptotic solution and numerical simulation at 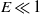 .
.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 17
- Cited by

