Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-18T07:55:49.544Z Has data issue: false hasContentIssue false
  • English
  • Français

Axial interaction of a vortex ring with a cylinder

Published online by Cambridge University Press:  09 November 2016

Debopam Das ,
Akash Manghnani ,
Mohit Bansal  and
Prafulla Sohoni
Debopam Das*
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Kanpur-208016, India
Akash Manghnani
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Kanpur-208016, India
Mohit Bansal
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Kanpur-208016, India
Prafulla Sohoni
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Kanpur, Kanpur-208016, India
*
†Email address for correspondence: das@iitk.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, axial interaction of a vortex ring with a thin circular cylinder has been studied. An apparatus to generate clean vortex rings, free of piston and stopping vortex effects, has been used. Flow visualization and particle image velocimetry (PIV) experiments are carried out to determine and compare the characteristics of free and interacting vortex rings in the Reynolds number (defined with the circulation of the free travelling vortex ring) range of 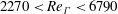$2270<Re_{\unicode[STIX]{x1D6E4}}<6790$. It is observed that due to the presence of the cylinder, there is an increase in the velocity of the vortex ring. Also, noticeable changes in the characteristic properties of vortex ring such as core circulation, core diameter and ring diameter have been observed. Changes in these parameters are explained by two changes in the flow field between the vortex ring and the cylinder due to axial interactions: (i) displacement of the streamlines and (ii) acceleration in the induced velocity field in this region. These two mutually opposing effects determine the changes in the primary vortex ring properties that take place during interaction. To justify these experimental observations quantitatively, an analytical study of the interaction under an inviscid assumption is performed. The inviscid analysis does predict the increase in velocity during the interaction, but fails to predict the values observed in the present experiments. However, when the theory is used to correct the velocity change through incorporation of the effects of an axisymmetric induced boundary layer region over the cylinder, modelled as an annular vortex sheet of varying strength, the changes in the translational velocities of the vortex rings match closely with the experimental values.

JFM classification

Vortex Flows: Vortex Flows Vortex Flows: Vortex interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 809 , 25 December 2016 , pp. 1 - 30
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allen, J. J. & Auvity, B. 2002 Interaction of a vortex ring with a piston vortex. J. Fluid Mech. 465, 353–378.CrossRefGoogle Scholar
Allen, J. J., Jouanne, Y. & Shashikanth, B. N. 2007 Vortex interaction with a moving sphere. J. Fluid Mech. 587, 337–346.CrossRefGoogle Scholar
Arakeri, J. H., Das, D., Krothapalli, A. & Lourenco, L. 2004 Vortex ring formation at the open of a shock tube: a particle image velocimetry study. Phys. Fluids 16, 1008–1019.CrossRefGoogle Scholar
Arms, R. J. & Hama, F. R. 1965 Localized induction concept on a curved vortex and motion of a elliptic vortex ring. Phys. Fluids 8, 553–559.CrossRefGoogle Scholar
Auerbach, D. 1987 Experiments on the trajectory and circulation of the starting vortex. J. Appl. Math. Phys. 183, 185–198.Google Scholar
Auerbach, D. 1991 Stirring properties of vortex rings. Phys. Fluids A 3 (5), 1351–1355.CrossRefGoogle Scholar
Barker, S. J. & Crow, S. C. 1977 The motion of two-dimensional vortex pairs in a ground effect. J. Fluid Mech. 82, 659–671.CrossRefGoogle Scholar
Blondeaux, P. & De Bernardinis, B. 1983 On the formation of vortex pairs near orifices. J. Fluid Mech. 135, 111–122.CrossRefGoogle Scholar
Boldes, U. & Ferreri, J. C. 1973 Behavior of vortex rings in the vicinity of a wall. Phys. Fluids 16, 2005–2006.CrossRefGoogle Scholar
Brasseur, J. G.1965 Evolution characteristics of vortex rings over a wide range of Reynolds numbers. AIAA Paper 65-1097.Google Scholar
Capocci, E. 1846 Su di un poco noto fenomeno vulcanico. Rend. Accad. Sci. Napoli 5, 14–18.Google Scholar
Cater, J. E., Soria, J. & Lim, T. T. 2004 The interaction of the piston vortex with a piston-generated vortex ring. J. Fluid Mech. 499, 327–343.CrossRefGoogle Scholar
Cerra, A. W. & Smith, C. R.1983 Experimental observations of vortex ring interaction with the fluid adjacent to a surface. Tech. Rep. FM-4 Bethlehem: Lehigh University.Google Scholar
Chu, C. C., Wang, C. T. & Chang, C. C. 1995 A vortex ring impinging on a solid plane surface-vortex structure and surface force. Phys. Fluids A 7, 1391–1401.CrossRefGoogle Scholar
Das, D., Bansal, M. & Manghnani, A. 2016 Generation and characteristics of classical vortex ring free of piston vortex and stopping vortex effects. J. Fluid Mech. (in press).Google Scholar
Didden, N. 1979 On the formation of vortex rings: rolling-up and production of circulation. J. Appl. Math. Phys. 30, 103–116.Google Scholar
Dwight, H. B. 1961 Tables of Integrals and Other Mathematical Data. Macmillan Publishing.Google Scholar
Dyson, F. 1893 The potential of an anchor ring – Pt. II. Phil. Trans. R. Soc. Lond. A 184, 1041–1106.Google Scholar
Fraenkel, L. E. 1972 Examples of steady vortex rings of small cross-section in an ideal fluid. J. Fluid Mech. 51, 119–135.CrossRefGoogle Scholar
Fukumoto, Y. 2010 Global time evolution of viscous vortex rings. Theor. Comput. Fluid Dyn. 24, 335–347.CrossRefGoogle Scholar
Glezer, A. 1988 The formation of vortex rings. Phys. Fluids 31, 3532–3542.CrossRefGoogle Scholar
Glezer, A. & Coles, D. 1990 An experimental study of a turbulent vortex ring. J. Fluid Mech. 221, 243–283.CrossRefGoogle Scholar
Gradshteyn, I. S. & Ryzhik, I. M. 1965 Table of Integrals, Series, and Products, 7th edn.(ed. Jeffrey, A. & Zwillinger, D.). Academic.Google Scholar
Harvey, J. & Perry, F. 1971 Flowfield produced by trailing vortices in the vicinity of the ground. AIAA J. 9 (8), 1659–1660.CrossRefGoogle Scholar
Helmholtz, H. 1858 Über integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegungen entsprechen. J. Reine Angew. Math. 55, 25–55; English translation by P. G. Tait, 1867 Phil. Mag. 33, 485–512.Google Scholar
Irdmusa, J. Z. & Garris, C. A. 1987 Influence of initial and boundary conditions on vortex ring development. AIAA J. 25 (3), 371–372.CrossRefGoogle Scholar
Kachman, N. J., Kshimoto, E. & Bernal, L. P. 1991 Vortex ring interaction with a contaminated surface at inclined incidence. In Dynamics of Bubbles and Vortices Near a Free Surface AMD-vol-119 (ed. Sahin, I., Tlyggvason, G. & Schreyer, H. L.), ASME.Google Scholar
Lamb, H. 1945 Hydrodynamics. Dover.Google Scholar
Lim, T. T. 1989 An experimental study of a vortex ring interacting with an inclined wall. Exp. Fluids 7, 453–463.CrossRefGoogle Scholar
Lim, T. T., Nickels, T. B. & Chong, M. S. 1991 A note on the cause of rebound in the head on collision of a vortex ring with a wall. Exp. Fluids 12, 41–48.CrossRefGoogle Scholar
Lim, T. T. & Nickels, T. B. 1995 Vortex rings. In Fluid Vortices (ed. Green, S. I.), Kluwer.Google Scholar
Lucey, G. K. Jr., Gher, T., Cooper, G. & Richter, R. J. 2003 Methods for using a ring vortex. U.S. Patetnt US006544347B2, Date April 8, 2003.Google Scholar
Magarvey, R. H. & MacLatchy, C. S. 1964 The disintegration of vortex rings. Can. J. Phys. 42, 684–689.CrossRefGoogle Scholar
Maxworthy, T. 1977 Some experimental studies of vortex rings. J. Fluid Mech. 81, 465–495.CrossRefGoogle Scholar
Melling, A., Durst, F. & Whitalaw, J. H. 1976 Principles and Practices of Laser-Doppler Anemometry. Academic.Google Scholar
Orlandi, P. & Verzicco, R. 1993 Vortex rings impinging on walls, axisymmetric and three dimensional simulations. J. Fluid Mech. 256, 615–646.CrossRefGoogle Scholar
Peace, A. J. & Riley, N. 1983 A viscous vortex pair in ground effect. J. Fluid Mech. 129, 409–426.CrossRefGoogle Scholar
Pullin, D. I. 1979 Vortex ring formation at tube and orifice openings. Phys. Fluids 22 (3), 401–403.CrossRefGoogle Scholar
Rice, J. A. 2006 Mathematical Statistics and Data Analysis, third edn. Duxbury Advanced.Google Scholar
Riley, N. & Stevens, D. P. 1993 A note on leapfrogging vortex rings. Fluid Dyn. Res. 11, 235–244.CrossRefGoogle Scholar
Rogers, W. B. 1858 On the formation of rotating rings by air and liquids under certain conditions of discharge. Am. J. Sci. Arts 2 26, 246–268.Google Scholar
Saffman, P. G. 1970 The velocity of viscous vortex rings. Stud. Appl. Maths 49, 371–380.CrossRefGoogle Scholar
Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Scherer, J. & Bernal, L. P.1993 HPIV study of the interaction of a vortex ring with a solid wall. AIAA 93-0413.CrossRefGoogle Scholar
Shariff, K. & Leonard, A. 1992 Vortex rings. Annu. Rev. Fluid Mech. 24, 235–279.CrossRefGoogle Scholar
Shusser, M. & Gharib, M. 2000 Energy and velocity of a forming vortex ring. Phys. Fluids 12, 618–621.CrossRefGoogle Scholar
Sohoni, P.2013 On the characteristics of vortex ring induced axisymmetric boundary layer over a circular cylinder. M. Tech. Thesis, IIT Kanpur http://172.28.64.70:8080/jspui/handle/123456789/13797.Google Scholar
Sullivan, I. S., Niemela, J. J., Hershberger, R. E., Bolster, D. & Donnelly, R. J. 2008 Dynamics of this vortex rings. J. Fluid Mech. 609, 319–347.CrossRefGoogle Scholar
Tropea, C., Yarin, A. L. & Foss, J. F. 2007 Springer Handbook of Experimental Fluid Mechanics. Springer.CrossRefGoogle Scholar
Tung, C. & Ting, L. 1967 Motion and decay of a vortex rings. Phys. Fluids 10, 901–910.CrossRefGoogle Scholar
Velasco Fuentes, O. 2014 Early observations and experiments on ring vortices. Eur. J. Mech. (B/Fluids) 43, 166–171.CrossRefGoogle Scholar
Walker, J. D. A., Smith, C. R., Cerra, A. W. & Doligalski, T. L. 1987 The impact of a vortex ring on a wall. J. Fluid Mech. 181, 99–140.CrossRefGoogle Scholar
Weigand, A. & Gharib, M. 1997 On the evolution of laminar vortex rings. Exp. Fluids 22, 447–457.CrossRefGoogle Scholar