Published online by Cambridge University Press: 03 July 2012
We present experimental results for the acoustic field of jets with Mach numbers between 0.35 and 0.6. An azimuthal ring array of six microphones, whose polar angle,  , was progressively varied, allows the decomposition of the acoustic pressure into azimuthal Fourier modes. In agreement with past observations, the sound field for low polar angles (measured with respect to the jet axis) is found to be dominated by the axisymmetric mode, particularly at the peak Strouhal number. The axisymmetric mode of the acoustic field can be clearly associated with an axially non-compact source, in the form of a wavepacket: the sound pressure level for peak frequencies is found be superdirective for all Mach numbers considered, with exponential decay as a function of
, was progressively varied, allows the decomposition of the acoustic pressure into azimuthal Fourier modes. In agreement with past observations, the sound field for low polar angles (measured with respect to the jet axis) is found to be dominated by the axisymmetric mode, particularly at the peak Strouhal number. The axisymmetric mode of the acoustic field can be clearly associated with an axially non-compact source, in the form of a wavepacket: the sound pressure level for peak frequencies is found be superdirective for all Mach numbers considered, with exponential decay as a function of 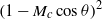 , where
, where 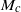 is the Mach number based on the phase velocity
is the Mach number based on the phase velocity 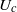 of the convected wave. While the mode
of the convected wave. While the mode 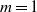 spectrum scales with Strouhal number, suggesting that its energy content is associated with turbulence scales, the axisymmetric mode scales with Helmholtz number – the ratio between source length scale and acoustic wavelength. The axisymmetric radiation has a stronger velocity dependence than the higher-order azimuthal modes, again in agreement with predictions of wavepacket models. We estimate the axial extent of the source of the axisymmetric component of the sound field to be of the order of six to eight jet diameters. This estimate is obtained in two different ways, using, respectively, the directivity shape and the velocity exponent of the sound radiation. The analysis furthermore shows that compressibility plays a significant role in the wavepacket dynamics, even at this low Mach number. Velocity fluctuations on the jet centreline are reduced as the Mach number is increased, an effect that must be accounted for in order to obtain a correct estimation of the velocity dependence of sound radiation. Finally, the higher-order azimuthal modes of the sound field are considered, and a model for the low-angle sound radiation by helical wavepackets is developed. The measured sound for azimuthal modes 1 and 2 at low Strouhal numbers is seen to correspond closely to the predicted directivity shapes.
spectrum scales with Strouhal number, suggesting that its energy content is associated with turbulence scales, the axisymmetric mode scales with Helmholtz number – the ratio between source length scale and acoustic wavelength. The axisymmetric radiation has a stronger velocity dependence than the higher-order azimuthal modes, again in agreement with predictions of wavepacket models. We estimate the axial extent of the source of the axisymmetric component of the sound field to be of the order of six to eight jet diameters. This estimate is obtained in two different ways, using, respectively, the directivity shape and the velocity exponent of the sound radiation. The analysis furthermore shows that compressibility plays a significant role in the wavepacket dynamics, even at this low Mach number. Velocity fluctuations on the jet centreline are reduced as the Mach number is increased, an effect that must be accounted for in order to obtain a correct estimation of the velocity dependence of sound radiation. Finally, the higher-order azimuthal modes of the sound field are considered, and a model for the low-angle sound radiation by helical wavepackets is developed. The measured sound for azimuthal modes 1 and 2 at low Strouhal numbers is seen to correspond closely to the predicted directivity shapes.