Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-09T09:55:50.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundary integral formulation for flows containing an interface between two porous media

Published online by Cambridge University Press:  28 February 2017

E. Ahmadi Open the ORCID record for E. Ahmadi [Opens in a new window] ,
R. Cortez  and
H. Fujioka Open the ORCID record for H. Fujioka [Opens in a new window]
E. Ahmadi*
Affiliation:
Department of Mathematics and Center for Computational Science, Tulane University, New Orleans, LA 70118, USA
R. Cortez
Affiliation:
Department of Mathematics and Center for Computational Science, Tulane University, New Orleans, LA 70118, USA
H. Fujioka
Affiliation:
Center for Computational Science, Tulane University, New Orleans, LA 70118, USA
*
†Email address for correspondence: ellie.ahmadi.2016@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

A system of boundary integral equations is derived for flows in domains composed of a porous medium of permeability 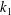$k_{1}$, surrounded by another porous medium of different permeability, 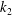$k_{2}$. The incompressible Brinkman equation is used to describe the flow in the porous media. We first apply a boundary integral representation of the Brinkman flow on each side of the dividing interface, and impose continuity of the velocity at the interface to derive the final formulation in terms of the interfacial velocity and surface forces. We discuss relations between the surface stresses based on the additional conditions imposed at the interface that depend on the porosity and permeability of the media and the structural composition of the interface. We present simulated results for test problems and different interface stress conditions. The results show significant sensitivity to the choice of the interface conditions, especially when the permeability is large. Since the Brinkman equation approaches the Stokes equation when the permeability approaches infinity, our boundary integral formulation can also be used to model the flow in sub-categories of Stokes–Stokes and Stokes–Brinkman configurations by considering infinite permeability in the Stokes fluid domain.

JFM classification

Low-Reynolds-number flows: Boundary integral methods Low-Reynolds-number flows: Low-Reynolds-number flows Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 816 , 10 April 2017 , pp. 71 - 93
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alazmi, B. & Vafai, K. 2000 Analysis of fluid flow and heat transfer interfacial conditions between a porous medium and a fluid layer. Intl J. Heat Mass Transfer 44, 1735–1749.CrossRefGoogle Scholar
Anselone, P. M. 1981 Singularity subtraction in the numerical solution of integral equations. J. Austral. Math. Soc. B 22 (4), 408–418.Google Scholar
Bear, J. & Cheng, A. 2010 Modeling Groundwater Flow and Contaminant Transport. Springer.Google Scholar
Beavers, G. S. & Joseph, D. D. 1967 Boundary conditions at a naturally permeable wall. J. Fluid Mech. 30 (1), 197–207.Google Scholar
Beavers, G. S., Sparrow, E. M. & Magnuson, R. A. 1970 Experiments on coupled parallel flows in a channel and a bounding porous medium. Trans. ASME J. Basic Engng 92D, 843–848.Google Scholar
Bhattacharyya, A. 2010 Effect of momentum transfer condition at the interface of a model of creeping flow past a spherical permeable aggregate. Eur. J. Mech. (B/Fluids) 29, 285–294.Google Scholar
Brinkman, H. 1949 A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. 1 (1), 27–34.CrossRefGoogle Scholar
Chandesris, M. & Jamet, D. 2006 Boundary condition at a planar fluid–porous interface fo a Poiseuille flow. Intl J. Heat Mass Transfer 49, 2137–2150.Google Scholar
Chen, N., Gunzburger, M. & Wang, X. 2010 Asymptotic analysis of the differences between the Stokes–Darcy system with different interface conditions and the Stokes–Brinkman system. J. Math. Anal. Appl. 368 (2), 658–676.CrossRefGoogle Scholar
Cogan, N. G., Cortez, R. & Fauci, L. 2005 Modeling physiological resistance in bacterial biofilms. Bull. Math. Biol. 67, 831–853.Google Scholar
Costerton, J. W., Stewart, P. S. & Greenberg, E. P. 1999 Bacterial biofilms: a common cause of persistent infections. Science 284 (5418), 1318–1322.CrossRefGoogle ScholarPubMed
Goyeau, B., Lhuillier, D., Gobin, D. & Velarde, M. G. 2003 Momentum transport at a fluid–porous interface. Intl J. Heat Mass Transfer 46, 4071–4081.Google Scholar
Grosan, T., Posteinicu, A. & Pop, I. 2010 Brinkman flow of a viscous fluid through a spherical porous medium embedded in another porous medium. Trans. Porous Med. 81, 89–103.Google Scholar
Higdon, J. J. L. & Kojima, M. 1981 On the calculation of Stokes’ flow past porous particles. Intl J. Multiphase Flow 7 (6), 719–727.Google Scholar
Howes, F. A. & Whitaker, S. 1985 The spatial averaging theorem revisited. Chem. Engng Sci. 40 (8), 1387–1392.CrossRefGoogle Scholar
Klapper, I. & Dockery, J. 2010 Mathematical description of microbial biofilms. SIAM Rev. 52 (2), 221–265.CrossRefGoogle Scholar
Kohr, M., Wendland, W. L. & Sekhar, G. P. R. 2009 Boundary integral equations for two-dimensional low Reynolds number flow past a porous body. Math. Meth. Appl. Sci. 32 (8), 922–962.Google Scholar
Larson, R. E. & Higdon, J. J. L. 1986 Microscopic flow near the surface of two-dimensional porous media. Part 1. Axial flow. J. Fluid Mech. 166, 449–472.CrossRefGoogle Scholar
Larson, R. E. & Higdon, J. J. L. 1987 Microscopic flow near the surface of two-dimensional porous media. Part 2. Transverse flow. J. Fluid Mech. 178, 119–136.Google Scholar
Lowe, R. J., Shavit, U., Falter, J. L., Koseff, J. R. & Monismith, S. G. 2008 Modeling flow in coral communities with and without waves: a synthesis of porous media and canopy flow approaches. Limnol. Oceanogr. 53 (6), 2668–2680.Google Scholar
Manem, J. & Rittmann, B. 1992 Removing trace level organic pollutants in a biological filter. J. Amer. Water Works 84 (4), 152–157.Google Scholar
Merrikh, A. A. & Mohamad, A. A. 2002 Non-Darcy effects in buoyancy driven flows in an enclosure filled with vertically layered porous media. Intl J. Heat Mass Transfer 45, 4305–4313.CrossRefGoogle Scholar
Neale, G. & Nader, W. 1974 Practical significance of Brinkman’s extension of Darcy’s law: coupled parallel flows within a channel and a bounding porous medium. Can. J. Chem. Engng 52, 475–478.Google Scholar
Ochoa-Tapia, J. A. 1995 Momentum transfer at the boundary between a porous medium and a homogeneous fluid – I. Theoretical development. Intl J. Heat Mass Transfer 38 (14), 2635–2646.Google Scholar
Ochoa-Tapia, J. A. & Whitaker, S. 1995 Momentum transfer at the boundary between a porous medium and a homogeneous fluid II: comparison with experiment. Intl J. Heat Mass Transfer 38 (14), 2647–2655.Google Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.Google Scholar
Pozrikidis, C. 2001 Interfacial dynamics for Stokes flow. J. Comput. Phys. 169, 250–301.Google Scholar
Richardson, S. 1971 A model for the boundary condition of a porous material. Part 2. J. Fluid Mech. 49, 327–336.Google Scholar
Saffman, P. G. 1971 On the boundary condition at the surface of porous medium. Stud. Appl. Maths 50 (2), 93–103.Google Scholar
Sahraoui, M. & Kaviany, M. 1992 Slip and no-slip velocity boundary conditions at interface of porous, plain media. Intl J. Heat Mass Transfer 35 (4), 927–943.Google Scholar
Taylor, G. I. 1971 A model for the boundary condition of a porous material. Part 1. J. Fluid Mech. 49, 319–326.CrossRefGoogle Scholar
Tlupova, S. & Cortez, R. 2009 Boundary integral solutions of coupled Stokes and Darcy flows. J. Comput. Phys. 228 (1), 158–179.Google Scholar
Valdés-Parada, F. J., Aguliar-Madera, C. G., Ochoa-Tapia, J. A. & Goyeau, B. 2013 Velocity and stress jump condition between a porous medium and a fluid. Adv. Water Resour. 62, 327–339.Google Scholar
Valdés-Parada, F. J., Alvarez-Ramirez, J., Goyeau, B. & Ochoa-Tapia, J. A. 2009 Computation of jump coefficient for momentum transfer between a porous medium and a fluid using a closed genetalized transfer equation. Trans. Porous Med. 78, 439–457.Google Scholar
Valdés-Parada, F. J., Goyeau, B. & Ochoa-Tapia, J. A. 2007 Jump momentum boundary condition at a fluid–porous dividing surface: derivation of the closure problem. Chem. Engng Sci. 62, 4025–4039.Google Scholar
Whitaker, S. 1969 Flow in porous media I: a theoretical derivation of Darcy’s law. Trans. Porous Med. 1 (1), 3–25.Google Scholar
Yano, H., Kieda, A. & Mizuno, I. 1991 The fundamental solution of Brinkman’s equation in two dimensions. Fluid Dyn. Res. 7 (3), 109–118.Google Scholar