Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
He, Xiaozhou
Funfschilling, Denis
Bodenschatz, Eberhard
and
Ahlers, Guenter
2012.
Heat transport by turbulent Rayleigh–Bénard convection forPr≃ 0.8 and 4 × 1011≲Ra≲ 2 × 1014: ultimate-state transition for aspect ratio Γ = 1.00.
New Journal of Physics,
Vol. 14,
Issue. 6,
p.
063030.
Chillà, F.
and
Schumacher, J.
2012.
New perspectives in turbulent Rayleigh-Bénard convection.
The European Physical Journal E,
Vol. 35,
Issue. 7,
Zhou, Quan
Liu, Bo-Fang
Li, Chun-Mei
and
Zhong, Bao-Chang
2012.
Aspect ratio dependence of heat transport by turbulent Rayleigh–Bénard convection in rectangular cells.
Journal of Fluid Mechanics,
Vol. 710,
Issue. ,
p.
260.
Ahlers, Guenter
He, Xiaozhou
Funfschilling, Denis
and
Bodenschatz, Eberhard
2012.
Heat transport by turbulent Rayleigh–Bénard convection forPr≃ 0.8 and 3 × 1012≲Ra≲ 1015: aspect ratio Γ = 0.50.
New Journal of Physics,
Vol. 14,
Issue. 10,
p.
103012.
Li, Ling
Shi, Nan
du Puits, Ronald
Resagk, Christian
Schumacher, Jörg
and
Thess, André
2012.
Boundary layer analysis in turbulent Rayleigh-Bénard convection in air: Experiment versus simulation.
Physical Review E,
Vol. 86,
Issue. 2,
Scheel, J. D.
Kim, E.
and
White, K. R.
2012.
Thermal and viscous boundary layers in turbulent Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 711,
Issue. ,
p.
281.
Shishkina, Olga
Horn, Susanne
and
Wagner, Sebastian
2013.
Falkner–Skan boundary layer approximation in Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 730,
Issue. ,
p.
442.
Scheel, Janet D
Emran, Mohammad S
and
Schumacher, Jörg
2013.
Resolving the fine-scale structure in turbulent Rayleigh–Bénard convection.
New Journal of Physics,
Vol. 15,
Issue. 11,
p.
113063.
Horn, Susanne
Shishkina, Olga
and
Wagner, Claus
2013.
On non-Oberbeck–Boussinesq effects in three-dimensional Rayleigh–Bénard convection in glycerol.
Journal of Fluid Mechanics,
Vol. 724,
Issue. ,
p.
175.
Zhou, Quan
and
Xia, Ke-Qing
2013.
Thermal boundary layer structure in turbulent Rayleigh–Bénard convection in a rectangular cell.
Journal of Fluid Mechanics,
Vol. 721,
Issue. ,
p.
199.
Wagner, Sebastian
and
Shishkina, Olga
2013.
Aspect-ratio dependency of Rayleigh-Bénard convection in box-shaped containers.
Physics of Fluids,
Vol. 25,
Issue. 8,
Kaczorowski, Matthias
and
Xia, Ke-Qing
2013.
Turbulent flow in the bulk of Rayleigh–Bénard convection: small-scale properties in a cubic cell.
Journal of Fluid Mechanics,
Vol. 722,
Issue. ,
p.
596.
van der Poel, Erwin P.
Stevens, Richard J. A. M.
and
Lohse, Detlef
2013.
Comparison between two- and three-dimensional Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 736,
Issue. ,
p.
177.
Horn, Susanne
and
Shishkina, Olga
2014.
Rotating non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water.
Physics of Fluids,
Vol. 26,
Issue. 5,
Wagner, Sebastian
Shishkina, Olga
and
Wagner, Claus
2014.
New Results in Numerical and Experimental Fluid Mechanics IX.
Vol. 124,
Issue. ,
p.
313.
Scheel, Janet D.
and
Schumacher, Jörg
2014.
Local boundary layer scales in turbulent Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 758,
Issue. ,
p.
344.
Wagner, Sebastian
Shishkina, Olga
and
Wagner, Claus
2014.
Turbulence and Interactions.
Vol. 125,
Issue. ,
p.
181.
Shishkina, Olga
Wagner, Sebastian
and
Horn, Susanne
2014.
Influence of the angle between the wind and the isothermal surfaces on the boundary layer structures in turbulent thermal convection.
Physical Review E,
Vol. 89,
Issue. 3,
van der Poel, Erwin P.
Ostilla-Mónico, Rodolfo
Verzicco, Roberto
Grossmann, Siegfried
and
Lohse, Detlef
2015.
Logarithmic Mean Temperature Profiles and Their Connection to Plume Emissions in Turbulent Rayleigh-Bénard Convection.
Physical Review Letters,
Vol. 115,
Issue. 15,
Wagner, S.
and
Shishkina, O.
2015.
Direct and Large-Eddy Simulation IX.
Vol. 20,
Issue. ,
p.
337.
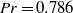 and Rayleigh numbers (
and Rayleigh numbers (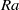 ) up to
) up to 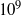 by means of highly resolved direct numerical simulations. We identify time periods in which the orientation of the large-scale circulation (LSC) is nearly constant in order to perform a statistical analysis of the LSC. The analysis is then reduced to two dimensions by considering only the plane of the LSC. Within this plane the LSC is treated as a wind with thermal and viscous boundary layers developing close to the horizontal plates. Special focus is on the spatial development of the wind magnitude and the boundary layer thicknesses along the bottom plate. A method for the local analysis of the instantaneous boundary layer thicknesses is introduced which shows a dramatically changing wind magnitude along the wind path. Furthermore a linear increase of the viscous and thermal boundary layer thickness along the wind direction is observed for all
by means of highly resolved direct numerical simulations. We identify time periods in which the orientation of the large-scale circulation (LSC) is nearly constant in order to perform a statistical analysis of the LSC. The analysis is then reduced to two dimensions by considering only the plane of the LSC. Within this plane the LSC is treated as a wind with thermal and viscous boundary layers developing close to the horizontal plates. Special focus is on the spatial development of the wind magnitude and the boundary layer thicknesses along the bottom plate. A method for the local analysis of the instantaneous boundary layer thicknesses is introduced which shows a dramatically changing wind magnitude along the wind path. Furthermore a linear increase of the viscous and thermal boundary layer thickness along the wind direction is observed for all 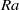 considered while their ratio is spatially constant but depends weakly on
considered while their ratio is spatially constant but depends weakly on 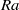 . A possible explanation is a strong spatial variation of the wind magnitude and fluctuations in the boundary layer region.
. A possible explanation is a strong spatial variation of the wind magnitude and fluctuations in the boundary layer region.