Article contents
Buoyant displacement flow of immiscible fluids in inclined pipes
Published online by Cambridge University Press: 10 July 2017
Abstract
We experimentally study the iso-viscous displacement flow of two immiscible Newtonian fluids in an inclined pipe. The fluids have the same viscosity but different densities. The displacing fluid is denser than the displaced fluid and is placed above the displaced fluid (i.e. a density-unstable configuration) in a pipe with small diameter-to-length ratio ( 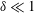 $\unicode[STIX]{x1D6FF}\ll 1$ ). In the limit considered, six dimensionless groups describe these flows: the pipe inclination angle,
$\unicode[STIX]{x1D6FF}\ll 1$ ). In the limit considered, six dimensionless groups describe these flows: the pipe inclination angle, 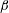 $\unicode[STIX]{x1D6FD}$ , an Atwood number,
$\unicode[STIX]{x1D6FD}$ , an Atwood number, 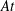 $At$ , a Reynolds number,
$At$ , a Reynolds number, 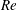 $Re$ , a densimetric Froude number,
$Re$ , a densimetric Froude number, 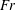 $Fr$ , a capillary number,
$Fr$ , a capillary number, 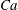 $Ca$ , and the fluids static contact angle,
$Ca$ , and the fluids static contact angle, 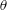 $\unicode[STIX]{x1D703}$ . Our experiments, carried out in an acrylic pipe using wetting salt-water solutions displacing non-wetting oils, cover a fairly broad range of these parameters. Completely different patterns than those of miscible flows have been observed, governed by distinct dynamics. The wetting properties of the displacing liquid and fluids immiscibility are found to significantly increase the efficiency of the displacement. During the early stage of the displacement, strong shearing is observed between the heavy and light layers, promoting Kelvin–Helmholtz instabilities. At later stages, the intensity of Kelvin–Helmholtz instabilities is reduced. However, surface-tension-driven Rayleigh-type instabilities will remain active causing droplet shedding (pearling) at displaced fluid receding contact lines. The speed of the advancing displacing front (inversely related to the displacement efficiency) is measured and characterized in dimensionless maps suggesting high values at low ranges of
$\unicode[STIX]{x1D703}$ . Our experiments, carried out in an acrylic pipe using wetting salt-water solutions displacing non-wetting oils, cover a fairly broad range of these parameters. Completely different patterns than those of miscible flows have been observed, governed by distinct dynamics. The wetting properties of the displacing liquid and fluids immiscibility are found to significantly increase the efficiency of the displacement. During the early stage of the displacement, strong shearing is observed between the heavy and light layers, promoting Kelvin–Helmholtz instabilities. At later stages, the intensity of Kelvin–Helmholtz instabilities is reduced. However, surface-tension-driven Rayleigh-type instabilities will remain active causing droplet shedding (pearling) at displaced fluid receding contact lines. The speed of the advancing displacing front (inversely related to the displacement efficiency) is measured and characterized in dimensionless maps suggesting high values at low ranges of 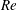 $Re$ and
$Re$ and 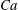 $Ca$ . Depending on the degree of flow stability and droplet formation, three major flow regimes namely viscous, transitionary and dispersed are characterized and classified in dimensionless maps. In the absence of a mean imposed velocity (exchange flow), it is found that capillary blockage may occur hindering Rayleigh–Taylor instabilities.
$Ca$ . Depending on the degree of flow stability and droplet formation, three major flow regimes namely viscous, transitionary and dispersed are characterized and classified in dimensionless maps. In the absence of a mean imposed velocity (exchange flow), it is found that capillary blockage may occur hindering Rayleigh–Taylor instabilities.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 21
- Cited by


