Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-29T19:49:48.276Z Has data issue: false hasContentIssue false
  • English
  • Français

Buoyant displacement flow of immiscible fluids in inclined pipes

Published online by Cambridge University Press:  10 July 2017

A. Hasnain ,
E. Segura  and
K. Alba Open the ORCID record for K. Alba [Opens in a new window]
A. Hasnain
Affiliation:
Department of Mechanical Engineering, University of Houston, N207 Engineering Building 1, Houston, TX 77204, USA
E. Segura
Affiliation:
Department of Engineering Technology, University of Houston, 304 Technology building 2, Houston, TX 77204, USA
K. Alba*
Affiliation:
Department of Engineering Technology, University of Houston, 304 Technology building 2, Houston, TX 77204, USA
*
†Email address for correspondence: kalba@uh.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We experimentally study the iso-viscous displacement flow of two immiscible Newtonian fluids in an inclined pipe. The fluids have the same viscosity but different densities. The displacing fluid is denser than the displaced fluid and is placed above the displaced fluid (i.e. a density-unstable configuration) in a pipe with small diameter-to-length ratio (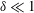$\unicode[STIX]{x1D6FF}\ll 1$). In the limit considered, six dimensionless groups describe these flows: the pipe inclination angle, 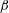$\unicode[STIX]{x1D6FD}$, an Atwood number, 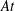$At$, a Reynolds number, 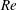$Re$, a densimetric Froude number, 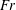$Fr$, a capillary number, 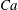$Ca$, and the fluids static contact angle, 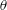$\unicode[STIX]{x1D703}$. Our experiments, carried out in an acrylic pipe using wetting salt-water solutions displacing non-wetting oils, cover a fairly broad range of these parameters. Completely different patterns than those of miscible flows have been observed, governed by distinct dynamics. The wetting properties of the displacing liquid and fluids immiscibility are found to significantly increase the efficiency of the displacement. During the early stage of the displacement, strong shearing is observed between the heavy and light layers, promoting Kelvin–Helmholtz instabilities. At later stages, the intensity of Kelvin–Helmholtz instabilities is reduced. However, surface-tension-driven Rayleigh-type instabilities will remain active causing droplet shedding (pearling) at displaced fluid receding contact lines. The speed of the advancing displacing front (inversely related to the displacement efficiency) is measured and characterized in dimensionless maps suggesting high values at low ranges of 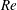$Re$ and 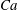$Ca$. Depending on the degree of flow stability and droplet formation, three major flow regimes namely viscous, transitionary and dispersed are characterized and classified in dimensionless maps. In the absence of a mean imposed velocity (exchange flow), it is found that capillary blockage may occur hindering Rayleigh–Taylor instabilities.

JFM classification

Instability: Instability Multiphase and Particle-laden Flows: Multiphase flow Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 824 , 10 August 2017 , pp. 661 - 687
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Al Khayyat, B., Morris, J. A., Ravi, K. & Faria, J. 1999 Successes in production-liner cementing in oil-based mud: A case study. In SPE/IADC Middle East Drill. Technol. Symposium, pp. 193–204. Society of Petroleum Engineers.Google Scholar
Alba, K., Taghavi, S. M. & Frigaard, I. A. 2012 Miscible density-stable displacement flows in inclined tube. Phys. Fluids 24, 123102.Google Scholar
Alba, K., Taghavi, S. M. & Frigaard, I. A. 2013a Miscible density-unstable displacement flows in inclined tube. Phys. Fluids 25, 067101.Google Scholar
Alba, K., Taghavi, S. M. & Frigaard, I. A. 2013b A weighted residual method for two-layer non-Newtonian channel flows: steady-state results and their stability. J. Fluid Mech. 731, 509–544.Google Scholar
Alba, K., Taghavi, S. M. & Frigaard, I. A. 2014 Miscible heavy-light displacement flows in an inclined two-dimensional channel: a numerical approach. Phys. Fluids 26 (12), 122104.Google Scholar
Amini, A., De Cesare, G. & Schleiss, A. J. 2009 Velocity profiles and interface instability in a two-phase fluid: investigations using ultrasonic velocity profiler. Exp. Fluids 46 (4), 683–692.Google Scholar
Boffetta, G. & Mazzino, A. 2017 Incompressible Rayleigh–Taylor turbulence. Annu. Rev. Fluid Mech. 49, 119–143.Google Scholar
Brunone, B. & Berni, A. 2010 Wall shear stress in transient turbulent pipe flow by local velocity measurement. ASCE J. Hydraul. Engng 136, 716–726.CrossRefGoogle Scholar
Burfoot, D., Middleton, K. E. & Holah, J. T. 2009 Removal of biofilms and stubborn soil by pressure washing. Trends Food Sci. Tech. 20, S45–S47.Google Scholar
Cantero, M. I., Lee, J. R., Balachandar, S. & Garcia, M. H. 2007 On the front velocity of gravity currents. J. Fluid Mech. 586, 1–39.Google Scholar
Cole, P. A., Asteriadou, K., Robbins, P. T., Owen, E. G., Montague, G. A. & Fryer, P. J. 2010 Comparison of cleaning of toothpaste from surfaces and pilot scale pipework. Food Bioprod. Process. 88 (4), 392–400.Google Scholar
Cook, B. P., Bertozzi, A. L. & Hosoi, A. E. 2008 Shock solutions for particle-laden thin films. SIAM J. Appl. Maths 68 (3), 760–783.Google Scholar
Debacq, M., Hulin, J. P., Salin, D., Perrin, B. & Hinch, E. J. 2003 Buoyant mixing of miscible fluids of varying viscosities in vertical tube. Phys. Fluids 15, 3846–3855.Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Dussan, E. B. 1979 On the spreading of liquids on solid surfaces: static and dynamic contact lines. Annu. Rev. Fluid Mech. 11 (1), 371–400.Google Scholar
Eres, M. H., Schwartz, L. W. & Roy, R. V. 2000 Fingering phenomena for driven coating films. Phys. Fluids 12 (6), 1278–1295.Google Scholar
Espin, L. & Kumar, S. 2017 Droplet wetting transitions on inclined substrates in the presence of external shear and substrate permeability. Phys. Rev. Fluids 2 (1), 014004.Google Scholar
Funada, T. & Joseph, D. D. 2001 Viscous potential flow analysis of Kelvin–Helmholtz instability in a channel. J. Fluid Mech. 445, 263–283.Google Scholar
Greenspan, H. P. 1978 On the motion of a small viscous droplet that wets a surface. J. Fluid Mech. 84 (01), 125–143.Google Scholar
Habchi, C., Lemenand, T., Della Valle, D. & Peerhossaini, H. 2009 Liquid/liquid dispersion in a chaotic advection flow. Intl J. Multiphase Flow 35 (6), 485–497.Google Scholar
Hallez, Y. & Magnaudet, J. 2008 Effects of channel geometry on buoyancy-driven mixing. Phys. Fluids 20, 053306.Google Scholar
Hanyang, G. U. & Liejin, G. U. O. 2008 Experimental investigation of slug development on horizontal two-phase flow. Chin. J. Chem. Engng 16 (2), 171–177.Google Scholar
Hulin, J. P., Znaien, J., Mendonca, L., Sourbier, A., Moisy, F., Salin, D. & Hinch, E. J. 2008 Buoyancy driven interpenetration of immiscible fluids of different densities in a tilted tube. In APS Div. Fluid Dynamics, vol. 1. American Physical Society.Google Scholar
Kerswell, R. R. 2011 Exchange flow of two immiscible fluids and the principle of maximum flux. J. Fluid Mech. 682, 132–159.CrossRefGoogle Scholar
Lamour, G., Hamraoui, A., Buvailo, A., Xing, Y., Keuleyan, S., Prakash, V., Eftekhari-Bafrooei, A. & Borguet, E. 2010 Contact angle measurements using a simplified experimental setup. J. Chem. Educ. 87 (12), 1403–1407.Google Scholar
Lin, P. Y. & Hanratty, T. J. 1986 Prediction of the initiation of slugs with linear stability theory. Intl J. Multiphase Flow 12 (1), 79–98.Google Scholar
Liu, X., George, E., Bo, W. & Glimm, J. 2006 Turbulent mixing with physical mass diffusion. Phys. Rev. E 73 (5), 056301.Google Scholar
Matson, G. P. & Hogg, A. J. 2012 Viscous exchange flows. Phys. Fluids 24 (2), 023102.CrossRefGoogle Scholar
Nelson, E. B. & Guillot, D. 2006 Well Cementing, 2nd edn. Schlumberger Educational Services.Google Scholar
Petitjeans, P. & Maxworthy, T. 1996 Miscible displacements in capillary tubes. Part 1. Experiments. J. Fluid Mech. 326, 37–56.Google Scholar
Podgorski, T., Flesselles, J. M. & Limat, L. 2001 Corners, cusps, and pearls in running drops. Phys. Rev. Lett. 87 (3), 036102.Google Scholar
Redapangu, P. R., Sahu, K. C. & Vanka, S. P. 2012a A study of pressure-driven displacement flow of two immiscible liquids using a multiphase lattice Boltzmann approach. Phys. Fluids 24 (10), 102110.Google Scholar
Redapangu, P. R., Sahu, K. C. & Vanka, S. P. 2013 A lattice Boltzmann simulation of three-dimensional displacement flow of two immiscible liquids in a square duct. J. Fluids Engng 135 (12), 121202.CrossRefGoogle Scholar
Redapangu, P. R., Vanka, S. P. & Sahu, K. C. 2012b Multiphase lattice Boltzmann simulations of buoyancy-induced flow of two immiscible fluids with different viscosities. Eur. J. Mech. (B/Fluids) 34, 105–114.Google Scholar
Sahu, K. C. & Vanka, S. P. 2011 A multiphase lattice Boltzmann study of buoyancy-induced mixing in a tilted channel. Comput. Fluids 50 (1), 199–215.Google Scholar
Schümann, H., Tutkun, M., Yang, Z. & Nydal, O. J. 2016 Experimental study of dispersed oil-water flow in a horizontal pipe with enhanced inlet mixing, Part 1: flow patterns, phase distributions and pressure gradients. J. Pet. Sci. Engng 145, 742–752.Google Scholar
Seon, T., Hulin, J.-P., Salin, D., Perrin, B. & Hinch, E. J. 2004 Buoyant mixing of miscible fluids in tilted tubes. Phys. Fluids 16, L103–L106.Google Scholar
Seon, T., Hulin, J.-P., Salin, D., Perrin, B. & Hinch, E. J. 2005 Buoyancy driven miscible front dynamics in tilted tubes. Phys. Fluids 17, 031702.CrossRefGoogle Scholar
Seon, T., Hulin, J.-P., Salin, D., Perrin, B. & Hinch, E. J. 2006 Laser-induced fluorescence measurements of buoyancy driven mixing in tilted tubes. Phys. Fluids 18, 041701.Google Scholar
Seon, T., Znaien, J., Salin, D., Hulin, J.-P., Hinch, E. J. & Perrin, B. 2007a Front dynamics and macroscopic diffusion in buoyant mixing in a tilted tube. Phys. Fluids 19, 125105.CrossRefGoogle Scholar
Seon, T., Znaien, J., Salin, D., Hulin, J.-P., Hinch, E. J. & Perrin, B. 2007b Transient buoyancy-driven front dynamics in nearly horizontal tubes. Phys. Fluids 19, 123603.Google Scholar
Spaid, M. A. & Homsy, G. M. 1996 Stability of Newtonian and viscoelastic dynamic contact lines. Phys. Fluids 8 (2), 460–478.Google Scholar
Stuart, J. T. 1960 On the non-linear mechanics of wave disturbances in stable and unstable parallel flows. Part 1. The basic behaviour in plane Poiseuille flow. J. Fluid Mech. 9 (03), 353–370.Google Scholar
Sundén, B. & Brebbia, C. A. 2006 Advanced Computational Methods in Heat Transfer IX, vol. 53. WIT Press.Google Scholar
Taghavi, S. M., Alba, K. & Frigaard, I. A. 2012a Buoyant miscible displacement flows at moderate viscosity ratios and low Atwood numbers in near-horizontal ducts. Chem. Engng Sci. 69, 404–418.Google Scholar
Taghavi, S. M., Alba, K., Seon, T., Wielage-Burchard, K., Martinez, D. M. & Frigaard, I. A. 2012b Miscible displacement flows in near-horizontal ducts at low Atwood number. J. Fluid Mech. 696, 175–214.Google Scholar
Taghavi, S. M., Seon, T., Martinez, D. M. & Frigaard, I. A. 2009 Buoyancy-dominated displacement flows in near-horizontal channels: the viscous limit. J. Fluid Mech. 639, 1–35.Google Scholar
Thorpe, S. A. 1969 Experiments on the instability of stratified shear flows: immiscible fluids. J. Fluid Mech. 39, 25–48.Google Scholar
Wilkinson, D. L. 1982 Motion of air cavities in long horizontal ducts. J. Fluid Mech. 118, 109–122.Google Scholar
Woods, B. D. & Hanratty, T. J. 1996 Relation of slug stability to shedding rate. Intl J. Multiphase Flow 22 (5), 809–828.Google Scholar
Zukoski, E. E. 1966 Influence of viscosity, surface tension and inclination angle on motion of long bubbles in closed tubes. J. Fluid Mech. 25, 821.CrossRefGoogle Scholar