Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-27T17:06:52.931Z Has data issue: false hasContentIssue false
  • English
  • Français

Cargo carrying with an inertial squirmer in a Newtonian fluid

Published online by Cambridge University Press:  20 March 2023

Zhenyu Ouyang Open the ORCID record for Zhenyu Ouyang [Opens in a new window] ,
Zhaowu Lin ,
Jianzhong Lin Open the ORCID record for Jianzhong Lin [Opens in a new window] ,
Zhaosheng Yu Open the ORCID record for Zhaosheng Yu [Opens in a new window]  and
Nhan Phan-Thien
Zhenyu Ouyang
Affiliation:
Zhejiang Provincial Engineering Research Center for the Safety of Pressure Vessel and Pipeline, Ningbo University, 315201 Ningbo, PR China
Zhaowu Lin
Affiliation:
Department of Mechanics, State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, 310027 Hangzhou, PR China
Jianzhong Lin*
Affiliation:
Zhejiang Provincial Engineering Research Center for the Safety of Pressure Vessel and Pipeline, Ningbo University, 315201 Ningbo, PR China
Zhaosheng Yu
Affiliation:
Department of Mechanics, State Key Laboratory of Fluid Power and Mechatronic Systems, Zhejiang University, 310027 Hangzhou, PR China
Nhan Phan-Thien
Affiliation:
Department of Mechanical Engineering, National University of Singapore, 117575 Singapore
*
†Email address for correspondence: mecjzlin@public.zju.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

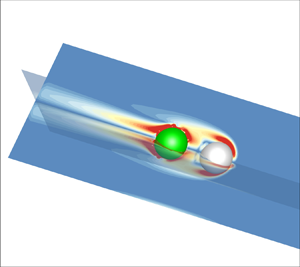
We numerically investigate the hydrodynamics of a spherical swimmer carrying a rigid cargo in a Newtonian fluid. This swimmer model, a ‘squirmer’, which is self-propelled by generating tangential surface waves, is simulated by a direct-forcing fictitious domain method (DF-FDM). We consider the effects of swimming Reynolds numbers (Re) (based on the radius and the swimming speed of the squirmers), the assembly models (related to the cargo shapes, the relative distances (ds) and positions between the squirmer and the cargo) on the assembly's locomotion. We find that the ‘pusher-cargo’ (pusher behind the cargo) model swims significantly faster than the remaining three models at the finite Re adopted in this study; the term ‘pusher’ indicates that the object is propelled from the rear, as opposed to ‘puller’, from the front. Both the ‘pusher-cargo’ and ‘cargo-pusher’ (pusher in front of the cargo) assemblies with an oblate cargo swim faster than the corresponding assemblies with a spherical or prolate cargo. In addition, the pusher-cargo model is significantly more efficient than the other models, and a larger ds yields a smaller carrying hydrodynamic efficiency η for the pusher-cargo model, but a greater η for the cargo-pusher model. We also illustrate the assembly swimming stability, finding that the ‘puller-cargo’ (puller behind the cargo) model is stable more than the ‘cargo-puller’ (puller in front of the cargo) model, and the assembly with a larger ds yields more unstable swimming.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 959 , 25 March 2023 , A25
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abraham, F.F. 1970 Functional dependence of drag coefficient of a sphere on Reynolds number. Phys. Fluids. 13 (8), 2194–2195.CrossRefGoogle Scholar
Beckett, B.S. 1986 Biology: A Modern Introduction. Oxford University Press.Google Scholar
Blake, J.R. 1971 A spherical envelope approach to ciliary propulsion. J. Fluid Mech. 46 (1), 199–208.CrossRefGoogle Scholar
Burdick, J., Laocharoensuk, R., Wheat, P.M., Posner, J.D. & Wang, J. 2008 Synthetic nanomotors in microchannel networks: directional microchip motion and controlled manipulation of cargo. J. Am. Chem. Soc. 130 (26), 8164–8165.CrossRefGoogle ScholarPubMed
Cates, M.E. & MacKintosh, F.C. 2011 Active soft matter. Soft Matt. 7 (7), 3050.CrossRefGoogle Scholar
Childress, S. 1981 Mechanics of Swimming and Flying. Cambridge University Press.CrossRefGoogle Scholar
Chisholm, N.G., Legendre, D., Lauga, E. & Khair, A.S. 2016 A squirmer across Reynolds numbers. J. Fluid Mech. 796, 233–256.CrossRefGoogle Scholar
Clopés, J., Gompper, G. & Winkler, R.G. 2020 Hydrodynamic interactions in squirmer dumbbells: active stress-induced alignment and locomotion. Soft Matt. 16 (47), 10676–10687.CrossRefGoogle ScholarPubMed
Daddi-Moussa-Ider, A., Lisicki, M. & Mathijssen, A.J. 2020 Surface rheotaxis of three-sphere microrobots with cargo. Phys. Rev. Appl. 14, 024071.CrossRefGoogle Scholar
Debnath, T. & Ghosh, P.K. 2018 Activated barrier crossing dynamics of a Janus particle carrying cargo. Phys. Chem. Chem. Phys. 20 (38), 25069–25077.CrossRefGoogle ScholarPubMed
Debnath, D., Ghosh, P.K., Li, Y., Marchesoni, F. & Li, B. 2016 Communication: cargo towing by artificial swimmers. J. Chem. Phys. 145 (19), 191103.CrossRefGoogle ScholarPubMed
Debnath, T., Ghosh, P.K., Nori, F., Li, Y., Marchesoni, F. & Li, B. 2017 Diffusion of active dimers in a Couette flow. Soft Matt. 13 (15), 2793–2799.CrossRefGoogle Scholar
Felderhof, B.U. 2014 Collinear swimmer propelling a cargo sphere at low Reynolds number. Phys. Rev. E 90 (5), 053013.Google ScholarPubMed
Fornberg, B. 1988 Steady viscous flow past a sphere at high Reynolds numbers. J. Fluid Mech. 190, 471–489.CrossRefGoogle Scholar
Gao, W., et al. 2011 Cargo-towing fuel-free magnetic nanoswimmers for targeted drug delivery. Small 8 (3), 460–467.CrossRefGoogle ScholarPubMed
Götze, I.O. & Gompper, G. 2010 Mesoscale simulations of hydrodynamic squirmer interactions. Phys. Rev. E 82 (4), 041921.CrossRefGoogle ScholarPubMed
Gutman, E. & Or, Y. 2016 Optimizing an undulating magnetic microswimmer for cargo towing. Phys. Rev. E 93 (6), 063105.CrossRefGoogle ScholarPubMed
Ishikawa, T. 2019 Stability of a dumbbell micro-swimmer. Micromachines 10 (1), 33.CrossRefGoogle ScholarPubMed
Ishikawa, T. & Hota, M. 2006 Interaction of two swimming paramecia. J. Expl Biol. 209 (22), 4452–4463.CrossRefGoogle ScholarPubMed
Ishikawa, T., Locsei, J.T. & Pedley, T.J. 2008 Development of coherent structures in concentrated suspensions of swimming model micro-organisms. J. Fluid Mech. 615, 401–431.CrossRefGoogle Scholar
Ishikawa, T. & Pedley, T.J. 2008 Coherent structures in monolayers of swimming particles. Phys. Rev. Lett. 100 (8), 088103.CrossRefGoogle ScholarPubMed
Ishikawa, T., Simmonds, M.P. & Pedley, T.J. 2006 Hydrodynamic interaction of two swimming model micro-organisms. J. Fluid Mech. 568, 119–160.CrossRefGoogle Scholar
Ishimoto, K. & Gaffney, E.A. 2013 Squirmer dynamics near a boundary. Phys. Rev. E 88 (6), 062702.CrossRefGoogle Scholar
Jan Schwarzendahl, F., & Löwen, H. 2021 Barrier-mediated predator-prey dynamics. Europhys. Lett. 134 (4), 48005.CrossRefGoogle Scholar
Jin, C., Chen, Y., Maass, C.C. & Mathijssen, A.J. 2021 Collective entrainment and confinement amplify transport by schooling microswimmers. Phys. Rev. Lett. 127 (8), 088006.CrossRefGoogle ScholarPubMed
Khair, A.S. & Chisholm, N.G. 2014 Expansions at small Reynolds numbers for the locomotion of a spherical squirmer. Phys. Fluids 26 (1), 011902.CrossRefGoogle Scholar
Kiørboe, T., Jiang, H. & Colin, S.P. 2010 Danger of zooplankton feeding: the fluid signal generated by ambush-feeding copepods. Proc. R. Soc. B: Biol. Sci. 277 (1698), 3229–3237.CrossRefGoogle ScholarPubMed
Li, G., Ostace, A. & Ardekani, A.M. 2016 Hydrodynamic interaction of swimming organisms in an inertial regime. Phys. Rev. E 94 (5), 053104.CrossRefGoogle Scholar
Lighthill, M.J. 1952 On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun. Pure Appl. Maths 5 (2), 109–118.CrossRefGoogle Scholar
Lin, Z. & Gao, T. 2019 Direct-forcing fictitious domain method for simulating non-Brownian active particles. Phys. Rev. E 100 (1), 013304.CrossRefGoogle ScholarPubMed
Magar, V., Goto, T. & Pedley, T.J. 2003 Nutrient uptake by a self-propelled steady squirmer. Q. J. Mech. Appl. Maths 56 (1), 65–91.CrossRefGoogle Scholar
Magar, V. & Pedley, T.J. 2005 Average nutrient uptake by a self-propelled unsteady squirmer. J. Fluid Mech. 539 (1), 93–112.CrossRefGoogle Scholar
More, R.V. & Ardekani, A.M. 2020 Motion of an inertial squirmer in a density stratified fluid. J. Fluid Mech. 905, A9.CrossRefGoogle Scholar
Navarro, R.M. & Pagonabarraga, I. 2010 Hydrodynamic interaction between two trapped swimming model micro-organisms. Eur. Phys. J. E 33 (1), 27–39.CrossRefGoogle Scholar
Ouyang, Z. & Lin, J. 2021 The hydrodynamics of an inertial squirmer rod. Phys. Fluids 33 (7), 073302.CrossRefGoogle Scholar
Ouyang, Z., Lin, J. & Ku, X. 2018 a Hydrodynamic properties of squirmer swimming in power-law fluid near a wall. Rheol. Acta 57 (10), 655–671.CrossRefGoogle Scholar
Ouyang, Z., Lin, J. & Ku, X. 2018 b The hydrodynamic behavior of a squirmer swimming in power-law fluid. Phys. Fluids 30 (8), 083301.CrossRefGoogle Scholar
Ouyang, Z., Lin, J. & Ku, X. 2019 Hydrodynamic interaction between a pair of swimmers in power-law fluid. Intl J. Non-Linear Mech. 108, 72–80.CrossRefGoogle Scholar
Ouyang, Z., Lin, Z., Yu, Z., Lin, J. & Phan-Thien, N. 2022 Hydrodynamics of an inertial squirmer and squirmer dumbbell in a tube. J. Fluid Mech. 939, A32.CrossRefGoogle Scholar
Ouyang, Z. & Phan-Thien, N. 2021 Inertial swimming in a channel filled with a power-law fluid. Phys. Fluids 33 (11), 113312.CrossRefGoogle Scholar
Pedley, T.J., Brumley, D.R. & Goldstein, R.E. 2016 Squirmers with swirl: a model for volvox swimming. J. Fluid Mech. 798, 165–186.CrossRefGoogle Scholar
Peng, J. & Dabiri, J.O. 2009 Transport of inertial particles by Lagrangian coherent structures: application to predator–prey interaction in jellyfish feeding. J. Fluid Mech. 623, 75–84.CrossRefGoogle Scholar
Pushkin, D.O., Shum, H. & Yeomans, J.M. 2013 Fluid transport by individual microswimmers. J. Fluid Mech. 726, 5–25.CrossRefGoogle Scholar
Raz, O. & Leshansky, A.M. 2008 Efficiency of cargo towing by a microswimmer. Phys. Rev. E 77 (5), 055305.CrossRefGoogle ScholarPubMed
Sanchez, T., Chen, D.T., DeCamp, S.J., Heymann, M. & Dogic, Z. 2012 Spontaneous motion in hierarchically assembled active matter. Nature 491 (7424), 431–434.CrossRefGoogle ScholarPubMed
Schaller, V., Weber, C., Semmrich, C., Frey, E. & Bausch, A.R. 2010 Polar patterns of driven filaments. Nature 467 (7311), 73–77.CrossRefGoogle ScholarPubMed
Solovev, A.A., Sanchez, S., Pumera, M., Mei, Y.F. & Schmidt, O.G. 2010 Magnetic control of tubular catalytic Microbots for the transport, assembly, and delivery of micro-objects. Adv. Funct. Mater. 20 (15), 2430–2435.CrossRefGoogle Scholar
Soto, R. & Golestanian, R. 2014 Self-assembly of catalytically active colloidal molecules: tailoring activity through surface chemistry. Phys. Rev. Lett. 112 (6), 068301.CrossRefGoogle ScholarPubMed
Wang, S. & Ardekani, A. 2012 Inertial squirmer. Phys. Fluids 24 (10), 101902.CrossRefGoogle Scholar
Wensink, H.H., Dunkel, J., Heidenreich, S., Drescher, K., Goldstein, R.E., Löwen, H. & Yeomans, J.M. 2012 Meso-scale turbulence in living fluids. Proc. Natl Acad. Sci. 109 (36), 14308–14313.CrossRefGoogle ScholarPubMed
Wickramarathna, L.N., Noss, C. & Lorke, A. 2014 Hydrodynamic trails produced by Daphnia: size and energetics. PLoS ONE 9 (3), e92383.CrossRefGoogle ScholarPubMed
Winkler, R.G. & Gompper, G. 2020 The physics of active polymers and filaments. J. Chem. Phys. 153 (4), 040901.CrossRefGoogle ScholarPubMed
Yu, Z. & Shao, X. 2007 A direct-forcing fictitious domain method for particulate flows. J. Comput. Phys. 227 (1), 292–314.CrossRefGoogle Scholar
Zantop, A.W. & Stark, H. 2020 Squirmer rods as elongated microswimmers: flow fields and confinement. Soft Matt. 16 (27), 6400–6412.CrossRefGoogle ScholarPubMed
Zhu, L., Do-Quang, M., Lauga, E. & Brandt, L. 2011 Locomotion by tangential deformation in a polymeric fluid. Phys. Rev. E 83 (1), 011901.CrossRefGoogle Scholar
Zöttl, A. & Stark, H. 2014 Hydrodynamics determines collective motion and phase behavior of active colloids in quasi-two-dimensional confinement. Phys. Rev. Lett. 112 (11), 118101.CrossRefGoogle ScholarPubMed