Hostname: page-component-68c7f8b79f-kpv4p Total loading time: 0 Render date: 2025-12-18T11:22:21.741Z Has data issue: false hasContentIssue false
  • English
  • Français

Coherence of unsteady wake of periodically plunging airfoil

Published online by Cambridge University Press:  14 March 2022

Burak Turhan Open the ORCID record for Burak Turhan [Opens in a new window] ,
Zhijin Wang Open the ORCID record for Zhijin Wang [Opens in a new window]  and
Ismet Gursul Open the ORCID record for Ismet Gursul [Opens in a new window]
Burak Turhan
Affiliation:
Department of Mechanical Engineering, University of Bath, Bath BA2 7AY, UK
Zhijin Wang
Affiliation:
Department of Mechanical Engineering, University of Bath, Bath BA2 7AY, UK
Ismet Gursul*
Affiliation:
Department of Mechanical Engineering, University of Bath, Bath BA2 7AY, UK
*
†Email address for correspondence: ensiag@bath.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

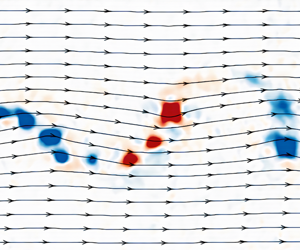
We present an experimental investigation of the flow structure in the near wake of a NACA0012 airfoil plunging sinusoidally at a chord Reynolds number of Re = 20 000 and for a wide range of reduced frequency k and Strouhal number based on peak-to-peak amplitude St. Estimated mean thrust coefficients using the mean and fluctuating velocity fields confirm the St2 dependence as well as a significant effect of the reduced frequency for k ≤ 1. Generally, time-averaged flow quantities are better correlated with St than k in the range tested (k ≤ 3.14 and St ≤ 0.24). Analysis of the streamwise flow and cross-flow in the near wake using two-point cross-correlations and proper orthogonal decomposition reveals that the unsteady characteristics are even better correlated with St than the mean flow quantities. The percentage energy of the fundamental wake modes of the streamwise flow and the flapping mode of the cross-flow increases with increasing St, but at different rates in the drag-producing and thrust-producing wakes. There are similarities to the wake synchronisation behind oscillating bodies. The spanwise-averaged cross-correlation coefficient in the measurement domain grows linearly for small St (in drag-producing wakes), and is nearly constant at a high value for larger St (in thrust-producing wakes). Results show that the Strouhal number is the most important parameter that determines the degree of two-dimensionality of the wake, and suggest that spanwise vortices are quasi-two-dimensional for St ≥ 0.05 and x/c ≤ 4. The implications for experimental gust generators using oscillating airfoils are discussed.

JFM classification

Wakes/Jets: Vortex streets Wakes/Jets: Wakes

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 938 , 10 May 2022 , A14
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Anderson, J., Streitlien, K., Barrett, D. & Triantafyllou, M. 1998 Oscillating foils of high propulsive efficiency. J. Fluid Mech. 360, 41–72.CrossRefGoogle Scholar
Bearman, P.W. 1984 Vortex shedding from oscillating bluff-bodies. Annu. Rev. Fluid Mech. 16, 195–222.CrossRefGoogle Scholar
Bendat, J. & Piersol, A. 1986 Random Data Analysis and Measurement Procedures. Hoboken.Google Scholar
Berkooz, G., Holmes, P. & Lumley, J.L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575.CrossRefGoogle Scholar
Bernal, L.P. & Roshko, A. 1986 Streamwise vortex structure in plane mixing layers. J. Fluid Mech. 170, 499–525.CrossRefGoogle Scholar
Bicknell, J. & Parker, A.G. 1972 A wind-tunnel stream oscillation apparatus. J. Aircraft 9 (6), 446–447.CrossRefGoogle Scholar
Bohl, D.G. & Koochesfahani, M.M. 2009 MTV measurements of the vortical field in the wake of an airfoil oscillating at high reduced frequency. J. Fluid Mech. 620, 63–88.CrossRefGoogle Scholar
Booth, E.R. & Yu, J.C. 1986 Two-dimensional blade-vortex flow visualization investigation. AIAA J. 24 (9), 1468–1473.CrossRefGoogle Scholar
Brion, V., Lepage, A., Amosse, Y., Soulevant, D., Senecat, P., Abart, J.C. & Paillart, P. 2015 Generation of vertical gusts in a transonic wind tunnel. Exp. Fluids 56, 145.CrossRefGoogle Scholar
Buchner, A.J., Buchmann, N., Kilany, K., Atkinson, C. & Soria, J. 2012 Stereoscopic and tomographic PIV of a pitching plate. Exp. Fluids 52, 299–314.CrossRefGoogle Scholar
Calderon, D.E., Cleaver, D.J., Gursul, I. & Wang, Z. 2014 On the absence of asymmetric wakes for periodically plunging finite wings. Phys. Fluids 26 (7), 071907.CrossRefGoogle Scholar
Charonko, J.J. & Vlachos, P.P. 2013 Estimation of uncertainty bounds for individual particle image velocimetry measurements from cross-correlation peak ratio. Meas. Sci. Technol. 24 (6), 065301.CrossRefGoogle Scholar
Chiereghin, N., Bull, S., Cleaver, D.J. & Gursul, I. 2020 Three-dimensionality of leading-edge vortices on high aspect ratio plunging wings. Phys. Rev. Fluids 5 (6), 064701.CrossRefGoogle Scholar
Chiereghin, N., Cleaver, D.J. & Gursul, I. 2019 Unsteady lift and moment of a periodically plunging airfoil. AIAA J. 57 (1), 208–222.CrossRefGoogle Scholar
Cleaver, D.J., Calderon, D.E., Wang, Z. & Gursul, I. 2013 Periodically plunging foil near a free surface. Exp. Fluids 54 (3), 1491.CrossRefGoogle Scholar
Cleaver, D.J., Wang, Z., Gursul, I. & Visbal, M.R. 2011 Lift enhancement by means of small-amplitude airfoil oscillations at low Reynolds numbers. AAIA J. 49 (9), 2018–2033.CrossRefGoogle Scholar
Cordes, U., Kampes, G., Meissner, T., Tropea, C., Peinke, J. & Holling, M. 2017 Note on the limitations of the Theodorsen and Sears functions. J. Fluid Mech. 811, R1.CrossRefGoogle Scholar
David, L., Jardin, T., Braud, P. & Farcy, A. 2012 Time-resolved scanning tomography PIV measurements around a flapping wing. Exp. Fluids 52, 857–864.CrossRefGoogle Scholar
Ekaterinaris, J. & Platzer, M. 1998 Computational prediction of airfoil dynamic stall. Prog. Aerosp. Sci. 33, 759–846.CrossRefGoogle Scholar
Fernandez, F., Cleaver, D. & Gursul, I. 2021 Unsteady aerodynamics of a wing in a novel small-amplitude transverse gust generator. Exp. Fluids 62, 9.CrossRefGoogle Scholar
Gao, A., Sherwin, S.J. & Cantwell, C.D. 2020 Three-dimensional instabilities of vortices shed from a plunging wing: computations. In Bulletin of the American Physical Society, The 73rd Annual Meeting of the APS Division of Fluid Dynamics (APS DFD 2020), 22–24 November 2020, virtual meeting.Google Scholar
Garrick, I.E. 1936 Propulsion of a flapping and oscillating airfoil. NACA Tech. Rep. 567.Google Scholar
Gilman, J. & Bennett, R.M. 1966 Wind-tunnel technique for measuring frequency-response functions for gust load analyses. J. Aircraft 3 (6), 535–540.CrossRefGoogle Scholar
Gursul, I. & Cleavers, D. 2019 Plunging oscillations of airfoils and wings: progress, opportunities, and challenges. AAIA J. 57 (9), 3648–3665.CrossRefGoogle Scholar
Hayakawa, M. & Hussain, F. 1989 Three-dimensionality of organized structures in a plane turbulent wake. J. Fluid Mech. 206, 375–404.CrossRefGoogle Scholar
Heathcote, S.F. 2006 Flexible flapping airfoil propulsion at low Reynolds numbers. PhD thesis, The University of Bath.CrossRefGoogle Scholar
Heathcote, S., Wang, Z. & Gursul, I. 2008 Effect of spanwise flexibility on flapping wing propulsion. J. Fluids Struct. 24 (2), 183–199.CrossRefGoogle Scholar
Heiland, R.W. 1992 KLTOOL: a mathematical tool for analyzing spatiotemporal data. PhD thesis, Arizona State University.Google Scholar
Jones, W.P. & Moore, J.A. 1972 Flow in the wake of a cascade of oscillating airfoils. AAIA J. 10 (12), 1600–1605.CrossRefGoogle Scholar
Karniadakis, G.E. & Triantafyllous, G.S. 1989 Frequency selection and asymptotic states in laminar wakes. J. Fluid Mech. 199, 441–469.CrossRefGoogle Scholar
Koochesfahani, M.M. 1989 Vortical patterns in the wake of an oscillating airfoil. AAIA J. 27 (9), 1200–1205.CrossRefGoogle Scholar
Lin, J.C., Vorobieff, P. & Rockwell, D. 1996 Space–time imaging of a turbulent near-wake by high-image-density particle image cinematography. Phys. Fluids 8, 555–564.CrossRefGoogle Scholar
Massaro, M. & Graham, J.M.R. 2015 The effect of three-dimensionality on the aerodynamic admittance of thin sections in free stream turbulence. J. Fluids Struct. 57, 81–90.CrossRefGoogle Scholar
Mccroskey, W.J. 1982 Unsteady airfoils. Annu. Rev. Fluid Mech. 14 (1), 285–311.CrossRefGoogle Scholar
Sears, W.R. 1941 Some aspects of non-stationary airfoil theory and its practical application. J. Aeronaut. Sci. 8 (3), 104–108.CrossRefGoogle Scholar
Shyy, W., Aono, H., Chimakurthi, S.K., Trizila, P., Kang, C.K., Cesnik, C.E.S. & Liu, H. 2010 Recent progress in flapping wing aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 46 (7), 284–327.CrossRefGoogle Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures part I: coherent structures. Q. Appl. Maths 45, 561–571.CrossRefGoogle Scholar
Smits, A.J. 2019 Undulatory and oscillatory swimming. J. Fluid Mech. 874, P1.CrossRefGoogle Scholar
Son, O., Gao, A., Gursul, I., Sherwin, S.J., Wang, Z. & Cantwell, C.D. 2022 Leading-edge vortices on plunging airfoils and wings. J. Fluid Mech. (accepted).CrossRefGoogle Scholar
Son, O., Wang, Z. & Gursul, I. 2020 Three-dimensional instabilities of vortices shed from a plunging wing: experiments. In Bulletin of the American Physical Society, 73rd Annual Meeting of the APS Division of Fluid Dynamics (APS DFD 2020), 22–24 November 2020, virtual meeting.Google Scholar
Son, O., Wang, Z. & Gursul, I. 2021 Three-dimensional instabilities of vortices on a periodically plunging wing. In AIAA Science and Technology Forum and Exposition (SciTech 2021). AIAA Paper 2021-1211.CrossRefGoogle Scholar
Squire, H.B. & Young, A.D. 1937 The calculation of the profile drag of aerofoils. Aeronautical Research Committee Reports and Memoranda 1838.Google Scholar
Sun, L., Deng, J. & Shao, X. 2018 Three-dimensional instabilities for the flow around a heaving foil. Phys. Rev. E 97 (1), 013110.CrossRefGoogle ScholarPubMed
Theodorsen, T. 1935 General theory of aerodynamic instability and the mechanism of flutter. NACA Tech. Rep. 496.Google Scholar
Triantafyllou, M.S., Triantafyllou, G.S. & Gopalkrishnan, R. 1991 Wake mechanics for thrust generation in oscillating foils. Phys. Fluids A: Fluid Dyn. 3, 2835–2837.CrossRefGoogle Scholar
Turhan, B., Wang, Z. & Gursul, I. 2020 Structure of tip vortex and wake of unsteady wings. In AIAA Science and Technology Forum and Exposition (SciTech 2020). AIAA Paper 2020-0349.CrossRefGoogle Scholar
Visbal, M.R. 2009 High-fidelity simulation of transitional flows past a plunging airfoil. AIAA J. 47 (11), 2685–2697.CrossRefGoogle Scholar
Von Karman, T.H. & Sears, W.R. 1938 Airfoil theory for non-uniform motion. J. Aeronaut. Sci. 5 (10), 379–390.CrossRefGoogle Scholar
Wei, N.J., Kissing, J. & Tropea, C. 2019 a Generation of periodic gusts with a pitching and plunging airfoil. Exp. Fluids 60 (11), 166.CrossRefGoogle Scholar
Wei, N.J., Kissing, J., Wester, T.T.B., Wegt, S., Schiffmann, K., Jakirlic, S., Holling, M., Peinke, J. & Tropea, C. 2019 b Insights into the periodic gust response of airfoils. J. Fluid Mech. 876, 237–263.CrossRefGoogle Scholar
Wei, T. & Smith, C.R. 1986 Secondary vortices in the wake of circular cylinders. J. Fluid Mech. 169, 513–533.CrossRefGoogle Scholar
Wilder, M.C. & Telionis, D.P. 1998 Parallel blade-vortex interaction. J. Fluids Struct. 12, 801–838.CrossRefGoogle Scholar
Williamson, C.H.K. 1996 Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.CrossRefGoogle Scholar
Wu, Z.L., Bangga, G., Lutz, T., Kampers, G. & Holling, M. 2020 Insights into airfoil response to sinusoidal gusty inflow by oscillating vanes. Phys. Fluids 32 (12), 125107.CrossRefGoogle Scholar
Young, J. & Lai, J.C.S. 2007 Vortex lock-in phenomenon in the wake of a plunging airfoil. AAIA J. 45 (2), 485–490.CrossRefGoogle Scholar
Zhang, Z., Wang, Z. & Gursul, I. 2022 Aerodynamics of a wing in turbulent wakes. J. Fluid Mech. (accepted).CrossRefGoogle Scholar