Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T15:45:40.991Z Has data issue: false hasContentIssue false
  • English
  • Français

Control of radial miscible viscous fingering

Published online by Cambridge University Press:  09 December 2019

Vandita Sharma Open the ORCID record for Vandita Sharma [Opens in a new window] ,
Sada Nand ,
Satyajit Pramanik Open the ORCID record for Satyajit Pramanik [Opens in a new window] ,
Ching-Yao Chen Open the ORCID record for Ching-Yao Chen [Opens in a new window]  and
Manoranjan Mishra Open the ORCID record for Manoranjan Mishra [Opens in a new window]
Vandita Sharma
Affiliation:
Department of Mathematics, Indian Institute of Technology Ropar, 140001Rupnagar, India
Sada Nand
Affiliation:
Department of Mathematics, Indian Institute of Technology Ropar, 140001Rupnagar, India
Satyajit Pramanik
Affiliation:
NORDITA, Royal Institute of Technology and Stockholm University, SE 106 91Stockholm, Sweden
Ching-Yao Chen*
Affiliation:
Department of Mechanical Engineering, National Chiao Tung University, Hsinchu, Taiwan, 30010Republic of China
Manoranjan Mishra*
Affiliation:
Department of Mathematics, Indian Institute of Technology Ropar, 140001Rupnagar, India
*
†Email addresses for correspondence: chingyao@mail.nctu.edu.tw, manoranjan@iitrpr.ac.in
†Email addresses for correspondence: chingyao@mail.nctu.edu.tw, manoranjan@iitrpr.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

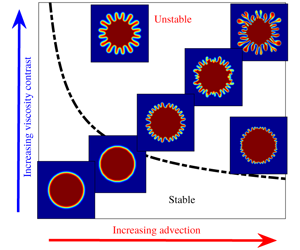
We investigate the stability of radial viscous fingering (VF) in miscible fluids. We show that the instability is determined by an interplay between advection and diffusion during the initial stages of flow. Using linear stability analysis and nonlinear simulations, we demonstrate that this competition is a function of the radius $r_{0}$ of the circular region initially occupied by the less-viscous fluid in the porous medium. For each $r_{0}$, we further determine the stability in terms of Péclet number ($Pe$) and log-mobility ratio ($M$). The $Pe{-}M$ parameter space is divided into stable and unstable zones: the boundary between the two zones is well approximated by $M_{c}=\unicode[STIX]{x1D6FC}(r_{0})Pe_{c}^{-0.55}$. In the unstable zone, the instability is reduced with an increase in $r_{0}$. Thus, a natural control measure for miscible radial VF in terms of $r_{0}$ is established. Finally, the results are validated by performing experiments that provide good qualitative agreement with our numerical study. Implications for observations in oil recovery and other fingering instabilities are discussed.

JFM classification

Convection: Convection in porous media Low-Reynolds-number flows: Hele-Shaw flows Interfacial Flows (free surface): Fingering instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A16
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amooie, M. A., Soltanian, M. R. & Moortgat, J. 2017 Hydrothermodynamic mixing of fluids across phases in porous media. Geophys. Res. Lett. 44 (8), 3624–3634.CrossRefGoogle Scholar
Ball, T. V. & Huppert, H. E. 2019 Similarity solutions and viscous gravity current adjustment times. J. Fluid Mech. 874, 285–298.CrossRefGoogle Scholar
Bhaskar, K. R., Garik, P., Turner, B. S., Bradley, J. D., Bansil, R., Stanley, H. E. & LaMont, J. T. 1992 Viscous fingering of HCl through gastric mucin. Nature 360, 458–461.CrossRefGoogle ScholarPubMed
Bischofberger, I., Ramachandran, R. & Nagel, S. R. 2014 Fingering versus stability in the limit of zero interfacial tension. Nat. Commun. 5, 5265.CrossRefGoogle ScholarPubMed
Bongrand, G. & Tsai, P. A. 2018 Manipulation of viscous fingering in a radially tapered cell geometry. Phys. Rev. E 97, 061101(R).Google Scholar
Callan-Jones, A. C., Joanny, J.-F. & Prost, J. 2008 Viscous-fingering-like instability of cell fragments. Phys. Rev. Lett. 100, 258106.CrossRefGoogle ScholarPubMed
Chen, C.-Y., Huang, C.-W., Wang, L.-C. & Miranda, J. A. 2010 Controlling radial fingering patterns in miscible confined flows. Phys. Rev. E 82, 056308.Google ScholarPubMed
Cheng, N.-S. 2008 Formula for the viscosity of a glycerol–water mixture. Ind. Engng Chem. Res. 47 (9), 3285–3288.CrossRefGoogle Scholar
Chui, J. Y. Y., de Anna, P. & Juanes, R. 2015 Interface evolution during radial miscible viscous fingering. Phys. Rev. E 92, 041003(R).Google ScholarPubMed
D’Errico, G., Ortona, O., Capuano, F. & Vitagliano, V. 2004 Diffusion coefficients for the binary system glycerol + water at 25 °C. A velocity correlation study. J. Chem. Engng Data 49 (6), 1665–1670.CrossRefGoogle Scholar
Dias, E. O., Alvarez-Lacalle, E., Carvalho, M. S. & Miranda, J. A. 2012 Minimization of viscous fluid fingering: a variational scheme for optimal flow rates. Phys. Rev. Lett. 109, 144502.CrossRefGoogle ScholarPubMed
Escala, D. M., De Wit, A., Carballido-Landeira, J. & Muñuzuri, A. P. 2019 Viscous fingering induced by a pH-sensitive clock reaction. Langmuir 35 (11), 4182–4188.CrossRefGoogle ScholarPubMed
Guiochon, G., Felinger, A., Shirazi, D. G. & Katti, A. M. 2008 Fundamentals of Preparative and Nonlinear Chromatography, 2nd edn. Academic Press Elsevier.Google Scholar
Homsy, G. M. 1987 Viscous fingering in porous media. Annu. Rev. Fluid Mech. 19 (1), 271–311.CrossRefGoogle Scholar
Hota, T. K., Pramanik, S. & Mishra, M. 2015a Nonmodal linear stability analysis of miscible viscous fingering in porous media. Phys. Rev. E 92, 053007.Google Scholar
Hota, T. K., Pramanik, S. & Mishra, M. 2015b Onset of fingering instability in a finite slice of adsorbed solute. Phys. Rev. E 92, 023013.Google Scholar
Huang, Y.-S. & Chen, C.-Y. 2015 A numerical study on radial Hele-Shaw flow: influence of fluid miscibility and injection scheme. Comput. Mech. 55 (2), 407–420.CrossRefGoogle Scholar
Jha, B., Cueto-Felgueroso, L. & Juanes, R. 2011 Fluid mixing from viscous fingering. Phys. Rev. Lett. 106, 194502.CrossRefGoogle ScholarPubMed
Lake, L. W. 1989 Enhanced Oil Recovery. Prentice-Hall.Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103 (1), 16–42.CrossRefGoogle Scholar
Li, Q., Cai, W., Li, F.-C., Li, B. & Chen, C.-Y. 2019 Miscible density-driven flows in heterogeneous porous media: influences of correlation length and distribution of permeability. Phys. Rev. Fluids 4, 014502.CrossRefGoogle Scholar
Li, S., Lowengrub, J. S., Fontana, J. & Palffy-Muhoray, P. 2009 Control of viscous fingering patterns in a radial Hele-Shaw cell. Phys. Rev. Lett. 102, 174501.CrossRefGoogle Scholar
Matar, O. K. & Troian, S. M. 1999 Spreading of a surfactant monolayer on a thin liquid film: onset and evolution of digitated structures. Chaos 9 (1), 141–153.CrossRefGoogle ScholarPubMed
Mishra, M., Martin, M. & De Wit, A. 2008 Differences in miscible viscous fingering of finite width slices with positive or negative log-mobility ratio. Phys. Rev. E 78, 066306.Google ScholarPubMed
Moortgat, J. 2016 Viscous and gravitational fingering in multiphase compositional and compressible flow. Adv. Water Resour. 89, 53–66.CrossRefGoogle Scholar
Paterson, L. 1981 Radial fingering in a Hele-Shaw cell. J. Fluid Mech. 113, 513–529.CrossRefGoogle Scholar
Pihler-Puzović, D., Peng, G. G., Lister, J. R., Heil, M. & Juel, A. 2018 Viscous fingering in a radial elastic-walled Hele-Shaw cell. J. Fluid Mech. 849, 163–191.CrossRefGoogle Scholar
Pramanik, S. & Mishra, M. 2015 Effect of Péclet number on miscible rectilinear displacement in a Hele-Shaw cell. Phys. Rev. E 91, 033006.Google Scholar
Riaz, A., Pankiewitz, C. & Meiburg, E. 2004 Linear stability of radial displacements in porous media: influence of velocity-induced dispersion and concentration-dependent diffusion. Phys. Fluids 16 (10), 3592–3598.CrossRefGoogle Scholar
Schneider, C. A., Rasband, W. S. & Eliceiri, K. W. 2012 NIH Image to ImageJ: 25 years of image analysis. Nat. Meth. 9, 671–675.CrossRefGoogle ScholarPubMed
Sharma, V., Pramanik, S., Chen, C.-Y. & Mishra, M. 2019 A numerical study on reaction-induced radial fingering instability. J. Fluid Mech. 862, 624–638.CrossRefGoogle Scholar
Tan, C. T. & Homsy, G. M. 1987 Stability of miscible displacements in porous media: radial source flow. Phys. Fluids 30 (5), 1239–1245.CrossRefGoogle Scholar
Videbæk, T. E. & Nagel, S. R. 2019 Diffusion-driven transition between two regimes of viscous fingering. Phys. Rev. Fluids 4, 033902.CrossRefGoogle Scholar
Volk, A. & Kähler, C. J. 2018 Density model for aqueous glycerol solutions. Exp. Fluids 59 (5), 75.CrossRefGoogle Scholar
Witten, Jr., T. A, & Sander, L. M. 1981 Diffusion-limited aggregation, a kinetic critical phenomenon. Phys. Rev. Lett. 47, 1400–1403.Google Scholar
Yuan, Q., Zhou, X., Wang, J., Zeng, F., Knorr, K. D. & Imran, M. 2019 Control of viscous fingering and mixing in miscible displacements with time-dependent rates. AIChE J. 65 (1), 360–371.CrossRefGoogle Scholar
Zheng, Z., Kim, H. & Stone, H. A. 2015 Controlling viscous fingering using time-dependent strategies. Phys. Rev. Lett. 115, 174501.CrossRefGoogle ScholarPubMed