Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T20:30:59.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Development of gravity currents on rapidly changing slopes

Published online by Cambridge University Press:  02 November 2017

M. E. Negretti Open the ORCID record for M. E. Negretti [Opens in a new window] ,
J.-B. Flòr  and
E. J. Hopfinger
M. E. Negretti
Affiliation:
Univ. Grenoble Alpes, CNRS, LEGI, 38000 Grenoble, France
J.-B. Flòr
Affiliation:
Univ. Grenoble Alpes, CNRS, LEGI, 38000 Grenoble, France
E. J. Hopfinger
Affiliation:
Univ. Grenoble Alpes, CNRS, LEGI, 38000 Grenoble, France
Get access Rights & Permissions [Opens in a new window]

Abstract

Gravity currents often occur on complex topographies and are therefore subject to spatial development. We present experimental results on continuously supplied gravity currents moving from a horizontal to a sloping boundary, which is either concave or straight. The change in boundary slope and the consequent acceleration give rise to a transition from a stable subcritical current with a large Richardson number to a Kelvin–Helmholtz (KH) unstable current. 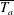It is shown here that depending on the overall acceleration parameter $\overline{T_{a}}$, expressing the rate of velocity increase, the currents can adjust gradually to the slope conditions (small 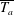$\overline{T_{a}}$) or go through acceleration–deceleration cycles (large 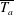$\overline{T_{a}}$). In the latter case, the KH billows at the interface have a strong effect on the flow dynamics, and are observed to cause boundary layer separation. Comparison of currents on concave and straight slopes reveals that the downhill deceleration on concave slopes has no qualitative influence, i.e. the dynamics is entirely dominated by the initial acceleration and ensuing KH billows. Following the similarity theory of Turner 1973 (Buoyancy Effects in Fluids. Cambridge University Press), we derive a general equation for the depth-integrated velocity that exhibits all driving and retarding forces. Comparison of this equation with the experimental velocity data shows that when 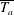$\overline{T_{a}}$ is large, bottom friction and entrainment are large in the region of appearance of KH billows. The large bottom friction is confirmed by the measured high Reynolds stresses in these regions. The head velocity does not exhibit the same behaviour as the layer velocity. It gradually approaches an equilibrium state even when the acceleration parameter of the layer is large.

JFM classification

Geophysical and Geological Flows: Gravity currents Geophysical and Geological Flows: Stratified flows Geophysical and Geological Flows: Topographic effects
Type
Papers
Information
Journal of Fluid Mechanics , Volume 833 , 25 December 2017 , pp. 70 - 97
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albayrak, I., Hopfinger, E. J. & Lemmin, U. 2008 Near-field flow structure of a confined wall jet on flat and concave rough walls. J. Fluid Mech. 606, 27–49.Google Scholar
Altinakar, M. S., Graf, W. H. & Hopfinger, E. J. 1990 Weakly depositing turbidity current on small slopes. J. Hydraul Res. 28/1, 22–80.Google Scholar
Armi, L. 1986 The hydraulics of two flowing layers with different densities. J. Fluid Mech. 163, 27–58.Google Scholar
Baringer, M. O. & Price, J. F. 2001 Mixing and spreading of the Mediterranean outflow. J. Phys. Oceanogr. 27, 1654–1677.Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics, p. 188. Cambridge University Press.Google Scholar
Beghin, P., Hopfinger, E. J. & Britter, R. 1981 Gravitational convection from instantaneous sources on inclined boundaries. J. Fluid Mech. 107, 407–422.Google Scholar
Britter, R. E. & Linden, P. F. 1980 The motion of the front of a gravity current travelling down an incline. J. Fluid Mech. 99 (3), 531–543.Google Scholar
Brun, C. 2017 Large-eddy simulation of katabatic jet along a convexly curved slope: 2. Evidence of Görtler vortices. J. Geophys. Res. Atmos. 122, 5190–5210.Google Scholar
Calder, E. S., Cole, P. D., Dade, W. B., Druitt, T. H., Hoblitt, R. P., Huppert, H. E., Ritchie, L., Sparks, R. S. J. & Young, S. R. 1999 Mobility of pyroclastic flows and surges at the Soufriere Hills Volcano, Montserrat. Geophys. Res. Lett. 26 (5), 537–540.Google Scholar
Corcos, G. M. & Sherman, F. S. 1976 Vorticity concentration and the dynamics of free shear layers. J. Fluid Mech. 79, 241–264.Google Scholar
Ellison, T. H. & Turner, J. S. 1959 Turbulent entrainment in stratified flows. J. Fluid Mech. 6 (3), 423–448.Google Scholar
Etienne, J., Rastello, M. & Hopfinger, E. J. 2006 Modelling and simulation of powder snow avalanches. C. R. Méc. 334, 545–554.CrossRefGoogle Scholar
Farmer, D. M. & Armi, L. 2001 Stratified flow over topography: the role of small scale entrainment and mixing in flow establishment. Proc. R. Soc. Lond. 455, 3221–3258.CrossRefGoogle Scholar
Fernando, H. J. S. 1999 Fluid dynamics of urban atmospheres in complex terrain. Annu. Rev. Fluid Mech. 379, 39–69.Google Scholar
Fernando, H. J. S. 2012 Handbook of Environmental Fluid Mechanics, vol. 2. CRC Press.Google Scholar
Haertel, C., Meiburg, E. & Necker, F. 2000 Analysis and direct numerical simulation of the flow at a gravity current head. Part I. Flow topology and front speed for slip and non-slip boundaries. J. Fluid Mech. 418, 189–212.Google Scholar
Hopfinger, E. J. 1983 Snow avalanche motion and related phenomena. Ann. Rev. Fluid Mech. 15, 47–76.Google Scholar
Hopfinger, E. J. & Tochon-Danguy, J. C. 1977 A model study of powder snow avalanches. J. Glaciol. 19 (81), 343–356.Google Scholar
Koop, C. G. & Browand, F. K. 1979 Instability and turbulence in a stratified fluid with shear. J. Fluid Mech. 93, 135–159.Google Scholar
Lilly, D. K. 1983 Stratified turbulence and the mesoscale variability in the atmosphere. J. Atm. Sci. 40, 749–761.Google Scholar
Luthi, S. 1990 Some new aspects of two dimensional turbidity currents. Sedimentology 28, 97–105.Google Scholar
Maxworthy, T. & Nokes, R. I. 2007 Experiments on gravity currents propagating down slopes. Part I. The release of a fixed volume of heavy fluid from an enclosed lock into an open channel. J. Fluid Mech. 584, 433–453.Google Scholar
Middleton, G. V. 1966 Small scale models for turbidity currents and the criterion of autosuspension. J. Sedim. Petrol. 36, 202–208.Google Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R, Soc. Lond. A 234 (1196), 1–23.Google Scholar
Parker, G., Fukushima, Y. & Pantin, H. M. 1986 Self accelerating turbidity currents. J. Fluid Mech. 171, 145–181.Google Scholar
Pawlak, G. & Armi, L. 2000 Mixing and entrainment in developing stratified currents. J. Fluid Mech. 424, 45–73.Google Scholar
Pope, S. B. 2000 Turbulent Flows, pp. 265–332. Cambridge University Press.Google Scholar
Rastello, M. & Hopfinger, E. J. 2004 Sediment-entraining suspension clouds: a model of powder-snow avalanches. J. Fluid Mech. 509, 181–206.Google Scholar
Ross, A. N., Dalziel, S. B. & Linden, P. F. 2006 Axisymmetric gravity currents on a cone. J. Fluid Mech. 565, 227–253.Google Scholar
Simpson, J. S. 1982 Gravity currents in the laboratory, atmosphere and ocean. Annu. Rev. Fluid Mech. 14, 213–234.Google Scholar
Swearingen, J. D. & Blackwelder, R. F. 1987 The growth and breakdown of streamwise vortices in the presence of a wall. J. Fluid Mech. 182, 255–290.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.Google Scholar
Wunsch, C. 2002 What is the thermohaline circulation. Science 298 (5596), 1179–1181.Google Scholar
Zhou, M. D., Heine, C. & Wygnanski, I. 1996 The effect of excitation on the coherent and random motion in a plane wall jet. J. Fluid Mech. 310, 1–37.Google Scholar