Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-09T03:44:26.651Z Has data issue: false hasContentIssue false
  • English
  • Français

Dispersion of gyrotactic micro-organisms in pipe flows

Published online by Cambridge University Press:  24 February 2020

Weiquan Jiang Open the ORCID record for Weiquan Jiang [Opens in a new window]  and
Guoqian Chen Open the ORCID record for Guoqian Chen [Opens in a new window]
Weiquan Jiang
Affiliation:
Laboratory of Systems Ecology and Sustainability Science, College of Engineering, Peking University, Beijing 100871, PR China
Guoqian Chen*
Affiliation:
Laboratory of Systems Ecology and Sustainability Science, College of Engineering, Peking University, Beijing 100871, PR China
*
†Email address for correspondence: gqchen@pku.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

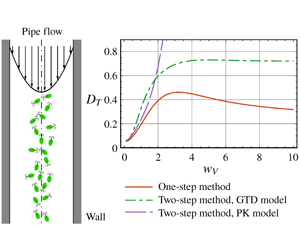
The transport of motile micro-organisms exhibits rich and complex phenomena, of significance to various biological and environmental applications. For dilute suspensions of gyrotactic algae dispersing in vertical pipe flows, previous studies obtained only approximate values for the overall drift and dispersivity in the longitudinal direction, using two-step averaging methods with the Pedley–Kessler (PK) model and the generalized Taylor dispersion (GTD) model. These two-step methods impose restrictive assumptions: both the swimming Péclet number and the variation of shear rates relative to swimming must be sufficiently small. Thus, it is difficult to analyse the gyrotactic dispersion process in the ‘breakdown’ parameter region. Following a recent study of Jiang & Chen (J. Fluid Mech., vol. 877, 2019, pp. 1–34), this paper applies the integrated and precise one-step GTD method to study the overall dispersion process and performs a quantitative test for the applicability of two-step methods. An appropriate function basis for series expansions in the GTD method is proposed to deal with reflective boundary conditions imposed at the tube wall. Detailed results for Chlamydomonas nivalis are presented to illustrate the influence of the gyrotactic focusing on the overall dispersion process, for both downwelling and upwelling flows. The overall drift above the mean flow increases monotonically with the flow rate. However, the overall dispersivity will first decrease, then increase, and finally saturate as the flow rate increases, due to a combined effect of gyrotaxis, swimming and convection. Shear alignments of prolate cells will weaken the focusing, and thus reduce the drift and enhance the dispersivity. The predictions by two-step methods with the PK and GTD models are found to be successful inside their required parameter region. Within the ‘breakdown’ region, the two-step GTD method still gives reasonable results for the local distribution and the drift, but fails in the predictions of dispersivity.

JFM classification

Biological Fluid Dynamics: Micro-organism dynamics Biological Fluid Dynamics: Swimming/flying
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 889 , 25 April 2020 , A18
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acién, F. G., Molina, E., Reis, A., Torzillo, G., Zittelli, G. C., Sepúlveda, C. & Masojídek, J. 2017 Photobioreactors for the production of microalgae. In Microalgae-Based Biofuels and Bioproducts (ed. Gonzalez-Fernandez, C. & Muñoz, R.), pp. 1–44. Woodhead Publishing.Google Scholar
Aris, R. 1956 On the dispersion of a solute in a fluid flowing through a tube. Proc. R. Soc. Lond. A 235 (1200), 67–77.Google Scholar
Bearon, R. N., Bees, M. A. & Croze, O. A. 2012 Biased swimming cells do not disperse in pipes as tracers: a population model based on microscale behaviour. Phys. Fluids 24 (12), 121902.CrossRefGoogle Scholar
Bearon, R. N., Hazel, A. L. & Thorn, G. J. 2011 The spatial distribution of gyrotactic swimming micro-organisms in laminar flow fields. J. Fluid Mech. 680, 602–635.CrossRefGoogle Scholar
Bees, M. A. & Croze, O. A. 2010 Dispersion of biased swimming micro-organisms in a fluid flowing through a tube. Proc. R. Soc. Lond. A 466 (2119), 2057–2077.CrossRefGoogle Scholar
Bees, M. A. & Croze, O. A. 2014 Mathematics for streamlined biofuel production from unicellular algae. Biofuels 5 (1), 53–65.CrossRefGoogle Scholar
Bees, M. A., Hill, N. A. & Pedley, T. J. 1998 Analytical approximations for the orientation distribution of small dipolar particles in steady shear flows. J. Math. Biol. 36 (3), 269–298.CrossRefGoogle Scholar
Berke, A. P., Turner, L., Berg, H. C. & Lauga, E. 2008 Hydrodynamic attraction of swimming microorganisms by surfaces. Phys. Rev. Lett. 101 (3), 038102.CrossRefGoogle ScholarPubMed
Bianchi, S., Saglimbeni, F. & Di Leonardo, R. 2017 Holographic imaging reveals the mechanism of wall entrapment in swimming bacteria. Phys. Rev. X 7 (1), 011010.Google Scholar
Brenner, H. 1982 A general theory of Taylor dispersion phenomena. II. An extension. Physico-Chem. Hydrodyn. 3 (2), 139–157.Google Scholar
Brenner, H. & Condiff, D. W. 1972 Transport mechanics in systems of orientable particles. III. Arbitrary particles. J. Colloid Interface Sci. 41 (2), 228–274.CrossRefGoogle Scholar
Cencini, M., Boffetta, G., Borgnino, M. & De Lillo, F. 2019 Gyrotactic phytoplankton in laminar and turbulent flows: a dynamical systems approach. Eur. Phys. J. E 42 (3), 31.Google ScholarPubMed
Chatwin, P. C. 1970 The approach to normality of the concentration distribution of a solute in a solvent flowing along a straight pipe. J. Fluid Mech. 43 (2), 321–352.CrossRefGoogle Scholar
Childress, S., Levandowsky, M. & Spiegel, E. A. 1975 Pattern formation in a suspension of swimming microorganisms: equations and stability theory. J. Fluid Mech. 69 (3), 591–613.CrossRefGoogle Scholar
Chisti, Y. 2007 Biodiesel from microalgae. Biotechnol. Adv. 25 (3), 294–306.CrossRefGoogle ScholarPubMed
Contino, M., Lushi, E., Tuval, I., Kantsler, V. & Polin, M. 2015 Microalgae scatter off solid surfaces by hydrodynamic and contact forces. Phys. Rev. Lett. 115 (25), 258102.CrossRefGoogle ScholarPubMed
Croze, O. A., Bearon, R. N. & Bees, M. A. 2017 Gyrotactic swimmer dispersion in pipe flow: testing the theory. J. Fluid Mech. 816, 481–506.CrossRefGoogle Scholar
Croze, O. A., Sardina, G., Ahmed, M., Bees, M. A. & Brandt, L. 2013 Dispersion of swimming algae in laminar and turbulent channel flows: consequences for photobioreactors. J. R. Soc. Interface 10 (81), 20121041.CrossRefGoogle ScholarPubMed
Doi, M. & Edwards, S. F. 1978 Dynamics of rod-like macromolecules in concentrated solution. Part 2. J. Chem. Soc. Faraday Trans. 74, 918–932.CrossRefGoogle Scholar
Doi, M. & Edwards, S. F. 1988 Brownian motion. In The Theory of Polymer Dynamics, pp. 46–90. Oxford University Press.Google Scholar
Drescher, K., Dunkel, J., Cisneros, L. H., Ganguly, S. & Goldstein, R. E. 2011 Fluid dynamics and noise in bacterial cell–cell and cell–surface scattering. Proc. Natl Acad. Sci. USA 108 (27), 10940–10945.CrossRefGoogle ScholarPubMed
Durham, W. M., Kessler, J. O. & Stocker, R. 2009 Disruption of vertical motility by shear triggers formation of thin phytoplankton layers. Science 323 (5917), 1067–1070.CrossRefGoogle ScholarPubMed
Durham, W. M. & Stocker, R. 2012 Thin phytoplankton layers: characteristics, mechanisms, and consequences. Annu. Rev. Mar. Sci. 4 (1), 177–207.CrossRefGoogle ScholarPubMed
Elgeti, J. & Gompper, G. 2013 Wall accumulation of self-propelled spheres. Eur. Phys. Lett. 101 (4), 48003.CrossRefGoogle Scholar
Ezhilan, B., Pahlavan, A. A. & Saintillan, D. 2012 Chaotic dynamics and oxygen transport in thin films of aerotactic bacteria. Phys. Fluids 24 (9), 091701.CrossRefGoogle Scholar
Ezhilan, B. & Saintillan, D. 2015 Transport of a dilute active suspension in pressure-driven channel flow. J. Fluid Mech. 777, 482–522.CrossRefGoogle Scholar
Fenchel, T. & Finlay, B. J. 1984 Geotaxis in the ciliated protozoon Loxodes. J. Expl Biol. 110 (1), 17–33.Google Scholar
Fenchel, T. & Finlay, B. J. 1986 Photobehavior of the ciliated protozoon Loxodes: taxic, transient, and kinetic responses in the presence and absence of oxygen. J. Protozool. 33 (2), 139–145.CrossRefGoogle Scholar
Frankel, I. & Brenner, H. 1989 On the foundations of generalized Taylor dispersion theory. J. Fluid Mech. 204, 97–119.CrossRefGoogle Scholar
Frankel, I. & Brenner, H. 1991 Generalized Taylor dispersion phenomena in unbounded homogeneous shear flows. J. Fluid Mech. 230, 147–181.CrossRefGoogle Scholar
Frankel, I. & Brenner, H. 1993 Taylor dispersion of orientable Brownian particles in unbounded homogeneous shear flows. J. Fluid Mech. 255, 129–156.CrossRefGoogle Scholar
Garcia, X., Rafaï, S. & Peyla, P. 2013 Light control of the flow of phototactic microswimmer suspensions. Phys. Rev. Lett. 110 (13), 138106.CrossRefGoogle ScholarPubMed
Goldstein, R. E. 2015 Green algae as model organisms for biological fluid dynamics. Annu. Rev. Fluid Mech. 47 (1), 343–375.CrossRefGoogle ScholarPubMed
Guo, J., Wu, X., Jiang, W. & Chen, G. 2018 Contaminant transport from point source on water surface in open channel flow with bed absorption. J. Hydrol. 561, 295–303.CrossRefGoogle Scholar
Hill, J., Kalkanci, O., McMurry, J. L. & Koser, H. 2007 Hydrodynamic surface interactions enable E. coli to seek efficient routes to swim upstream. Phys. Rev. Lett. 98 (6), 068101.CrossRefGoogle ScholarPubMed
Hill, N. A. & Bees, M. A. 2002 Taylor dispersion of gyrotactic swimming micro-organisms in a linear flow. Phys. Fluids 14 (8), 2598–2605.CrossRefGoogle Scholar
Hwang, Y. & Pedley, T. J. 2014a Bioconvection under uniform shear: linear stability analysis. J. Fluid Mech. 738, 522–562.CrossRefGoogle Scholar
Hwang, Y. & Pedley, T. J. 2014b Stability of downflowing gyrotactic microorganism suspensions in a two-dimensional vertical channel. J. Fluid Mech. 749, 750–777.CrossRefGoogle Scholar
Ishikawa, T. 2012 Vertical dispersion of model microorganisms in horizontal shear flow. J. Fluid Mech. 705, 98–119.CrossRefGoogle Scholar
Ishikawa, T. & Pedley, T. J. 2007 Diffusion of swimming model micro-organisms in a semi-dilute suspension. J. Fluid Mech. 588, 437–462.CrossRefGoogle Scholar
Ishikawa, T. & Pedley, T. J. 2008 Coherent structures in monolayers of swimming particles. Phys. Rev. Lett. 100 (8), 088103.CrossRefGoogle ScholarPubMed
Jakuszeit, T., Croze, O. A. & Bell, S. 2019 Diffusion of active particles in a complex environment: role of surface scattering. Phys. Rev. E 99 (1), 012610.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. 102 (715), 161–179.Google Scholar
Jiang, W. & Chen, G. 2019a Dispersion of active particles in confined unidirectional flows. J. Fluid Mech. 877, 1–34.CrossRefGoogle Scholar
Jiang, W. & Chen, G. 2019b Solute transport in two-zone packed tube flow: long-time asymptotic expansion. Phys. Fluids 31 (4), 043303.Google Scholar
Jiang, W. Q. & Chen, G. Q. 2018 Solution of Gill’s generalized dispersion model: solute transport in Poiseuille flow with wall absorption. Intl J. Heat Mass Transfer 127, 34–43.CrossRefGoogle Scholar
Kantsler, V., Dunkel, J., Polin, M. & Goldstein, R. E. 2013 Ciliary contact interactions dominate surface scattering of swimming eukaryotes. Proc. Natl Acad. Sci. USA 110 (4), 1187–1192.CrossRefGoogle ScholarPubMed
Kessler, J. O. 1984 Gyrotactic buoyant convection and spontaneous pattern formation in algal cell cultures. In Nonequilibrium Cooperative Phenomena in Physics and Related Fields (ed. Velarde, M. G.), pp. 241–248. Springer.CrossRefGoogle Scholar
Kessler, J. O. 1985 Hydrodynamic focusing of motile algal cells. Nature 313 (5999), 218–220.CrossRefGoogle Scholar
Kessler, J. O. 1986 Individual and collective fluid dynamics of swimming cells. J. Fluid Mech. 173, 191–205.CrossRefGoogle Scholar
Leal, L. G. & Hinch, E. J. 1972 The rheology of a suspension of nearly spherical particles subject to Brownian rotations. J. Fluid Mech. 55 (4), 745–765.CrossRefGoogle Scholar
Liao, Q., Li, L., Chen, R. & Zhu, X. 2014 A novel photobioreactor generating the light/dark cycle to improve microalgae cultivation. Bioresour. Technol. 161, 186–191.CrossRefGoogle ScholarPubMed
Lushi, E., Kantsler, V. & Goldstein, R. E. 2017 Scattering of biflagellate microswimmers from surfaces. Phys. Rev. E 96 (2), 023102.Google ScholarPubMed
Lushi, E., Wioland, H. & Goldstein, R. E. 2014 Fluid flows created by swimming bacteria drive self-organization in confined suspensions. Proc. Natl Acad. Sci. USA 111 (27), 9733–9738.CrossRefGoogle ScholarPubMed
Manela, A. & Frankel, I. 2003 Generalized Taylor dispersion in suspensions of gyrotactic swimming micro-organisms. J. Fluid Mech. 490, 99–127.CrossRefGoogle Scholar
Marchetti, M. C., Joanny, J. F., Ramaswamy, S., Liverpool, T. B., Prost, J., Rao, M. & Simha, R. A. 2013 Hydrodynamics of soft active matter. Rev. Mod. Phys. 85 (3), 1143–1189.CrossRefGoogle Scholar
Martin, M., Barzyk, A., Bertin, E., Peyla, P. & Rafai, S. 2016 Photofocusing: light and flow of phototactic microswimmer suspension. Phys. Rev. E 93 (5), 051101.Google ScholarPubMed
Mata, T. M., Martins, A. A. & Caetano, N. S. 2010 Microalgae for biodiesel production and other applications: a review. Renew. Sustain. Energy Rev. 14 (1), 217–232.CrossRefGoogle Scholar
Mathijssen, A. J. T. M., Shendruk, T. N., Yeomans, J. M. & Doostmohammadi, A. 2016 Upstream swimming in microbiological flows. Phys. Rev. Lett. 116 (2), 028104.CrossRefGoogle ScholarPubMed
Messiah, A. 2014 Appendix C. Vector addition coefficients and rotation matrices. In Quantum Mechanics, Unabridged reprint edn., pp. 1053–1078. Dover.Google Scholar
Muñoz, R. & Guieysse, B. 2006 Algal–bacterial processes for the treatment of hazardous contaminants: a review. Water Res. 40 (15), 2799–2815.Google ScholarPubMed
Nambiar, S., Phanikanth, S., Nott, P. R. & Subramanian, G. 2019 Stress relaxation in a dilute bacterial suspension: the active–passive transition. J. Fluid Mech. 870, 1072–1104.CrossRefGoogle Scholar
Olver, F. W. J., Lozier, D. W., Boisvert, R. F. & Clark, C. W.(Eds) 2010 NIST Handbook of Mathematical Functions. Cambridge University Press.Google Scholar
Pedley, T. J. 2010a Collective behaviour of swimming micro-organisms. Exp. Mech. 50 (9), 1293–1301.CrossRefGoogle Scholar
Pedley, T. J. 2010b Instability of uniform micro-organism suspensions revisited. J. Fluid Mech. 647, 335–359.CrossRefGoogle Scholar
Pedley, T. J., Hill, N. A. & Kessler, J. O. 1988 The growth of bioconvection patterns in a uniform suspension of gyrotactic micro-organisms. J. Fluid Mech. 195, 223–237.CrossRefGoogle Scholar
Pedley, T. J. & Kessler, J. O. 1990 A new continuum model for suspensions of gyrotactic micro-organisms. J. Fluid Mech. 212, 155–182.CrossRefGoogle ScholarPubMed
Pedley, T. J. & Kessler, J. O. 1992 Hydrodynamic phenomena in suspensions of swimming microorganisms. Annu. Rev. Fluid Mech. 24 (1), 313–358.CrossRefGoogle Scholar
Posten, C. 2009 Design principles of photo-bioreactors for cultivation of microalgae. Eng. Life Sci. 9 (3), 165–177.CrossRefGoogle Scholar
Risken, H. 1996 Fokker–Planck equation. In The Fokker–Planck Equation: Methods of Solution and Applications, 2nd edn. pp. 63–95. Springer.CrossRefGoogle Scholar
Rothschild, N. 1963 Non-random distribution of bull spermatozoa in a drop of sperm suspension. Nature 198 (4886), 1221–1222.CrossRefGoogle Scholar
Rusconi, R., Guasto, J. S. & Stocker, R. 2014 Bacterial transport suppressed by fluid shear. Nat. Phys. 10 (3), 212–217.CrossRefGoogle Scholar
Rusconi, R. & Stocker, R. 2015 Microbes in flow. Curr. Opin. Microbiol. 25, 1–8.CrossRefGoogle ScholarPubMed
Saintillan, D. 2018 Rheology of active fluids. Annu. Rev. Fluid Mech. 50 (1), 563–592.CrossRefGoogle Scholar
Santamaria, F., De Lillo, F., Cencini, M. & Boffetta, G. 2014 Gyrotactic trapping in laminar and turbulent Kolmogorov flow. Phys. Fluids 26 (11), 111901.CrossRefGoogle Scholar
Stephenson, A. L., Kazamia, E., Dennis, J. S., Howe, C. J., Scott, S. A. & Smith, A. G. 2010 Life-cycle assessment of potential algal biodiesel production in the United Kingdom: a comparison of raceways and air-lift tubular bioreactors. Energy Fuels 24 (7), 4062–4077.CrossRefGoogle Scholar
Strand, S. R. & Kim, S. 1992 Dynamics and rheology of a dilute suspension of dipolar nonspherical particles in an external field. Part 1. Steady shear flows. Rheol. Acta 31 (1), 94–117.CrossRefGoogle Scholar
Suresh Kumar, K., Dahms, H.-U., Won, E.-J., Lee, J.-S. & Shin, K.-H. 2015 Microalgae – a promising tool for heavy metal remediation. Ecotoxicol. Environ. Saf. 113, 329–352.CrossRefGoogle ScholarPubMed
Taylor, G. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. 219 (1137), 186–203.Google Scholar
Taylor, G. 1954 The dispersion of matter in turbulent flow through a pipe. Proc. R. Soc. Lond. 223 (1155), 446–468.Google Scholar
Volpe, G., Gigan, S. & Volpe, G. 2014 Simulation of the active Brownian motion of a microswimmer. Am. J. Phys. 82 (7), 659–664.CrossRefGoogle Scholar
Wang, P. & Chen, G. Q. 2017 Basic characteristics of Taylor dispersion in a laminar tube flow with wall absorption: exchange rate, advection velocity, dispersivity, skewness and kurtosis in their full time dependance. Intl J. Heat Mass Transfer 109, 844–852.CrossRefGoogle Scholar
Wu, Z. & Chen, G. Q. 2014 Approach to transverse uniformity of concentration distribution of a solute in a solvent flowing along a straight pipe. J. Fluid Mech. 740, 196–213.CrossRefGoogle Scholar
Yang, Y., Tan, S. W., Zeng, L., Wu, Y. H., Wang, P. & Jiang, W. Q. 2020 Migration of active particles in a surface flow constructed wetland. J. Hydrol. 582, 124523.CrossRefGoogle Scholar
Zeng, L. & Pedley, T. J. 2018 Distribution of gyrotactic micro-organisms in complex three-dimensional flows. Part 1. Horizontal shear flow past a vertical circular cylinder. J. Fluid Mech. 852, 358–397.CrossRefGoogle Scholar
Zeng, L., Zhang, H. W., Wu, Y. H., Li, C. F. & Wang, P. 2019 Theoretical and numerical analysis of vertical distribution of active particles in a free-surface wetland flow. J. Hydrol. 573, 449–455.CrossRefGoogle Scholar
Zöttl, A. & Stark, H. 2012 Nonlinear dynamics of a microswimmer in Poiseuille flow. Phys. Rev. Lett. 108 (21), 218104.CrossRefGoogle ScholarPubMed
Zöttl, A. & Stark, H. 2013 Periodic and quasiperiodic motion of an elongated microswimmer in Poiseuille flow. Eur. Phys. J. E 36 (1), 4.Google ScholarPubMed