Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-22T16:09:22.711Z Has data issue: false hasContentIssue false
  • English
  • Français

Dispersion of solute released from a sphere flowing in a microchannel

Published online by Cambridge University Press:  18 April 2017

Stephan Gekle Open the ORCID record for Stephan Gekle [Opens in a new window]
Stephan Gekle*
Affiliation:
Fachbereich Physik, Universität Bayreuth, 95440 Bayreuth, Germany
*
†Email address for correspondence: stephan.gekle@uni-bayreuth.de
Get access Rights & Permissions [Opens in a new window]

Abstract

A solute is released from the surface of a sphere flowing freely in a cylindrical channel mimicking a modern drug delivery agent in a blood vessel. The solute then disperses by the combined action of advection and diffusion. We consider reflecting boundary conditions on the sphere and absorbing boundary conditions on the channel surface mimicking a biochemical reaction between the drug and endothelial cells on the vessel surface. The drug is released either instantaneously or continuously in time. The two key observables are the mean residence time in the flow before the drug is absorbed and the width over which it is spread on the vessel surface upon reaction. We numerically solve the Fokker–Planck equation for the time-dependent substance concentration combined with an analytical solution of the flow field. As expected, we find that the presence of the sphere leads to a substantial reduction in mean residence time and reaction width. Surprisingly, however, even in the limit of very large Péclet numbers (high velocities) the sphere-free case is not generally recovered. This observation can be attributed mainly to the small, but non-negligible radial flow component induced by the moving sphere. We further identify a strong influence of the release position which sharply separates two qualitatively different regimes. If the release position is between 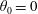$\unicode[STIX]{x1D703}_{0}=0$ (front) and a critical 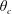$\unicode[STIX]{x1D703}_{c}$ the substance is quickly advected away from the sphere and its overall behaviour is similar to free diffusion in an empty channel. For release between 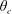$\unicode[STIX]{x1D703}_{c}$ and 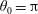$\unicode[STIX]{x1D703}_{0}=\unicode[STIX]{x03C0}$ (tail), on the other hand, the substance is pushed towards the sphere leading to behaviour reminiscent of confined diffusion between two infinitely long cylinders. The critical position 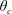$\unicode[STIX]{x1D703}_{c}$ is generally smaller than 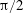$\unicode[STIX]{x03C0}/2$ which would correspond to an equatorial release position.

JFM classification

Biological Fluid Dynamics: Biomedical flows Biological Fluid Dynamics: Blood flow Biological Fluid Dynamics: Capsule/cell dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 819 , 25 May 2017 , pp. 104 - 120
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrover, A. 2011 Convection-dominated dispersion in channels with fractal cross-section. Phys. Fluids 23 (1), 013603.CrossRefGoogle Scholar
Adrover, A. 2013 Effect of secondary flows on dispersion in finite-length channels at high Peclet numbers. Phys. Fluids 25 (9), 093601.Google Scholar
Adrover, A. & Pedacchia, A. 2013 Mass transfer through laminar boundary layer in microchannels with nonuniform cross section: the effect of wall shape and curvature. Intl J. Heat Mass Transfer 60 (C), 624–631.CrossRefGoogle Scholar
Adrover, A. & Pedacchia, A. 2014 Mass/heat transfer through laminar boundary layer in axisymmetric microchannels with nonuniform cross section and fixed wall concentration/temperature. Intl J. Heat Mass Transfer 68 (C), 21–28.Google Scholar
Aris, R. 1956 On the dispersion of a solute in a fluid flowing through a tube. Proc. R. Soc. Lond. A 235 (1200), 67–77.Google Scholar
Balakotaiah, V. 2008 Comment on ‘Taylor dispersion with absorbing boundaries: a stochastic approach’. Phys. Rev. Lett. 100 (2), 029402.CrossRefGoogle ScholarPubMed
Balasubramanian, V., Jayaraman, G. & Iyengar, S. R. F. 1997 Effect of secondary flows on contaminant dispersion with weak boundary absorption. Appl. Math. Model. 21 (5), 275–285.CrossRefGoogle Scholar
Barton, N. G. 1984 An asymptotic theory for dispersion of reactive contaminants in parallel flow. J. Austral. Math. Soc. B 25, 287–310.CrossRefGoogle Scholar
Berezhkovskii, A. M. 2012 Note: Aris–Taylor dispersion from single-particle point of view. J. Chem. Phys. 137 (6), 066101.Google Scholar
Berezhkovskii, A. M. & Skvortsov, A. T. 2013 Aris–Taylor dispersion with drift and diffusion of particles on the tube wall. J. Chem. Phys. 139 (8), 084101.CrossRefGoogle ScholarPubMed
Bhaumik, S. K., Kannan, A. & Dasgupta, S. 2015 Taylor–Aris dispersion induced by axial variation in velocity profile in patterned microchannels. Chem. Engng Sci. 134 (C), 251–259.Google Scholar
Biswas, R. R. & Sen, P. N. 2007 Taylor dispersion with absorbing boundaries: a stochastic approach. Phys. Rev. Lett. 98 (16), 164501.Google Scholar
Biswas, R. R. & Sen, P. N. 2008 Biswas and Sen reply. Phys. Rev. Lett. 100 (2), 029403.Google Scholar
Camassa, R., Lin, Z. & McLaughlin, R. M. 2010 The exact evolution of the scalar variance in pipe and channel flow. Commun. Math. Sci. 8 (2), 601–626.Google Scholar
Chatwin, P. C. 1970 The approach to normality of the concentration distribution of a solute in a solvent flowing along a straight pipe. J. Fluid Mech. 43, 321–352.CrossRefGoogle Scholar
Daddi-Moussa-Ider, A. & Gekle, S. 2016 Hydrodynamic interaction between particles near elastic interfaces. J. Chem. Phys. 145 (1), 014905.Google Scholar
Daddi-Moussa-Ider, A., Guckenberger, A. & Gekle, S. 2016 Long-lived anomalous thermal diffusion induced by elastic cell membranes on nearby particles. Phys. Rev. E 93 (1), 012612.Google Scholar
Daddi-Moussa-Ider, A., Lisicki, M. & Gekle, S. 2017 Mobility of an axisymmetric particle near an elastic interface. J. Fluid Mech. 811, 210–233.CrossRefGoogle Scholar
Dagdug, L., Berezhkovskii, A. M. & Skvortsov, A. T. 2014 Aris–Taylor dispersion in tubes with dead ends. J. Chem. Phys. 141 (2), 024705.Google Scholar
Dagdug, L., Berezhkovskii, A. M. & Skvortsov, A. T. 2015 Trapping of diffusing particles by striped cylindrical surfaces. Boundary homogenization approach. J. Chem. Phys. 142 (23), 234902.Google Scholar
Davidson, M. R. & Schroter, R. C. 1983 A theoretical model of absorption of gases by the bronchial wall. J. Fluid Mech. 129, 313–335.Google Scholar
Deutch, J. M. 1980 A simple method for determining the mean passage time for diffusion. J. Chem. Phys. 73, 4700.Google Scholar
Dorfman, K. D. 2009 Taylor–Aris dispersion during lubrication flow in a periodic channel. Chem. Engng Commun. 197 (1), 39–50.CrossRefGoogle Scholar
Dorfman, K. D. & Brenner, H. 2008 Comment on ‘Taylor dispersion with absorbing boundaries: a stochastic approach’. Phys. Rev. Lett. 100 (2), 029401.CrossRefGoogle ScholarPubMed
Giona, M., Adrover, A., Cerbelli, S. & Garofalo, F. 2009 Laminar dispersion at high Péclet numbers in finite-length channels: effects of the near-wall velocity profile and connection with the generalized Leveque problem. Phys. Fluids 21 (12), 123601.CrossRefGoogle Scholar
Giona, M. & Cerbelli, S. 2010 Perturbation analysis of mixing and dispersion regimes in the low and intermediate Péclet number region. Phys. Rev. E 81 (4), 046309.Google Scholar
Giona, M. & Garofalo, F. 2015 Dispersion of overdamped diffusing particles in channel flows coupled to transverse acoustophoretic potentials: transport regimes and scaling anomalies. Phys. Rev. E 92 (3), 032104.Google ScholarPubMed
Hänggi, P., Talkner, P. & Borkovec, M. 1990 Reaction-rate theory: fifty years after Kramers. Rev. Mod. Phys. 62, 251–341.Google Scholar
Hansen, R., Bruus, H., Callisen, T. H. & Hassager, O. 2012 Transient convection, diffusion, and adsorption in surface-based biosensors. Langmuir 28 (19), 7557–7563.Google Scholar
Hlushkou, D., Gritti, F., Guiochon, G., Seidel-Morgenstern, A. & Tallarek, U. 2014 Effect of adsorption on solute dispersion: a microscopic stochastic approach. Anal. Chem. 86 (9), 4463–4470.Google Scholar
Howard, M. P., Gautam, A., Panagiotopoulos, A. Z. & Nikoubashman, A. 2016 Axial dispersion of Brownian colloids in microfluidic channels. Phys. Rev. Fluids 1 (4), 044203.Google Scholar
Jayaraman, G., Pedley, T. J. & Goyal, A. 1998 Dispersion of solute in a fluid flowing through a curved tube with absorbing walls. Q. J. Mech. Appl. Maths 51 (4), 577–598.Google Scholar
Kumar, J. P., Umavathi, J. C. & Basavaraj, A. 2012 Effects of homogeneous and heterogeneous reactions on the dispersion of a solute for immiscible viscous fluids between two plates. J.  Appl. Fluid Mech. 5 (4), 13–22.Google Scholar
Latini, M. & Bernoff, A. J. 2001 Transient anomalous diffusion in Poiseuille flow. J. Fluid Mech. 441, 399–411.Google Scholar
Leichtberg, S., Pfeffer, R. & Weinbaum, S. 1976 Stokes flow past finite coaxial clusters of spheres in a circular cylinder. Intl J. Multiphase Flow 3, 147.CrossRefGoogle Scholar
Lighthill, M. J. 1966 Initial development of diffusion in Poiseuille flow. IMA J. Appl. Maths 2 (1), 97–108.Google Scholar
Mazumder, B. S. & Das, S. K. 1992 Effect of boundary reaction on solute-dispersion in pulsatile flow through a tube. J. Fluid Mech. 239, 523–549.Google Scholar
Mazumder, B. S. & Paul, S. 2011 Dispersion of reactive species with reversible and irreversible wall reactions. Heat Mass Transfer 48 (6), 933–944.Google Scholar
Mondal, K. K. & Mazumder, B. S. 2005 On the solute dispersion in a pipe of annular cross-section with absorption boundary. Z. Angew. Math. Mech. 85 (6), 422–430.Google Scholar
Muradoglu, M. 2010 Axial dispersion in segmented gas–liquid flow: effects of alternating channel curvature. Phys. Fluids 22 (12), 122106.Google Scholar
Muradoglu, M., Günther, A. & Stone, H. A. 2007 A computational study of axial dispersion in segmented gas–liquid flow. Phys. Fluids 19 (7), 072109.Google Scholar
Nacev, A., Beni, C., Bruno, O. & Shapiro, B. 2011 The behaviors of ferromagnetic nano-particles in and around blood vessels under applied magnetic fields. J. Magn. Magn. Mater. 323 (6), 651–668.Google Scholar
Ng, C.-O. 2006 Dispersion in steady and oscillatory flows through a tube with reversible and irreversible wall reactions. Proc. R. Soc. Lond. A 462, 481–515.Google Scholar
Ng, C.-O. 2010 How does wall slippage affect hydrodynamic dispersion? Microfluid Nanofluid 10 (1), 47–57.Google Scholar
Ng, C.-O. & Rudraiah, N. 2008 Convective diffusion in steady flow through a tube with a retentive and absorptive wall. Phys. Fluids 20 (7), 073604.Google Scholar
Phillips, C. G. & Kaye, S. R. 1998 Approximate solutions for developing shear dispersion with exchange between phases. J. Fluid Mech. 374, 195–219.Google Scholar
Phillips, C. G., Kaye, S. R. & Robinson, C. D. 1995 Time-dependent transport by convection and diffusion with exchange between two phases. J. Fluid Mech. 297, 373–401.Google Scholar
Popel, A. S. & Johnson, P. C. 2005 Microcirculation and hemorheology. Annu. Rev. Fluid Mech. 37 (1), 43–69.Google Scholar
Purnama, A. 1988 Boundary retention effects upon contaminant dispersion in parallel flows. J. Fluid Mech. 195, 393–412.Google Scholar
Purnama, A. 1995 The dispersion of chemically active solutes in parallel-flow. J. Fluid Mech. 290, 263–277.Google Scholar
Ramachandra Rao, A. & Deshikachar, K. S. 1987 An exact analysis of unsteady convective diffusion in an annular pipe. Z. Angew. Math. Mech. 67 (3), 189–195.CrossRefGoogle Scholar
Sankarasubramanian, R. & Gill, W. N. 1971 Taylor diffusion in laminar flow in an eccentric annulus. Intl J. Heat Mass Transfer 14 (7), 905–919.Google Scholar
Sankarasubramanian, R. & Gill, W. N. 1973 Unsteady convective diffusion with interphase mass transfer. Proc. R. Soc. Lond. A 333, 115.Google Scholar
Sarkar, A. & Jayaraman, G. 2002 The effect of wall absorption on dispersion in annular flows. Acta Mechanica 158 (1–2), 105–119.Google Scholar
Skvortsov, A. T., Berezhkovskii, A. M. & Dagdug, L. 2015 Note: boundary homogenization for a circle with periodic absorbing arcs. Exact expression for the effective trapping rate. J. Chem. Phys. 143 (22), 226101.Google Scholar
Smith, R. 1983 Effect of boundary absorption upon longitudinal dispersion. J. Fluid Mech. 134, 161–177.Google Scholar
Szabo, A., Schulten, K. & Schulten, Z. 1980 First passage time approach to diffusion controlled reactions. J. Chem. Phys. 72, 4350.Google Scholar
Taylor, G. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219 (1137), 186–203.Google Scholar
Vedel, S. & Bruus, H. 2012 Transient Taylor–Aris dispersion for time-dependent flows in straight channels. J. Fluid Mech. 691, 95–122.CrossRefGoogle Scholar
Vedel, S., Hovad, E. & Bruus, H. 2014 Time-dependent Taylor–Aris dispersion of an initial point concentration. J. Fluid Mech. 752, 107–122.Google Scholar
Yeh, H. Y. & Keh, H. J. 2013 Axisymmetric creeping motion of a prolate particle in a cylindrical pore. Eur. J. Mech. (B/Fluids) 39, 52–58.CrossRefGoogle Scholar
Supplementary material: File

Gekle supplementary material

Gekle supplementary material 1

Download Gekle supplementary material(File)
File 928.4 KB