Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-24T17:44:30.590Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics and stability of the wake behind tandem cylinders sliding along a wall

Published online by Cambridge University Press:  28 March 2013

A. Rao ,
M. C. Thompson ,
T. Leweke  and
K. Hourigan
A. Rao
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia
M. C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia
T. Leweke*
Affiliation:
Institut de Recherche sur les Phénomènes Hors Équilibre (IRPHE), UMR 7342 CNRS, Aix-Marseille Université, 13384 Marseille, France
K. Hourigan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia Division of Biological Engineering, Monash University, Melbourne, Victoria 3800, Australia
*
†Email address for correspondence: thomas.leweke@irphe.univ-mrs.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

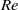The dynamics and stability of the flow past two cylinders sliding along a wall in a tandem configuration is studied numerically for Reynolds numbers ($\mathit{Re}$) between 20 and 200, and streamwise separation distances between 0.1 and 10 cylinder diameters. For cylinders at close separations, the onset of unsteady two-dimensional flow is delayed to higher 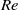$\mathit{Re}$ compared with the case of a single sliding cylinder, while at larger separations, this transition occurs earlier. For Reynolds numbers above the threshold, shedding from both cylinders is periodic and locked. At intermediate separation distances, the wake frequency shifts to the subharmonic of the leading-cylinder shedding frequency, which appears to be due to a feedback cycle, whereby shed leading-cylinder vortices interact strongly with the downstream cylinder to influence subsequent leading-cylinder shedding two cycles later. In addition to the shedding frequency, the drag coefficients for the two cylinders are determined for both the steady and unsteady regimes. The three-dimensional stability of the flow is also investigated. It is found that, when increasing the Reynolds number at intermediate separations, an initial three-dimensional instability develops, which disappears at higher 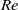$\mathit{Re}$. The new two-dimensional steady flow again becomes unstable, but with a different three-dimensional instability mode. At very close spacings, when the two cylinders are effectively seen by the flow as a single body, and at very large spacings, when the cylinders form independent wakes, the flow characteristics are similar to those of a single cylinder sliding along a wall.

JFM classification

Wakes/Jets: Wakes Vortex Flows: Vortex shedding Instability: Instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 722 , 10 May 2013 , pp. 291 - 316
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Bhattacharyya, S. & Dhinakaran, S. 2008 Vortex shedding in shear flow past tandem square cylinders in the vicinity of a plane wall. J. Fluids Struct. 24, 400–417.Google Scholar
Biermann, D. & Herrnstein, W. H. 1933 The interference of struts in various combinations. Tech. Rep. 468. National Advisory Committee for Aeronautics.Google Scholar
Blackburn, H. M. & Lopez, J. M. 2003 On three-dimensional quasi-periodic Floquet instabilities of two-dimensional bluff body wakes. Phys. Fluids 15, L57–L60.CrossRefGoogle Scholar
Carmo, B. S., Meneghini, J. R. & Sherwin, S. J. 2010 Secondary instabilities in the flow around two circular cylinders in tandem. J. Fluid Mech. 644, 395–431.Google Scholar
Carmo, B. S., Sherwin, S. J., Bearman, P. W. & Willden, R. H. J. 2008 Wake transition in the flow around two circular cylinders in staggered arrangements. J. Fluid Mech. 597, 1–29.CrossRefGoogle Scholar
Chorin, A. J. 1968 Numerical solution of the Navier–Stokes equations. Maths Comput. 22, 745–762.CrossRefGoogle Scholar
Deng, J., Ren, A.-L., Zou, J.-F. & Shao, X.-M. 2006 Three-dimensional flow around two circular cylinders in tandem arrangement. Fluid Dyn. Res. 38, 386–404.Google Scholar
Didier, E. 2007 Simulation de l’écoulement autour de deux cylindres en tandem. C. R. Mécanique 335, 696–701.Google Scholar
Elston, J. R., Blackburn, H. M. & Sheridan, J. 2006 The primary and secondary instabilities of flow generated by an oscillating circular cylinder. J. Fluid Mech. 550, 359–389.Google Scholar
Griffith, M. D., Leweke, T., Thompson, M. C. & Hourigan, K. 2009 Pulsatile flow in stenotic geometries: flow behaviour and stability. J. Fluid Mech. 622, 291–320.Google Scholar
Harichandan, A. B. & Roy, A. 2010 Numerical investigation of low Reynolds number flow past two and three circular cylinders using unstructured grid CFR scheme. Intl J. Heat Fluid Flow 31, 154–171.CrossRefGoogle Scholar
Harichandan, A. B. & Roy, A. 2012 Numerical investigation of flow past single and tandem cylindrical bodies in the vicinity of a plane wall. J. Fluids Struct. 33, 19–43.Google Scholar
Henderson, R. D. 1997 Non-linear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.Google Scholar
Hourigan, K., Thompson, M. C. & Tan, B. T. 2001 Self-sustained oscillations in flows around long flat plates. J. Fluids Struct. 15, 387–398.CrossRefGoogle Scholar
Huang, W.-X. & Sung, H. J. 2007 Vortex shedding from a circular cylinder near a moving wall. J. Fluids Struct. 23, 1064–1076.Google Scholar
Igarashi, T. 1981 Characteristics of flow around two circular cylinders arranged in tandem. Bull. JSME 24, 323–331.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97, 414–443.Google Scholar
Karniadakis, G. E. & Sherwin, S. J. 2005 Spectral/HP Methods for Computational Fluid Dynamics. Oxford University Press.Google Scholar
Karniadakis, G. E. & Triantafyllou, G. S. 1992 Three-dimensional dynamics and transition to turbulence in the wake of bluff objects. J. Fluid Mech. 238, 1–30.Google Scholar
Kevlahan, N. K. R. 2007 Three-dimensional Floquet stability analysis of the wake in cylinder arrays. J. Fluid Mech. 592, 79–88.Google Scholar
Kumar, S. R., Sjarma, A. & Agrawal, A. 2008 Simulation of flow around a row of square cylinders. J. Fluid Mech. 606, 369–397.Google Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2007 Three-dimensional transition in the wake of a transversely oscillating cylinder. J. Fluid Mech. 577, 79–104.Google Scholar
Liang, C., Papapdakis, G. & Luo, X. 2008 Effect of tube spacing on the vortex shedding characteristics of laminar flow past an inline tube array: a numerical study. Comput. Fluids 38, 950–964.Google Scholar
Mahir, N. 2009 Three-dimensional flow around a square cylinder near a wall. Ocean Engng 36, 357–367.Google Scholar
Mamun, C. K. & Tuckerman, L. S. 1995 Asymmetry and Hopf-bifurcation in spherical Couette flow. Phys. Fluids 7, 80–91.CrossRefGoogle Scholar
Meneghini, J. R., Saltara, F., Siqueira, C. L. R. & Ferrari, J. A. 2001 Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements. J. Fluids Struct. 15, 327–350.Google Scholar
Mittal, R & Balachandar, S 1995 Generation of streamwise vortical structures in bluff body wakes. Phys. Rev. Lett. 75, 1300–1303.Google Scholar
Mittal, S, Kumar, V & Raghuvanshi, A 1997 Unsteady incompressible flow past two cylinders in tandem and staggered arrangements. Intl J. Numer. Meth. Fluids 25, 1315–1344.3.0.CO;2-P>CrossRefGoogle Scholar
Mizushimaa, J. & Suehiro, N. 2005 Instability and transition of flow past two tandem circular cylinders. Phys. Fluids 17, 104107.Google Scholar
Mussa, A., Asinari, P. & Luo, L.-S. 2009 Lattice Boltzmann simulations of 2D laminar flows past two tandem cylinders. J. Comput. Phys. 228, 983–999.Google Scholar
Norberg, C 2003 Fluctuating lift on a circular cylinder: review and new measurements. J. Fluids Struct. 17, 57–96.Google Scholar
Papaioannou, G  V, Yue, D K  P, Triantafyllou, M  S & Karniadakis, G  E 2005 Three-dimensional flow around two circular cylinders in tandem arrangement. J. Fluid Mech. 558, 387–413.CrossRefGoogle Scholar
Rao, A., Passaggia, P.-Y., Bolnot, H., Thompson, M. C., Leweke, T. & Hourigan, K. 2012 Transition to chaos in the wake of a rolling sphere. J. Fluid Mech. 695, 135–148.Google Scholar
Rao, A, Stewart, B  E, Thompson, M  C, Leweke, T & Hourigan, K 2011 Flows past rotating cylinders next to a wall. J. Fluids Struct. 27, 668–679.Google Scholar
Ryan, K, Thompson, M  C & Hourigan, K 2005 Three-dimensional transition in the wake of bluff elongated cylinders. J. Fluid Mech. 538, 1–29.CrossRefGoogle Scholar
Sewatkar, C  M, Patel, R, Sharma, A & Agrawal, A 2012 Flow around six in-line square cylinders. J. Fluid Mech. 710, 195–233.Google Scholar
Sheard, G  J 2011 Wake stability features behind a square cylinder: focus on small incidence angles. J. Fluids Struct. 27, 734–742.CrossRefGoogle Scholar
Sheard, G. J., Fitzgerald, M. J. & Ryan, K. 2009 Cylinders with square cross-section: wake instabilities with incidence angle variation. J. Fluid Mech. 630, 43–69.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2003 From spheres to circular cylinders: the stability and flow structures of bluff ring wakes. J. Fluid Mech. 492, 147–180.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2005 Subharmonic mechanism of the mode C instability. Phys. Fluids 17, 111702.Google Scholar
Stewart, B. E., Hourigan, K., Thompson, M. C. & Leweke, T. 2006 Flow dynamics and forces associated with a cylinder rolling along a wall. Phys. Fluids 18, 111701.Google Scholar
Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2010a Numerical and experimental studies of the rolling sphere wake. J. Fluid Mech. 643, 137–162.Google Scholar
Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2010b The wake behind a cylinder rolling on a wall at varying rotation rates. J. Fluid Mech. 648, 225–256.Google Scholar
Thompson, M. C., Hourigan, K., Cheung, A. & Leweke, T. 2006a Hydrodynamics of a particle impact on a wall. Appl. Math. Model 30, 1356–1369.Google Scholar
Thompson, M. C., Hourigan, K., Ryan, K. & Sheard, G. J. 2006b Wake transition of two-dimensional cylinders and axisymmetric bluff bodies. J. Fluids Struct. 22, 793–806.Google Scholar
Thompson, M. C., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12, 190–196.Google Scholar
Thompson, M. C., Leweke, T. & Hourigan, K. 2007 Sphere–wall collisions: vortex dynamics and stability. J. Fluid Mech. 575, 121–148.Google Scholar
Thompson, M. C., Leweke, T. & Williamson, C. H. K. 2001 The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15, 607–616.Google Scholar
Williamson, C. H. K. 1988 The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31, 3165–3168.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Xu, G. & Zhou, Y. 2004 Strouhal numbers in the wake of two inline cylinders. Exp. Fluids 37, 248–256.Google Scholar
Zdravkovich, M. M. 1987 The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1, 239–261.Google Scholar
Zeng, L., Balachandar, S. & Fischer, P. 2005 Wall-induced forces on a rigid sphere at finite Reynolds number. J. Fluid Mech. 536, 1–25.Google Scholar
Zhang, H. Q., Noack, B. R., König, M. & Eckelmann, H. 1995 On the transition of the cylinder wake. Phys. Fluids 7, 779–793.Google Scholar
Zhou, Y. & Yiu, M. W. 2005 Flow structure, momentum and heat transport in a two-tandem-cylinder wake. J. Fluid Mech. 548, 17–48.Google Scholar