Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-12-01T06:42:32.508Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of helicity in homogeneous skew-isotropic turbulence

Published online by Cambridge University Press:  25 May 2017

Antoine Briard  and
Thomas Gomez Open the ORCID record for Thomas Gomez [Opens in a new window]
Antoine Briard
Affiliation:
$\unicode[STIX]{x2202}$’Alembert, CNRS UMR 7190, 4 Place Jussieu, F-75252 Paris CEDEX 5, France
Thomas Gomez*
Affiliation:
USTL, LML, F-59650 Villeneuve d’Ascq, France
*
†Email address for correspondence: thomas.gomez@univ-lille1.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics of helicity in homogeneous skew-isotropic freely decaying turbulence is investigated, at very high Reynolds numbers, thanks to a classical eddy-damped quasi-normal Markovian (EDQNM) closure. In agreement with previous direct numerical simulations, a 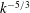$k^{-5/3}$ inertial range is obtained for both the kinetic energy and helical spectra. In the early stage of the decay, when kinetic energy, initially only present at large scales cascades towards small scales, it is found that helicity slightly slows down the nonlinear transfers. Then, when the turbulence is fully developed, theoretical decay exponents are derived and assessed numerically for helicity. Furthermore, it is found that the presence of helicity does not modify the decay rate of the kinetic energy with respect to purely isotropic turbulence, except in Batchelor turbulence where the kinetic energy decays slightly more rapidly. In this case, non-local expansions are used to show analytically that the permanence of the large eddies hypothesis is verified for the helical spectrum, unlike the kinetic energy one. Moreover, the 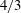$4/3$ law for the two-point helical structure function is assessed numerically at very large Reynolds numbers. Afterwards, the evolution equation of the helicity dissipation rate is investigated analytically, which provides significant simplifications and leads notably to the definition of a helical derivative skewness and of a helical Taylor scale, which is numerically very close to the classical Taylor longitudinal scale at large Reynolds numbers. Finally, when both a mean scalar gradient and helicity are combined, the quadrature spectrum, linked to the antisymmetric part of the scalar flux, appears and scales like 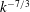$k^{-7/3}$ and then like 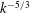$k^{-5/3}$ in the inertial range.

JFM classification

Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 821 , 25 June 2017 , pp. 539 - 581
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexakis, A. 2017 Helically decomposed turbulence. J. Fluid Mech. 812, 752–770.CrossRefGoogle Scholar
André, J. C. & Lesieur, M. 1977 Influence of helicity on the evolution of isotropic turbulence at high Reynolds number. J. Fluid Mech. 81, 187–207.CrossRefGoogle Scholar
Antonia, R. A., Ould-Rouis, M., Anselmet, F. & Zhu, Y. 1997 Analogy between predictions of Kolmogorov and Yaglom. J. Fluid Mech. 332, 395–409.Google Scholar
Baerenzung, J., Politano, H., Ponty, Y. & Pouquet, A. 2008 Spectral modeling of turbulent flows and the role of helicity. Phys. Rev. E 77 (5), 046303.Google ScholarPubMed
Biferale, L., Musacchio, S. & Toschi, F. 2012 Inverse energy cascade in three-dimensional isotropic turbulence. Phys. Rev. Lett. 108, 164501.CrossRefGoogle ScholarPubMed
Biferale, L., Musacchio, S. & Toschi, F. 2013 Split energy helicity cascades in three-dimensional homogeneous and isotropic turbulence. J. Fluid Mech. 730, 309–327.CrossRefGoogle Scholar
Borue, V. & Orszag, A. 1997 Spectra in helical three-dimensional homogeneous isotropic turbulence. Phys. Rev. E 55 (6), 7005–7009.Google Scholar
Bos, W. J. T., Chevillard, L., Scott, J. F. & Rubinstein, R. 2012 Reynolds number effect on the velocity increment skewness in isotropic turbulence. Phys. Fluids 24, 015108.Google Scholar
Briard, A., Gomez, T. & Cambon, C. 2016 Spectral modelling for passive scalar dynamics in homogeneous anisotropic turbulence. J. Fluid Mech. 799, 159–199.Google Scholar
Briard, A., Gomez, T., Sagaut, P. & Memari, S. 2015 Passive scalar decay laws in isotropic turbulence: Prandtl effects. J. Fluid Mech. 784, 274–303.CrossRefGoogle Scholar
Briard, A., Iyer, M. & Gomez, T. 2017 Anisotropic spectral modelling for unstably stratified homogeneous turbulence. Phys. Rev. Fluids 2 (4), 044604.CrossRefGoogle Scholar
Brissaud, A., Frisch, U., Leorat, J., Lesieur, M. & Mazure, A. 1973 Helicity cascades in fully developed isotropic turbulence. Phys. Fluids 16 (8), 1366–1367.CrossRefGoogle Scholar
Burlot, A., Gra, B.-J., Godeferd, F. S., Cambon, C. & Griffond, J. 2015 Spectral modelling of high Reynolds number unstably stratified homogeneous turbulence. J. Fluid Mech. 765, 17–44.Google Scholar
Cambon, C., Danaila, L., Godeferd, F. S. & Scott, J. F. 2013 Third-order statistics and the dynamics of strongly anisotropic turbulent flows. J. Turbul. 14 (3), 121–160.CrossRefGoogle Scholar
Cambon, C. & Jacquin, L. 1989 Spectral approach to non-isotropic turbulence subjected to rotation. J. Fluid Mech. 202, 295–317.CrossRefGoogle Scholar
Chen, Q., Chen, S. & Eyink, G. L. 2003 The joint cascade of energy and helicity in three-dimensional turbulence. Phys. Fluids 15 (2), 361–374.Google Scholar
Chkhetiani, O. G. 1996 On the third moments in helical turbulence. J. Expl Theor. Phys. Lett. 63, 808–812.Google Scholar
Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of a grid generated turbulence. J. Fluid Mech. 25, 657–682.Google Scholar
Ditlevsen, P. D. & Giuliani, P. 2001 Dissipation in helical turbulence. Phys. Fluids 13, 3508.Google Scholar
Eyink, G. L. & Thomson, D. J. 2000 Free decay of turbulence and breakdown of self-similarity. Phys. Fluids 12, 477–479.Google Scholar
George, W. K. 1992 The decay of homogeneous isotropic turbulence. Phys. Fluids A 7, 1492–1509.Google Scholar
George, W. K. & Hussein, H. J. 1991 Locally axisymmetric turbulence. J. Fluid Mech. 233, 1–23.CrossRefGoogle Scholar
Gomez, T., Politano, H. & Pouquet, A. 2000 Exact relationship for third-order structure functions in helical flows. Phys. Rev. E 61 (5), 5321–5325.Google Scholar
Gotoh, T. & Watanabe, T. 2015 Power and nonpower laws of passive scalar moments convected by isotropic turbulence. Phys. Rev. Lett. 115, 114502.Google Scholar
von Kármán, T. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. A 164 (917), 192–215.Google Scholar
Kerr, R. M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–58.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301–305.Google Scholar
Kraichnan, R. H. 1967 Inertial ranges in two dimensional turbulence. Phys. Fluids 10 (7), 1417–1423.Google Scholar
Kraichnan, R. H. 1973 Helical turbulence and absolute equilibrium. J. Fluid Mech. 59, 745–752.Google Scholar
Kurien, S. 2003 The reflection-antisymmetric counterpart of the Kármán Howarth dynamical equation. Physica D 175, 167–176.Google Scholar
Kurien, S., Taylor, M. A. & Matsumoto, T. 2004a Cascade time scales for energy and helicity in homogeneous isotropic turbulence. Phys. Rev. E 69, 066313.Google ScholarPubMed
Kurien, S., Taylor, M. A. & Matsumoto, T. 2004b Isotropic third-order statistics in turbulence with helicity: the 2/15-law. J. Fluid Mech. 515, 87–97.Google Scholar
Leith, C. E. 1971 Atmospheric predictability and two-dimensional turbulence. J. Atmos. Sci. 28 (2), 145–161.Google Scholar
Lesieur, M. 2008 Turbulence in Fluids, 4th edn. Martinus Nijhoff publishers.Google Scholar
Lesieur, M. & Ossia, S. 2000 3D isotropic turbulence at very high Reynolds numbers: Edqnm study. J. Turbul. 1 (7), 1–25.Google Scholar
Lesieur, M. & Schertzer, D. 1978 Amortissement auto similaire d’une turbulence à grand nombre de Reynolds. J. Mécanique 17 (4), 609–646.Google Scholar
Levshin, A. O. & Chkhetiani, O. G. 2013 Decay of helicity in homogeneous turbulence. Lett. J. Expl Theor. Phys. 90 (10), 598–602.Google Scholar
Meldi, M. & Sagaut, P. 2013 Further insights into self-similarity and self-preservation in freely decaying isotropic turbulence. J. Turbul. 14, 24–53.Google Scholar
Moffatt, H. K. 1969 The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35, 117–129.Google Scholar
Moffatt, H. K. & Tsinober, A. 1992 Helicity in laminar and turbulent flow. Annu. Rev. Fluid Mech. 24, 281–312.Google Scholar
Monin, A. S., Yaglom, A. M. & Lumley, J. L. 2007 Statistical Fluid Mechanics: Mechanics of Turbulence. Dover Books on Physics 2. Dover.Google Scholar
Mons, V., Cambon, C. & Sagaut, P. 2016 A spectral model for homogeneous shear-driven anisotropic turbulence in terms of spherically-averaged descriptors. J. Fluid Mech. 788, 147–182.Google Scholar
Mydlarski, L. & Warhaft, Z. 1998 Passive scalar statistics in high-Péclet-number grid turbulence. J. Fluid Mech. 358, 135–175.CrossRefGoogle Scholar
O’Gorman, P. A. & Pullin, D. I. 2005 Effect of schmidt number on the velocity scalar cospectrum in isotropic turbulence with a mean scalar gradient. J. Fluid Mech. 532, 111–140.Google Scholar
Orszag, S. A. 1970 Analytical theories of turbulence. J. Fluid Mech. 363–386.Google Scholar
Orszag, S. A. 1977 The statistical theory of turbulence. In Fluid Dynamics (ed. Balian, A. & Peube, J. L.), pp. 237–374. Gordon and Breach.Google Scholar
Polifke, W. 1991 Statistics of helicity fluctuations in homogeneous turbulence. Phys. Fluids A 3, 115–129.Google Scholar
Polifke, W. & Shtilman, L. 1989 The dynamics of helical decaying turbulence. Phys. Fluids A 1 (12), 2025–2033.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Pouquet, A., Frisch, U. & Léorat, J. 1976 Strong mhd helical turbulence and the nonlinear dynamo effect. J. Fluid Mech. 77, 321–354.Google Scholar
Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.Google Scholar
Watanabe, T. & Gotoh, T. 2004 Statistics of a passive scalar in homogeneous turbulence. New J. Phys. 6 (1), 40.Google Scholar
Yaglom, A. M. 1949 On the local structure of a temperature field in a turbulent flow. Dokl. Akad. Nauk SSSR 69, 743–746.Google Scholar
Yeung, P. K., Donzis, D. A. & Sreenivasan, K. R. 2005 High-Reynolds-number simulation of turbulent mixing. Phys. Fluids 17, 081703.Google Scholar
Yeung, P. K., Xu, S. & Sreenivasan, K. R. 2002 Schmidt number effects on turbulent transport with uniform mean scalar gradient. Phys. Fluids 14 (12), 4178–4191.Google Scholar