Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-19T15:39:03.132Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of robust structures in turbulent swirling reacting flows

Published online by Cambridge University Press:  08 March 2017

S. Roy Open the ORCID record for S. Roy [Opens in a new window] ,
T. Yi ,
N. Jiang ,
G. H. Gunaratne ,
I. Chterev ,
B. Emerson ,
T. Lieuwen ,
A. W. Caswell  and
J. R. Gord
S. Roy*
Affiliation:
Spectral Energies, LLC, 5100 Springfield Street, Suite 301, Dayton, OH 45431, USA
T. Yi
Affiliation:
Spectral Energies, LLC, 5100 Springfield Street, Suite 301, Dayton, OH 45431, USA
N. Jiang
Affiliation:
Spectral Energies, LLC, 5100 Springfield Street, Suite 301, Dayton, OH 45431, USA
G. H. Gunaratne*
Affiliation:
Department of Physics, University of Houston, Houston, TX 77204, USA
I. Chterev
Affiliation:
Ben T. Zinn Combustion Laboratory, Georgia Institute of Technology, Atlanta, GA 30332, USA
B. Emerson
Affiliation:
Ben T. Zinn Combustion Laboratory, Georgia Institute of Technology, Atlanta, GA 30332, USA
T. Lieuwen*
Affiliation:
Ben T. Zinn Combustion Laboratory, Georgia Institute of Technology, Atlanta, GA 30332, USA
A. W. Caswell
Affiliation:
Aerospace Systems Directorate, Air Force Research Laboratory, Wright-Patterson AFB, OH 45433, USA
J. R. Gord*
Affiliation:
Aerospace Systems Directorate, Air Force Research Laboratory, Wright-Patterson AFB, OH 45433, USA
*
†Email addresses for correspondence: roy.sukesh@gmail.com, phys57@central.uh.edu, tim.lieuwen@aerospace.gatech.edu, james.gord@us.af.mil
†Email addresses for correspondence: roy.sukesh@gmail.com, phys57@central.uh.edu, tim.lieuwen@aerospace.gatech.edu, james.gord@us.af.mil
†Email addresses for correspondence: roy.sukesh@gmail.com, phys57@central.uh.edu, tim.lieuwen@aerospace.gatech.edu, james.gord@us.af.mil
†Email addresses for correspondence: roy.sukesh@gmail.com, phys57@central.uh.edu, tim.lieuwen@aerospace.gatech.edu, james.gord@us.af.mil
Get access Rights & Permissions [Opens in a new window]

Abstract

High-speed synchronized stereo particle-imaging velocimetry and OH planar laser-induced fluorescence (PIV/OH-PLIF) measurements are performed on multiple 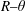$R{-}\unicode[STIX]{x1D703}$ planes downstream of a high-Reynolds-number swirling jet. Dynamic-mode decomposition (DMD) – a frequency-resolved data-reduction technique – is used to identify and characterize recurrent flow structures. Illustrative results are presented in a swirling flow field for two cases – the nominal flow dynamics and where self-excited combustion driven oscillations provide strong axisymmetric narrowband forcing of the flow. The robust constituent of the nominal reacting swirl flow corresponds to a helical shear-layer disturbance at a Strouhal number (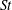$St$) of 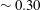${\sim}0.30$, 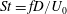$St=fD/U_{0}$, where 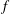$f$, 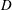$D$ and 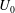$U_{0}$ denote the precessing vortex core (PVC) frequency (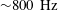${\sim}800~\text{Hz}$), the swirler exit diameter (19 mm) and the bulk velocity at the swirler exit (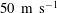$50~\text{m}~\text{s}^{-1}$) respectively. Planar projections of the PVC reveal a pair of oscillating skew-symmetric regions of velocity, vorticity and OH-PLIF intensity that rotate in the same direction as the mean tangential flow. During combustion instabilities, the large-amplitude acoustics-induced axisymmetric forcing of the flow results in a fundamentally different flow response dominated by a nearly axisymmetric disturbance and almost complete suppression of the large-scale helical shear-layer disturbances dominating the nominal flow. In addition, reverse axial flows around the centreline are significantly reduced. Time traces of the robust constituent show reverse axial flows around the centreline and negative axial vorticity along the inner swirling shear layer when the planar velocity is in the same direction as the mean tangential flow. For both stable and unstable combustion, recurrent flow structures decay rapidly downstream of the air swirler, as revealed by the decreasing amplitude of the velocity, axial vorticity and OH-PLIF intensity.

JFM classification

Reacting Flows: Combustion Reacting Flows: Turbulent reacting flows Vortex Flows: Vortex instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 816 , 10 April 2017 , pp. 554 - 585
Check for updates
Copyright
© Cambridge University Press 2017. This is a work of the U.S. Government and is not subject to copyright protection in the United States. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acharya, V., Malanoski, M., Aguilar, M. & Lieuwen, T. 2014 Dynamics of a transversely excited swirling, lifted flame: flame response modelling and comparison with experiments. Trans. ASME J. Engng Gas Turbines Power 136, 051503.Google Scholar
An, Q., Kwong, W., Geraedts, B. & Steinberg, A. M. 2016 Coupled dynamics of lift-off and precessing vortex core formation in swirl flames. Combust. Flame 168, 228–239.Google Scholar
Arndt, C. M., Severin, M., Dem, C., Stöhr, M., Steinberg, A. M. & Meier, W. 2015 Experimental analysis of thermo-acoustic instabilities in a generic gas turbine combustor by phase-correlated PIV, chemiluminescence, and laser Raman scattering measurements. Exp. Fluids 56, 69.Google Scholar
Balachandran, R., Dowling, A. P. & Mastirakos, E. 2008 Non-linear response of turbulent premixed flames to imposed inlet velocity oscillations of two frequencies. Flow Turbul. Combust. 80, 455–487.Google Scholar
Benjamin, T. B. 1967 Some developments in the theory of vortex breakdown. J. Fluid Mech. 28 (1), 65–84.Google Scholar
Boxx, I., Stöhr, M., Carter, C. D. & Meier, W. 2010 Temporally resolved planar measurements of transient phenomena in a partially pre-mixed swirl flame in a gas turbine model combustor. Combust. Flame 157, 1510–1525.CrossRefGoogle Scholar
Budisic, M., Mohr, R. & Mezic, I. 2012 Applied Koopmanism. Chaos 22, 047510.Google Scholar
Candel, S. M. 1992 Combustion instabilities coupled by pressure waves and their active control. Proc. Combust. Inst. 24 (1), 1277–1296.CrossRefGoogle Scholar
Candel, S. M., Durox, D., Ducruix, S., Birbaud, A. L., Noiray, N. & Schuller, T. 2009 Flame dynamics and combustion noise: progress and challenges. Intl J. Aeroacoust. 8 (1), 1–56.CrossRefGoogle Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.Google Scholar
Chigier, N. A. & Beér, J. M. 1964 Velocity and static-pressure distributions in swirling air jets issuing from annular and divergent nozzles. Trans. ASME J. Basic Engng 86 (4), 788–796.Google Scholar
Cho, J. H. & Lieuwen, T. 2005 Laminar premixed flame response to equivalence ratio oscillations. Combust. Flame 140 (1–2), 116–129.Google Scholar
Chomaz, J. M., Huerre, P. & Redekopp, L. G. 1991 A frequency selection criterion in spatially developing flows. Stud. Appl. Maths 84, 119–144.CrossRefGoogle Scholar
Chterev, I., Foley, C. W., Foti, D., Kostka, S., Caswell, A. W., Jiang, N., Lynch, A., Noble, D. R., Menon, S., Seitzman, J. M. et al. 2014 Flame and flow topologies in an annular swirling flow. Combust. Sci. Technol. 186, 1041–1074.Google Scholar
Cohen, J. M. & Rosfjord, T. J. 1993 Influences on the sprays formed by high-shear fuel nozzle/swirler assemblies. J. Propul. Power 9 (1), 16–27.Google Scholar
Culick, F. E. C.2006 Unsteady motions in combustion chambers for propulsion systems. RTO AGARDograph AG-AVT-039, North Atlantic Treaty Organization.Google Scholar
Dowling, A. P. 1999 A kinematic model of a ducted flame. J. Fluid Mech. 394, 51–72.Google Scholar
Dowling, A. P. & Stow, S. R. 2003 Acoustic analysis of gas turbine combustors. J. Propul. Power 19 (5), 751–764.Google Scholar
Drake, M. C., Pitz, R. W., Lapp, M., Fenimore, C. P., Lucht, R. P., Sweeney, D. W. & Laurendeau, N. M. 1984 Measurements of superequilibrium hydroxyl concentrations in turbulent nonpremixed flames using staturated fluorescence. Proc. Combust. Inst. 20 (1), 327–335.CrossRefGoogle Scholar
Ducruix, S., Schuller, T., Durox, D. & Candel, S. M. 2003 Combustion dynamics and instabilities: elementary coupling and driving mechanisms. J. Propul. Power 19 (5), 722–734.CrossRefGoogle Scholar
Duran, I., Moreau, S. & Poinsot, T. 2013 Analytical and numerical study of combustion noise through a subsonic nozzle. AIAA J. 51 (1), 42–52.CrossRefGoogle Scholar
Duwig, C. & Fuchs, L. 2007 Large eddy simulation of vortex breakdown/flame interactions. Phys. Fluids 19, 075103.Google Scholar
Emara, A., Lacarelle, A. & Paschereit, C. 2009 Planar investigation of outlet boundary conditions effect on isothermal flow fields of a swirl-stabilized burner. In ASME Turbo Expo Power for Land, Sea, and Air, Volume 2: Combustion, Fuels and Emissions, Orlando, FL, USA, 8–12 June, 2009. GT2009-59948.Google Scholar
Escudier, M. 1988 Vortex breakdown: observations and explanation. Prog. Aerosp. Sci. 25 (2), 189–229.CrossRefGoogle Scholar
Feng, C., Liu, F., Rusak, Z. & Wang, S.2016 Flow simulation of the dynamics of a perturbed solid-body rotation flow. AIAA Paper 2016–4388.CrossRefGoogle Scholar
Fleifil, M., Annaswamy, A. M., Ghoniem, Z. A. & Ghoniem, A. F. 1996 Response of a laminar premixed flame to flow oscillations: a kinematic model and thermoacoustic instability results. Combust. Flame 106 (4), 487–510.Google Scholar
Gallaire, F. & Chomaz, J.-M. 2003 Instability mechanisms in swirling flows. Phys. Fluids 15 (9), 2622–2639.Google Scholar
Garcia-Villalba, M., Frohlich, J. & Rodi, W. 2006 Identification and analysis of coherent structures in the near field of a turbulent unconfined annular swirling jet using large eddy simulation. Phys. Fluids 18, 055103.CrossRefGoogle Scholar
Giovangigli, V. & Smooke, M. D. 1987 Extinction of strained premixed laminar flames with complex chemistry. Combust. Sci. Technol. 53 (1), 23–49.CrossRefGoogle Scholar
Gupta, A. K., Lilley, D. J. & Syred, N. 1984 Swirl Flows. Abacus Press.Google Scholar
Hall, M. G. 1972 Vortex breakdown. Annu. Rev. Fluid Mech. 4, 195–218.Google Scholar
Ho, C. M. & Huerre, P. 1984 Perturbed free shear layers. Annu. Rev. Fluid Mech. 16, 365–422.Google Scholar
Holmes, P., Lumley, J. L. & Berkooz, G. 1996 Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.CrossRefGoogle Scholar
Huang, Y. & Yang, V. 2009 Dynamics and stability of lean-premixed swirl-stabilized combustion. Prog. Energy Combust. Sci. 35 (4), 293–364.Google Scholar
Huerre, P. & Monkewitz, P. A. 1985 Absolute and convective instabilities in free shear layers. J. Fluid Mech. 159, 151–168.Google Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.Google Scholar
Ju, Y., Guo, H., Maruta, K. & Liu, F. 1997 On the extinction limit and flammability limit of non-adiabatic stretched methane–air premixed flames. J. Fluid Mech. 342, 315–334.Google Scholar
Kiesewetter, F., Konle, M. & Sattelmayer, T. 2007 Analysis of combustion induced vortex breakdown driven flame flashback in a premix burner with cylindrical mixing zone. Trans. ASME J. Engng Gas Turbines Power 129, 929–936.Google Scholar
Kostka, S., Lynch, A. C., Huelskamp, B. C., Kiel, B. V., Gord, J. R. & Roy, S. 2012 Characterization of flame-shedding behavior behind a bluff-body using proper orthogonal decomposition. Combust. Flame 159 (9), 2872–2882.Google Scholar
Law, C. K. 2006 Combustion Physics. Cambridge University Press.Google Scholar
Leibovich, S. 1984 Vortex stability and breakdown: survey and extension. AIAA J. 22 (9), 1192–1206.CrossRefGoogle Scholar
Lieuwen, T. & Yang, V.(Eds) 2005 Combustion Instabilities in Gas Turbine Engines: Operational Experience, Fundamental Mechanisms, and Modeling, Progress in Astronautics and Aeronautics, vol. 210. American Institute of Aeronautics and Astronautics.Google Scholar
Lieuwen, T. & Zinn, B. T. 1998 The role of equivalence ratio oscillations in driving combustion instabilities in low NO x gas turbines. Proc. Combust. Inst. 27 (2), 1809–1816.CrossRefGoogle Scholar
Lieuwen, T. C. 2012 Unsteady Combustor Physics. Cambridge University Press.Google Scholar
Loiseleux, T. C., Chomaz, J. M. & Huerre, P. 1998 The effect of swirl on jets and wakes: linear instability of the Rankine vortex with axial flow. Phys. Fluids 10 (5), 1120–1134.Google Scholar
Lucca-Negro, O. & O’Doherty, T. 2001 Vortex breakdown: a review. Prog. Energy Combust. Sci. 27, 431–481.Google Scholar
Marble, F. E. & Candel, S. M. 1977 Acoustic disturbance from gas non-uniformities convected through a nozzle. J. Sound Vib. 55 (2), 225–243.Google Scholar
McManus, K. R., Pointsot, T. & Candel, S. M. 1993 A review of active control of combustion instabilities. Prog. Energy Combust. Sci. 19 (1), 1–29.Google Scholar
Meliga, P., Gallarire, F. & Chomaz, J.-M. 2012 A weakly nonlinear mechanism for mode selection in swirling jets. J. Fluid Mech. 699, 216–262.Google Scholar
Mezić, I. 2013 Analysis of fluid flows via spectral properties of the Koopman operator. Annu. Rev. Fluid Mech. 45, 357–378.CrossRefGoogle Scholar
Mezić, I. & Banaszuk, A. 2004 Comparison of systems with complex behavior. Physica D 197 (1–2), 101–133.Google Scholar
Moeck, J. P., Bourgouin, J.-F., Durox, D., Schuller, T. & Candel, S. M. 2012 Nonlinear interaction between a precessing vortex core and acoustic oscillations. Combust. Flame 159, 2650–2668.CrossRefGoogle Scholar
Nair, V. & Sujith, R. I. 2014 Multifractality in combustion noise: predicting an impending combustion instability. J. Fluid Mech. 747, 635–655.Google Scholar
Nair, V., Thampi, G. & Sujith, R. I. 2014 Intermittency route to thermoacoustic instability in turbulent combustors. J. Fluid Mech. 756, 470–487.Google Scholar
Oberleithner, K., Sieber, M., Nayeri, C. N., Paschereit, C. O., Petz, C., Hege, H. C., Noack, B. R. & Wygnanski, I. 2011 Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: stability analysis and empirical mode construction. J. Fluid Mech. 679, 383–414.CrossRefGoogle Scholar
Oberleithner, K., Stöhr, M., Im, H. S., Arndt, C. M. & Steinberg, A. M. 2015 Formation and flame-induced suppression of the precessing vortex core in a swirl combustor: experiments and linear stability analysis. Combust. Flame 162 (8), 3100–3114.Google Scholar
O’Connor, J., Acharya, V. & Lieuwen, T. 2015 Transverse combustion instabilities: acoustic, fluid mechanic, and flame processes. Prog. Energy Combust. Sci. 49, 1–39.Google Scholar
O’Connor, J. & Lieuwen, T. 2011 Disturbance field characteristics of a transversely excited burner. Combust. Sci. Technol. 183 (5), 427–443.CrossRefGoogle Scholar
Panda, P. P., Roa, M., Slabaugh, C. D., Peltier, S., Carter, C. D., Laster, W. R. & Lucht, R. P. 2016 High-repetition-rate planar measurements in the wake of a reacting jet injected into a swirling vitiated crossflow. Combust. Flame 163, 241–257.Google Scholar
Poinsot, T. J., Trouve, A. C., Veynante, D. P., Candel, S. M. & Esposito, E. J. 1987 Vortex-driven acoustically coupled combustion instabilities. J. Fluid Mech. 177, 265–292.Google Scholar
Ravindran, S. S. 2000 A reduced-order approach for optimal control of fluids using proper orthogonal decomposition. Intl. J. Numer. Meth. Engng 34, 425–448.3.0.CO;2-W>CrossRefGoogle Scholar
Rosenstein, M. T., Collins, J. J. & De Luca, C. J. 1993 A practical method for calculating largest Lyapunov exponents. Physica D 65, 117–134.Google Scholar
Roux, S., Lartigue, G., Poinsot, T., Meier, U. & Berat, C. 2005 Studies of mean and unsteady flow in a swirled combustor using experiments, acoustic analysis, and large eddy simulation. Combust. Flame 141, 40–54.Google Scholar
Rowley, C. W., Mezć, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.Google Scholar
Roy, S., Hua, J. C., Barnhill, W., Gunaratne, G. H. & Gord, J. R. 2015 Deconvolution of reacting-flow dynamics using proper orthogonal and dynamic mode decomposition. Phys. Rev. E 91, 013001.Google Scholar
Ruith, M. R., Chen, P., Meiburg, E. & Maxworthy, T. 2003 Three-dimensional vortex breakdown in swirling jets and wakes: direct numerical simulation. J. Fluid Mech. 486, 331–378.Google Scholar
Rukes, L., Sieber, M., Paschereit, C. O. & Oberleithner, K. 2015 Effect of initial vortex core size on the coherent structures in the swirling jet near field. Exp. Fluids 56, 197.CrossRefGoogle Scholar
Rusak, W. & Wang, S. 2014 Wall-separation and vortex-breakdown zones in a solid-body rotation flow in a rotating finite-length straight circular pipe. J. Fluid Mech. 759, 321–359.Google Scholar
Rusak, Z., Wang, S., Xu, L. & Taylor, S. 2012 On the global nonlinear stability of a near-critical swirling flow in a long finite-length pipe and the path to vortex breakdown. J. Fluid Mech. 712, 295–326.Google Scholar
Sadanandan, R., Stöhr, M. & Meier, W. 2008 Simultaneous OH-PLIF and PIV measurements in a gas turbine model combustor. Appl. Phys. B 90, 609–618.Google Scholar
Schadow, K. C. & Gutmark, E. 1992 Combustion instability related to vortex shedding in dump combustors and their passive control. Prog. Energy Combust. Sci. 18 (2), 117–132.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Selle, L., Benoit, L., Poinsot, T., Nicoud, F. & Krebs, W. 2006 Joint use of compressible large-eddy simulation and Helmholtz solver for the analysis of rotating modes in an industrial swirled burner. Combust. Flame 145, 194–205.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Parts I–III: coherent structures. Q. Appl. Maths 45 (3), 561–590.Google Scholar
Steinberg, A. M., Boxx, I., Stöhr, M., Carter, C. D. & Meier, W. 2010 Flow–flame interactions causing acoustically coupled heat release fluctuations in a thermo-acoustically unstable gas turbine model combustor. Combust. Flame 157 (12), 2250–2266.CrossRefGoogle Scholar
Stöhr, M., Arndt, C. M. & Meier, W. 2013 Effects of Damköhler number on vortex–flame interaction in a gas turbine model combustor. Proc. Combust. Inst. 34 (2), 3107–3115.Google Scholar
Stöhr, M., Boxx, I., Carter, C. D. & Meier, W. 2012 Experimental study of vortex–flame interaction in a gas turbine model combustor. Combust. Flame 159, 2636–2649.Google Scholar
Stöhr, M, Sadanandan, R. & Meier, W. 2011 Phase-resolved characterization of vortex–flame interaction in a turbulent swirl flame. Exp. Fluids 51, 1153–1167.Google Scholar
Syred, N. 2006 A review of oscillation mechanisms and the role of the precessing vortex core (PVC) in swirl combustion systems. Prog. Energy Combust. Sci. 32, 93–161.CrossRefGoogle Scholar
Syred, N. & Beer, J. M. 1974 Combustion in swirling flows: a review. Combust. Flame 23 (2), 143–201.Google Scholar
Tu, J. H., Rowley, C. W., Luchtenburg, D. M., Brunton, S. L. & Kutz, J. N. 2014 On dynamic mode decomposition: theory and applications. J. Comput. Dyn. 1 (2), 391–421.Google Scholar
Umeh, C. O. U., Rusak, Z. & Gutmark, E. 2012 Vortex breakdown in a swirl-stabilized combustor. J. Propul. Power 28 (5), 1037–1051.Google Scholar
Valera-Medina, A., Syred, N. & Griffiths, A. 2009 Visualization of isothermal large coherent structures in a swirl burner. Combust. Flame 156, 1723–1734.Google Scholar
Wang, S. & Rusak, Z. 1996 On the stability of axisymmetric swirling flows. Phys. Fluids 8 (4), 1007–1016.CrossRefGoogle Scholar
Wang, S. & Rusak, Z. 1997 The dynamics of a swirling flow in a pipe and transition to axisymmetric vortex breakdown. J. Fluid Mech. 340, 177–223.Google Scholar
Wang, S., Rusak, Z., Gong, R. & Liu, F. 2016 On the three-dimensional stability of a solid-body rotation flow in a finite-length rotating pipe. J. Fluid Mech. 797, 284–321.Google Scholar
Wang, S., Yang, V., Hsiao, G., Hsieh, S. Y. & Mongia, H. C. 2007 Large-eddy simulations of gas-turbine swirl injector flow dynamics. J. Fluid Mech. 583, 99–122.Google Scholar
Wee, D., Yi, T., Annaswamy, A. M. & Ghoniem, A. F. 2004 Self-sustained oscillations and vortex shedding in backward-facing step flows: simulation and linear instability analysis. Phys. Fluids 16, 3361–3373.Google Scholar
Wolf, A., Swift, J. B., Swinney, H. L. & Vastano, J. A. 1985 Determining Lyapunov exponents from a time series. Physica D 16 (3), 285–317.Google Scholar
Yang, V.(Ed.) 1995 Liquid Rocket Engine Combustion Instability, Progress in Astronautics and Aeronautics, vol. 169. American Institute of Aeronautics and Astronautics.Google Scholar
Yi, T. & Gutmark, E. J. 2007 Real-time prediction of incipient lean blowout in gas turbine combustors. AIAA J. 45 (7), 1734–1739.Google Scholar
Yi, T. & Santavicca, D. A. 2009a Flame spectra for turbulent liquid-fueled swirl-stabilized LDI combustion. J. Propul. Power 25 (5), 1058–1067.Google Scholar
Yi, T. & Santavicca, D. A. 2009b Forced flame response of turbulent liquid-fueled swirl-stabilized LDI combustion to fuel modulations. J. Propul. Power 25 (6), 1259–1271.CrossRefGoogle Scholar
Yi, T & Santavicca, D. A. 2012 Combustion instability and flame structure of turbulent swirl-stabilized liquid-fueled combustion. J. Propul. Power 28 (5), 1000–1014.Google Scholar
Yi, T., Wee, D., Annaswamy, A. M. & Ghiniem, A. F. 2003 Self-sustained oscillations in separating flows I: stability analysis and reduced-order modeling; II: reduced-order modeling and control. In Proceedings of the International Colloquium on Combustion Noise and Control, pp. 214–227.Google Scholar