Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-04T09:18:07.125Z Has data issue: false hasContentIssue false
  • English
  • Français

The energy cascade in near-field non-homogeneous non-isotropic turbulence

Published online by Cambridge University Press:  23 April 2015

R. Gomes-Fernandes ,
B. Ganapathisubramani  and
J. C. Vassilicos
R. Gomes-Fernandes
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
B. Ganapathisubramani
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, Southampton SO17 1BJ, UK
J. C. Vassilicos*
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: j.c.vassilicos@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We perform particle image velocimetry (PIV) measurements of various terms of the non-homogeneous Kármán–Howarth–Monin equation in the most inhomogeneous and anisotropic region of grid-generated turbulence, the production region which lies between the grid and the peak of turbulence intensity. We use a well-documented fractal grid which is known to magnify the streamwise extent of the production region and abate its turbulence activity. On the centreline around the centre of that region the two-point advection and transport terms are dominant and the production is significant too. It is therefore impossible to apply usual Kolmogorov arguments based on the Kármán–Howarth–Monin equation and resulting dimensional considerations to deduce interscale flux and spectral properties. The interscale energy transfers at this location turn out to be highly anisotropic and consist of a combined forward and inverse cascade in different directions which, when averaged over directions, gives an interscale energy flux that is negative (hence forward cascade on average) and not too far from linear in $r$, the modulus of the separation vector $\boldsymbol{r}$ between two points. The energy spectrum of the streamwise fluctuating component exhibits a well-defined 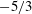$-5/3$ power law over one decade, even though the streamwise direction is at a small angle to the inverse cascading direction.

JFM classification

Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 771 , 25 May 2015 , pp. 676 - 705
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Braza, M., Perrin, R. & Hoarau, Y. 2006 Turbulence properties in the cylinder wake at high Reynolds numbers. J. Fluids Struct. 22 (6), 757–771.CrossRefGoogle Scholar
Danaila, L., Krawczynski, J. F., Thiesset, F. & Renou, B. 2012 Yaglom-like equation in axisymmetric anisotropic turbulence. Physica D 241 (3), 216–223.CrossRefGoogle Scholar
Deissler, R. G. 1961 Effects of inhomogeneity and of shear flow in weak turbulent fields. Phys. Fluids 4 (10), 1187–1198.CrossRefGoogle Scholar
Discetti, S., Ziskin, I. B., Astarita, T., Adrian, R. J. & Prestridge, K. P. 2013 PIV measurements of anisotropy and inhomogeneity in decaying fractal generated turbulence. Fluid Dyn. Res. 45 (6), 061401.CrossRefGoogle Scholar
Dong, S., Karniadakis, G. E., Ekmekci, A. & Rockwell, D. 2006 A combined direct numerical simulation–particle image velocimetry study of the turbulent near wake. J. Fluid Mech. 569 (1), 185–207.CrossRefGoogle Scholar
Ganapathisubramani, B., Lakshminarasimhan, K. & Clemens, N. T. 2007 Determination of complete velocity gradient tensor by using cinematographic stereoscopic PIV in a turbulent jet. Exp. Fluids 42, 923–939.CrossRefGoogle Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2012 Particle image velocimetry study of fractal-generated turbulence. J. Fluid Mech. 711, 306–336.CrossRefGoogle Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2014 Evolution of the velocity-gradient tensor in a spatially developing turbulent flow. J. Fluid Mech. 756, 252–292.CrossRefGoogle Scholar
Hill, R. J. 2002 Exact second-order structure–function relationships. J. Fluid Mech. 468, 317–326.CrossRefGoogle Scholar
Hurst, D. & Vassilicos, J. C. 2007 Scalings and decay of fractal-generated turbulence. Phys. Fluids 19, 035103.CrossRefGoogle Scholar
Jayesh & Warhaft, Z. 1992 Probability distribution, conditional dissipation, and transport of passive temperature fluctuations in grid-generated turbulence. Phys. Fluids A 4, 2292–2307.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941a Dissipation of energy in locally isotropic turbulence. C. R. Acad Sci. SSSR 32, 16–18.Google Scholar
Kolmogorov, A. N. 1941b The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. C. R. Acad Sci. SSSR 30, 301–305.Google Scholar
Kolmogorov, A. N. 1941c On degeneration of isotropic turbulence in an incompressible viscous liquid. C. R. Acad Sci. SSSR 31, 538–540.Google Scholar
Laizet, S. & Vassilicos, J. C. 2011 DNS of fractal-generated turbulence. Flow Turbul. Combust. 87, 673–705.CrossRefGoogle Scholar
Laizet, S. & Vassilicos, J. C. 2012 Fractal space-scale unfolding mechanism for energy-efficient turbulent mixing. Phys. Rev. E 86 (4), 046302.CrossRefGoogle ScholarPubMed
Laizet, S. & Vassilicos, J. C. 2015 Stirring and scalar transfer by grid-generated turbulence in the presence of a mean scalar gradient. J. Fluid Mech. 764, 52–75.CrossRefGoogle Scholar
Laizet, S., Vassilicos, J. C. & Cambon, C. 2013 Interscale energy transfer in decaying turbulence and vorticity-strain rate dynamics in grid-generated turbulence. Fluid Dyn. Res. 45 (6), 061408.CrossRefGoogle Scholar
Lamriben, C., Cortet, P.-P. & Moisy, F. 2011 Direct measurements of anisotropic energy transfers in a rotating turbulence experiment. Phys. Rev. Lett. 107 (2), 024503.CrossRefGoogle Scholar
Marati, N., Casciola, C. M. & Piva, R. 2004 Energy cascade and spatial fluxes in wall turbulence. J. Fluid Mech. 521, 191–215.CrossRefGoogle Scholar
Mazellier, N. & Vassilicos, J. C. 2010 Turbulence without Richardson–Kolmogorov cascade. Phys. Fluids 22, 075101.CrossRefGoogle Scholar
Nagata, K., Sakai, Y., Suzuki, H., Suzuki, H., Terashima, O. & Inaba, T. 2013 Turbulence structure and turbulence kinetic energy transport in multiscale/fractal-generated turbulence. Phys. Fluids 25, 065102.CrossRefGoogle Scholar
Nie, Q. & Tanveer, S. 1999 A note on third-order structure functions in turbulence. Proc. R. Soc. Lond. A 455 (1985), 1615–1635.CrossRefGoogle Scholar
Richardson, L. F. 1922 Weather Prediction by Numerical Process. Cambridge University Press.Google Scholar
Seoud, R. E. & Vassilicos, J. C. 2007 Dissipation and decay of fractal-generated turbulence. Phys. Fluids 19, 105108.CrossRefGoogle Scholar
Soloff, S. M., Adrian, R. J. & Liu, Z.-C. 1997 Distortion compensation for generalized stereoscopic particle image velocimetry. Meas. Sci. Technol. 8, 1441–1454.CrossRefGoogle Scholar
Tanaka, T. & Eaton, J. K. 2007 A correction method for measuring turbulence kinetic energy dissipation rate by PIV. Exp. Fluids 42, 893–902.CrossRefGoogle Scholar
Valente, P. C. & Vassilicos, J. C. 2011 The decay of turbulence generated by a class of multi-scale grids. J. Fluid Mech. 687, 300–340.CrossRefGoogle Scholar
Valente, P. C. & Vassilicos, J. C. 2014 The non-equilibrium region of grid-generated decaying turbulence. J. Fluid Mech. 744, 5–37.CrossRefGoogle Scholar
Valente, P. C. & Vassilicos, J. C. 2015 The energy cascade in grid-generated non-equilibrium decaying turbulence. Phys. Fluids; Under review.CrossRefGoogle Scholar