Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Schmitt, R. W.
2012.
Finger puzzles.
Journal of Fluid Mechanics,
Vol. 692,
Issue. ,
p.
1.
Garaud, P.
Alecian, G.
Lebreton, Y.
Richard, O.
and
Vauclair, G.
2013.
Double-diffusive convection.
EAS Publications Series,
Vol. 63,
Issue. ,
p.
285.
Hewitt, Duncan R.
Neufeld, Jerome A.
and
Lister, John R.
2013.
Stability of columnar convection in a porous medium.
Journal of Fluid Mechanics,
Vol. 737,
Issue. ,
p.
205.
Brown, Justin M.
Garaud, Pascale
and
Stellmach, Stephan
2013.
CHEMICAL TRANSPORT AND SPONTANEOUS LAYER FORMATION IN FINGERING CONVECTION IN ASTROPHYSICS.
The Astrophysical Journal,
Vol. 768,
Issue. 1,
p.
34.
Flanagan, Jason D.
Radko, Timour
Shaw, William J.
and
Stanton, Timothy P.
2014.
Dynamic and Double-Diffusive Instabilities in a Weak Pycnocline. Part II: Direct Numerical Simulations and Flux Laws.
Journal of Physical Oceanography,
Vol. 44,
Issue. 8,
p.
1992.
Radko, T.
Bulters, A.
Flanagan, J. D.
and
Campin, J.-M.
2014.
Double-Diffusive Recipes. Part I: Large-Scale Dynamics of Thermohaline Staircases.
Journal of Physical Oceanography,
Vol. 44,
Issue. 5,
p.
1269.
Radko, Timour
2014.
Applicability and failure of the flux-gradient laws in double-diffusive convection.
Journal of Fluid Mechanics,
Vol. 750,
Issue. ,
p.
33.
Radko, T.
Flanagan, J. D.
Stellmach, S.
and
Timmermans, M.-L.
2014.
Double-Diffusive Recipes. Part II: Layer-Merging Events.
Journal of Physical Oceanography,
Vol. 44,
Issue. 5,
p.
1285.
Singh, O. P.
and
Srinivasan, J.
2014.
Effect of Rayleigh numbers on the evolution of double-diffusive salt fingers.
Physics of Fluids,
Vol. 26,
Issue. 6,
Radko, T.
Peixoto de Carvalho, D.
and
Flanagan, J.
2014.
Nonlinear Equilibration of Baroclinic Instability: The Growth Rate Balance Model.
Journal of Physical Oceanography,
Vol. 44,
Issue. 7,
p.
1919.
Radko, Timour
Ball, James
Colosi, John
and
Flanagan, Jason
2015.
Double-Diffusive Convection in a Stochastic Shear.
Journal of Physical Oceanography,
Vol. 45,
Issue. 12,
p.
3155.
Nagai, Takeyoshi
Inoue, Ryuichiro
Tandon, Amit
and
Yamazaki, Hidekatsu
2015.
Evidence of enhanced double‐diffusive convection below the main stream of the Kuroshio Extension.
Journal of Geophysical Research: Oceans,
Vol. 120,
Issue. 12,
p.
8402.
Garaud, Pascale
and
Brummell, Nicholas
2015.
2D OR NOT 2D: THE EFFECT OF DIMENSIONALITY ON THE DYNAMICS OF FINGERING CONVECTION AT LOW PRANDTL NUMBER.
The Astrophysical Journal,
Vol. 815,
Issue. 1,
p.
42.
Liu, Li
and
Zikanov, Oleg
2015.
Elevator mode convection in flows with strong magnetic fields.
Physics of Fluids,
Vol. 27,
Issue. 4,
Garaud, P.
Medrano, M.
Brown, J. M.
Mankovich, C.
and
Moore, K.
2015.
EXCITATION OF GRAVITY WAVES BY FINGERING CONVECTION, AND THE FORMATION OF COMPOSITIONAL STAIRCASES IN STELLAR INTERIORS.
The Astrophysical Journal,
Vol. 808,
Issue. 1,
p.
89.
Yang, Yantao
van der Poel, Erwin P.
Ostilla-Mónico, Rodolfo
Sun, Chao
Verzicco, Roberto
Grossmann, Siegfried
and
Lohse, Detlef
2015.
Salinity transfer in bounded double diffusive convection.
Journal of Fluid Mechanics,
Vol. 768,
Issue. ,
p.
476.
Radko, Timour
and
Edwards, Erick
2016.
Diapycnal Velocity in the Double-Diffusive Thermocline.
Fluids,
Vol. 1,
Issue. 3,
p.
25.
Yang, Yantao
Verzicco, Roberto
and
Lohse, Detlef
2016.
Scaling laws and flow structures of double diffusive convection in the finger regime.
Journal of Fluid Mechanics,
Vol. 802,
Issue. ,
p.
667.
Falco, Pierpaolo
Trani, Marilisa
and
Zambianchi, Enrico
2016.
Water mass structure and deep mixing processes in the Tyrrhenian Sea: Results from the VECTOR project.
Deep Sea Research Part I: Oceanographic Research Papers,
Vol. 113,
Issue. ,
p.
7.
Radko, Timour
and
Sisti, Cassandra
2017.
Life and Demise of Intrathermocline Mesoscale Vortices.
Journal of Physical Oceanography,
Vol. 47,
Issue. 12,
p.
3087.
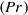 and decreasing with diffusivity ratio
and decreasing with diffusivity ratio 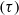 . Theory is successfully tested by a series of direct numerical simulations which span a wide range of
. Theory is successfully tested by a series of direct numerical simulations which span a wide range of 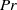 and
and  .
.
