Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-18T04:26:04.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Evolution of thermally stratified turbulent open channel flow after removal of the heat source

Published online by Cambridge University Press:  01 August 2019

Michael P. Kirkpatrick Open the ORCID record for Michael P. Kirkpatrick [Opens in a new window] ,
N. Williamson Open the ORCID record for N. Williamson [Opens in a new window] ,
S. W. Armfield  and
V. Zecevic
Michael P. Kirkpatrick*
Affiliation:
School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, Sydney, NSW2006, Australia
N. Williamson
Affiliation:
School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, Sydney, NSW2006, Australia
S. W. Armfield
Affiliation:
School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, Sydney, NSW2006, Australia
V. Zecevic
Affiliation:
School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, Sydney, NSW2006, Australia
*
†Email address for correspondence: michael.kirkpatrick@sydney.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

Evolution of thermally stratified open channel flow after removal of a volumetric heat source is investigated using direct numerical simulation. The heat source models radiative heating from above and varies with height due to progressive absorption. After removal of the heat source the initial stable stratification breaks down and the channel approaches a fully mixed isothermal state. The initial state consists of three distinct regions: a near-wall region where stratification plays only a minor role, a central region where stratification has a significant effect on flow dynamics and a near-surface region where buoyancy effects dominate. We find that a state of local energetic equilibrium observed in the central region of the channel in the initial state persists until the late stages of the destratification process. In this region local turbulence parameters such as eddy diffusivity 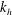$k_{h}$ and flux Richardson number 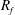$R_{f}$ are found to be functions only of the Prandtl number 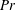$Pr$ and a mixed parameter 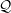${\mathcal{Q}}$, which is equal to the ratio of the local buoyancy Reynolds number 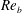$Re_{b}$ and the friction Reynolds number 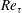$Re_{\unicode[STIX]{x1D70F}}$. Close to the top and bottom boundaries turbulence is also affected by 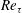$Re_{\unicode[STIX]{x1D70F}}$ and vertical position $z$. In the initial heated equilibrium state the laminar surface layer is stabilised by the heat source, which acts as a potential energy sink. Removal of the heat source allows Kelvin–Helmholtz-like shear instabilities to form that lead to a rapid transition to turbulence and significantly enhance the mixing process. The destratifying flow is found to be governed by bulk parameters 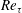$Re_{\unicode[STIX]{x1D70F}}$, 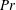$Pr$ and the friction Richardson number 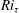$Ri_{\unicode[STIX]{x1D70F}}$. The overall destratification rate 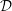${\mathcal{D}}$ is found to be a function of 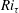$Ri_{\unicode[STIX]{x1D70F}}$ and 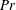$Pr$.

JFM classification

Geophysical and Geological Flows: River dynamics Geophysical and Geological Flows: Stratified flows Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 876 , 10 October 2019 , pp. 356 - 412
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bell, J. B., Colella, P. & Glaz, H. M. 1989 A second-order projection method for the incompressible Navier–Stokes equations. J. Comput. Phys. 85 (2), 257–283.Google Scholar
Bluteau, C. E., Jones, N. L. & Ivey, G. N. 2013 Turbulent mixing efficiency at an energetic ocean site. J. Geophys. Res. 118 (9), 4662–4672.Google Scholar
Bormans, M., Ford, P. W. & Fabbro, L. 2005 Spatial and temporal variability in cyanobacterial populations controlled by physical processes. J. Plankton Res. 27 (1), 61–70.Google Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.Google Scholar
Britter, R. E.1974 An experiment on turbulence in a density stratified fluid. PhD thesis, Monash University, Victoria, Australia.Google Scholar
Brucker, K. A. & Sarkar, S. 2007 Evolution of an initially turbulent stratified shear layer. Phys. Fluids 19 (10), 105105.Google Scholar
Calmet, I. & Magnaudet, J. 2003 Statistical structure of high-Reynolds-number turbulence close to the free surface of an open-channel flow. J. Fluid Mech. 474, 355–378.Google Scholar
Caulfield, C. P. & Peltier, W. R. 2000 The anatomy of the mixing transition in homogeneous and stratified free shear layers. J. Fluid Mech. 413, 1–47.Google Scholar
Chung, D. & Matheou, G. 2012 Direct numerical simulation of stationary homogeneous stratified sheared turbulence. J. Fluid Mech. 696, 434–467.Google Scholar
Deusebio, E., Caulfield, C. P. & Taylor, J. R. 2015 The intermittency boundary in stratified plane Couette flow. J. Fluid Mech. 781, 298–329.Google Scholar
Dyer, A. J. 1974 A review of flux-profile relationships. Boundary-Layer Meteorol. 7 (3), 363–372.Google Scholar
Ellison, T. H. 1957 Turbulent transport of heat and momentum from an infinite rough plane. J. Fluid Mech. 2 (5), 456–466.Google Scholar
Flores, O. & Riley, J. J. 2011 Analysis of turbulence collapse in the stably stratified surface layer using direct numerical simulation. Boundary-Layer Meteorol. 139 (2), 241–259.Google Scholar
Foken, T. 2006 50 years of the Monin–Obukhov similarity theory. Boundary-Layer Meteorol. 119 (3), 431–447.Google Scholar
Garcia-Villalba, M. & del Alamo, J. C. 2011 Turbulence modification by stable stratification in channel flow. Phys. Fluids 23 (4), 045104.Google Scholar
Garg, R. P., Ferziger, J. H., Monismith, S. G. & Koseff, J. R. 2000 Stably stratified turbulent channel flows. I. Stratification regimes and turbulence suppression mechanism. Phys. Fluids 12 (10), 2569–2594.Google Scholar
Gargett, A. E., Osborn, T. R. & Nasmyth, P. W. 1984 Local isotropy and the decay of turbulence in a stratified fluid. J. Fluid Mech. 144, 231–281.Google Scholar
Hokpunna, A. & Manhart, M. 2010 Compact fourth-order finite volume method for numerical solutions of Navier–Stokes equations on staggered grids. J. Comput. Phys. 229 (20), 7545–7570.Google Scholar
Howland, C. J., Taylor, J. R. & Caulfield, C. P. 2018 Testing linear marginal stability in stratified shear layers. J. Fluid Mech. 839.Google Scholar
Hunt, J. C. R. & Graham, J. M. R. 1978 Free-stream turbulence near plane boundaries. J. Fluid Mech. 84 (2), 209–235.Google Scholar
Ivey, G. N., Bluteau, C. E. & Jones, N. L. 2018 Quantifying diapycnal mixing in an energetic ocean. J. Geophys. Res. 123 (1), 346–357.Google Scholar
Ivey, G. N. & Imberger, J. 1991 On the nature of turbulence in a stratified fluid. Part I: The energetics of mixing. J. Phys. Oceanogr. 21 (5), 650–658.Google Scholar
Ivey, G. N., Winters, K. B. & Koseff, J. R. 2008 Density stratification, turbulence, but how much mixing? Annu. Rev. Fluid Mech. 40 (1), 169–184.Google Scholar
Kaminski, A. K., Caulfield, C. P. & Taylor, J. R. 2017 Nonlinear evolution of linear optimal perturbations of strongly stratified shear layers. J. Fluid Mech. 825, 213–244.Google Scholar
Kaminski, A. K. & Smyth, W. D. 2019 Stratified shear instability in a field of pre-existing turbulence. J. Fluid Mech. 862, 639–658.Google Scholar
van Kan, J. 1986 A second-order accurate pressure-correction scheme for viscous incompressible flow. SIAM J. Sci. Stat. Comput. 7 (3), 870–891.Google Scholar
Kim, J. & Moin, P. 1989 Transport of passive scalars in a turbulent channel flow. In Turbulent Shear Flows 6 (ed. Andr, J.-C., Cousteix, J., Durst, F., Launder, B. E., Schmidt, F. W. & Whitelaw, J. H.), pp. 85–96. Springer.Google Scholar
Kirkpatrick, M. P.2002 A large eddy simulation code for industrial and environmental flows. PhD thesis, University of Sydney.Google Scholar
Lorenz, E. N. 1955 Available potential energy and the maintenance of the general circulation. Tellus 7 (2), 157–167.Google Scholar
Mater, B. D. & Venayagamoorthy, S. K. 2014a The quest for an unambiguous parameterization of mixing efficiency in stably stratified geophysical flows. Geophys. Res. Lett. 41 (13), 4646–4653.Google Scholar
Mater, B. D. & Venayagamoorthy, S. K. 2014b A unifying framework for parameterizing stably stratified shear-flow turbulence. Phys. Fluids 26 (3), 036601.Google Scholar
Monin, A. S. 1970 The atmospheric boundary layer. Annu. Rev. Fluid Mech. 2 (1), 225–250.Google Scholar
Nieuwstadt, F. T. M. 1984 The turbulent structure of the stable, nocturnal boundary layer. J. Atmos. Sci. 41 (14), 2202–2216.Google Scholar
Osborn, T. R. 1980 Estimates of the local state of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10 (1), 83–89.Google Scholar
Osborn, T. R. & Cox, C. S. 1972 Oceanic fine structure. Geophys. Fluid Dyn. 3 (1), 321–345.Google Scholar
Salehipour, H. & Peltier, W. R. 2015 Diapycnal diffusivity, turbulent Prandtl number and mixing efficiency in Boussinesq stratified turbulence. J. Fluid Mech. 775, 464–500.Google Scholar
Scotti, A. & White, B. 2016 The mixing efficiency of stratified turbulent boundary layers. J. Phys. Oceanogr. 46 (10), 3181–3191.Google Scholar
Sherman, B. S., Webster, I. T., Jones, G. J. & Oliver, R. L. 1998 Transitions between Auhcoseira and Anabaena dominance in a turbid river weir pool. Limnol. Oceanogr. 43, 1902–1915.Google Scholar
Shih, L. H., Koseff, J. R., Ferziger, J. H. & Rehmann, C. R. 2000 Scaling and parameterization of stratified homogeneous turbulent shear flow. J. Fluid Mech. 412, 1–20.Google Scholar
Shih, L. H., Koseff, J. R., Ivey, G. N. & Ferziger, J. H. 2005 Parameterization of turbulent fluxes and scales using homogeneous sheared stably stratified turbulence simulations. J. Fluid Mech. 525, 193–214.Google Scholar
Smyth, W. D. & Moum, J. N. 2000 Length scales of turbulence in stably stratified mixing layers. Phys. Fluids 12 (6), 1327–1342.Google Scholar
Taylor, J. R., Sarkar, S. & Armenio, V. 2005 Large eddy simulation of stably stratified open channel flow. Phys. Fluids 17 (11), 116602.Google Scholar
Turner, L. & Erskine, W. D. 2005 Variability in the development, persistence and breakdown of thermal, oxygen and salt stratification on regulated rivers of southeastern Australia. River Res. Appl. 21, 151–168.Google Scholar
Van Buren, T., Williams, O. & Smits, A. J. 2017 Turbulent boundary layer response to the introduction of stable stratification. J. Fluid Mech. 811, 569–581.Google Scholar
Venayagamoorthy, S. K. & Koseff, J. R. 2016 On the flux Richardson number in stably stratified turbulence. J. Fluid Mech. 798, R1.Google Scholar
Walter, R. K., Squibb, M. E., Woodson, C. B., Koseff, J. R. & Monismith, S. G. 2014 Stratified turbulence in the nearshore coastal ocean: dynamics and evolution in the presence of internal bores. J. Geophys. Res. 119 (12), 8709–8730.Google Scholar
Webster, I. T., Sherman, B. S., Bormans, M. & Jones, G. 2000 Management strategies for cyanobacterial blooms in an impounded lowland river. Regul. Rivers: Res. Manage. 16 (5), 513–525.Google Scholar
Williamson, N., Armfield, S. W., Kirkpatrick, M. P. & Norris, S. E. 2015 Transition to stably stratified states in open channel flow with radiative surface heating. J. Fluid Mech. 766, 528–555.Google Scholar
Winters, K. B. & D’Asaro, E. A. 1996 Diascalar flux and the rate of fluid mixing. J. Fluid Mech. 317, 179–193.Google Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar
Zhou, Q., Taylor, J. R. & Caulfield, C. P. 2017 Self-similar mixing in stratified plane Couette flow for varying Prandtl number. J. Fluid Mech. 820, 86–120.Google Scholar