Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-23T11:39:22.394Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact coherent states with hairpin-like vortex structure in channel flow

Published online by Cambridge University Press:  15 June 2018

Ashwin Shekar  and
Michael D. Graham Open the ORCID record for Michael D. Graham [Opens in a new window]
Ashwin Shekar
Affiliation:
Department of Chemical and Biological Engineering, University of Wisconsin-Madison, Madison, WI 53706, USA
Michael D. Graham*
Affiliation:
Department of Chemical and Biological Engineering, University of Wisconsin-Madison, Madison, WI 53706, USA Kavli Institute for Theoretical Physics, University of California, Santa Barbara, CA 93106, USA
*
†Email address for correspondence: mdgraham@wisc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Hairpin vortices are widely studied as an important structural aspect of wall turbulence. The present work describes, for the first time, nonlinear travelling wave solutions to the Navier–Stokes equations in the channel flow geometry – exact coherent states (ECS) – that display hairpin-like vortex structure. 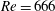This solution family comes into existence at a saddle-node bifurcation at Reynolds number $Re=666$. At the bifurcation, the solution has a highly symmetric quasi-streamwise vortex structure similar to that reported for previously studied ECS. With increasing distance from the bifurcation, however, both the upper and lower branch solutions develop a vortical structure characteristic of hairpins: a spanwise-oriented ‘head’ near the channel centreplane where the mean shear vanishes connected to counter-rotating quasi-streamwise ‘legs’ that extend toward the channel wall. At 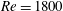$Re=1800$, the upper branch solution has mean and Reynolds shear-stress profiles that closely resemble those of turbulent mean profiles in the same domain.

JFM classification

Boundary Layers: Boundary layer structure Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , pp. 76 - 89
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.Google Scholar
Brand, E. & Gibson, J. F. 2014 A doubly-localized equilibrium solution of plane Couette flow. J. Fluid Mech. 750, R3.Google Scholar
Chantry, M., Willis, A. P. & Kerswell, R. R. 2014 Genesis of streamwise-localized solutions from globally periodic traveling waves in pipe flow. Phys. Rev. Lett. 112 (16), 164501.Google Scholar
Cherubini, S., Palma, P. D., Robinet, J. C. & Bottaro, A. 2011 Edge states in a boundary layer. Phys. Fluids 23 (5), 051705.Google Scholar
Duguet, Y., Pringle, C. C. T. & Kerswell, R. R. 2008a Relative periodic orbits in transitional pipe flow. Phys. Fluids 20 (11), 114102.Google Scholar
Duguet, Y., Schlatter, P., Henningson, D. S. & Eckhardt, B. 2012 Self-sustained localized structures in a boundary-layer flow. Phys. Rev. Lett. 108, 044501.Google Scholar
Duguet, Y., Willis, A. P. & Kerswell, R. R. 2008b Transition in pipe flow: the saddle structure on the boundary of turbulence. J. Fluid Mech. 613, 255–274.Google Scholar
Eckhardt, B., Faisst, H., Schmiegel, A. & Schneider, T. M. 2008 Dynamical systems and the transition to turbulence in linearly stable shear flows. Phil. Trans. R. Soc. Lond. A 366 (1868), 1297–1315.Google Scholar
Eckhardt, B., Schneider, T. M., Hof, B. & Westerweel, J. 2007 Turbulence transition in pipe flow. Annu. Rev. Fluid Mech. 39, 447–468.Google Scholar
Eitel-Amor, G., Örlü, R., Schlatter, P. & Flores, O. 2015 Hairpin vortices in turbulent boundary layers. Phys. Fluids 27 (2), 025108.Google Scholar
Gibson, J. F.2012 ChannelFlow: a spectral Navier–Stokes simulator in C $++$ . Tech. Rep., University of New Hampshire.Google Scholar
Gibson, J. F. & Brand, E. 2014 Spanwise-localized solutions of planar shear flows. J. Fluid Mech. 745, 25–61.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanović, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.Google Scholar
Hof, B., van Doorne, C. W., Westerweel, J., Nieuwstadt, F. T., Faisst, H., Eckhardt, B., Wedin, H., Kerswell, R. R. & Waleffe, F. 2004 Experimental observation of nonlinear traveling waves in turbulent pipe flow. Science 305 (5690), 1594–1598.Google Scholar
Itano, T. & Generalis, S. 2009 Hairpin vortex solution in planar couette flow: a tapestry of knotted vortices. Phys. Rev. Lett. 102, 114501.Google Scholar
Kawahara, G., Uhlmann, M. & van Veen, L. 2012 The significance of simple invariant solutions in turbulent flows. Annu. Rev. Fluid Mech. 44, 203–225.Google Scholar
Khapko, T., Kreilos, T., Schlatter, P., Duguet, Y., Eckhardt, B. & Henningson, D. S. 2013 Localized edge states in the asymptotic suction boundary layer. J. Fluid Mech. 717, R6.Google Scholar
Nagata, M. & Deguchi, K. 2013 Mirror-symmetric exact coherent states in plane Poiseuille flow. J. Fluid Mech. 735, R4.Google Scholar
Neelavara, S. A., Duguet, Y. & Lusseyran, F. 2017 State space analysis of minimal channel flow. Fluid Dyn. Res. 49 (3), 035511–16.Google Scholar
Park, J. S. & Graham, M. D. 2015 Exact coherent states and connections to turbulent dynamics in minimal channel flow. J. Fluid Mech. 782, 430–454.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 106–121.Google Scholar
Rawat, S., Cossu, C. & Rincon, F. 2016 Travelling-wave solutions bifurcating from relative periodic orbits in plane Poiseuille flow. Comptes Rendus Mécanique 344 (6), 448–455.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary-layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.Google Scholar
Schlatter, P., Li, Q., Örlü, R., Hussain, F. & Henningson, D. S. 2014 On the near-wall vortical structures at moderate Reynolds numbers. Eur. J. Mech. (B/Fluids) 48, 75–93.Google Scholar
Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96 (17), 174101.Google Scholar
Smits, A. J., Mckeon, B. J. & Marusic, I. 2011 High–Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43 (1), 353–375.Google Scholar
Theodorsen, T. 1952 Mechanism of Turbulence. In Second International Midwest Conference on Fluid Mechanics, pp. 1–19. Ohio State University.Google Scholar
Toh, S. & Itano, T. 2003 A periodic-like solution in channel flow. J. Fluid Mech. 481, 67–76.Google Scholar
Townsend, A. A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 11 (1), 97–120.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9 (4), 883–900.Google Scholar
Waleffe, F. 1998 Three-dimensional coherent states in plane shear flows. Phys. Rev. Lett. 81 (19), 4140–4143.Google Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.Google Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15 (6), 1517–1534.Google Scholar
Wall, D. P. & Nagata, M. 2016 Exact coherent states in channel flow. J. Fluid Mech. 788, 444–468.Google Scholar
Wang, J., Gibson, J. & Waleffe, F. 2007 Lower branch coherent states in shear flows: Transition and control. Phys. Rev. Lett. 98 (20), 204501.Google Scholar
Wedin, H. & Kerswell, R. R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.Google Scholar
Woodcock, J. D. & Marusic, I. 2015 The statistical behaviour of attached eddies. Phys. Fluids 27 (1), 015104–25.Google Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.Google Scholar
Zammert, S. & Eckhardt, B. 2016 Harbingers and latecomers – the order of appearance of exact coherent structures in plane Poiseuille flow. J. Turbul. 18 (2), 103–114.Google Scholar