Hostname: page-component-66d9dcfd78-nqrk7 Total loading time: 0 Render date: 2026-08-08T03:34:01.331Z Has data issue: false hasContentIssue false
  • English
  • Français

Flexible scraping of viscous fluids

Published online by Cambridge University Press:  09 January 2013

Jacopo Seiwert ,
David Quéré  and
Christophe Clanet
Jacopo Seiwert
Affiliation:
LadHyX, UMR 7646 du CNRS, École Polytechnique, 91128 Palaiseau CEDEX, France Physique et Mécanique des milieux hétérogènes, UMR 7636 du CNRS, ESPCI, 75005 Paris, France
David Quéré
Affiliation:
LadHyX, UMR 7646 du CNRS, École Polytechnique, 91128 Palaiseau CEDEX, France Physique et Mécanique des milieux hétérogènes, UMR 7636 du CNRS, ESPCI, 75005 Paris, France
Christophe Clanet*
Affiliation:
LadHyX, UMR 7646 du CNRS, École Polytechnique, 91128 Palaiseau CEDEX, France Physique et Mécanique des milieux hétérogènes, UMR 7636 du CNRS, ESPCI, 75005 Paris, France
*
†Email address for correspondence: clanet@ladhyx.polytechnique.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

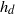We study the thickness ${h}_{d} $ of the liquid film left on a wet surface after scraping it with an elastic wiper (length 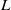$L$, rigidity 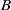$B$) moved at a velocity 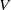$V$. The scraper is clamped vertically at a given distance above the substrate, and 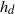${h}_{d} $ is maximal when the tip of the scraper is just tangent to the surface. We show experimentally and theoretically that this maximum thickness is 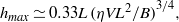${h}_{\mathit{max}} \simeq 0. 33L \mathop{ (\eta V{L}^{2} / B)}\nolimits ^{3/ 4} , $ where 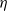$\eta $ is the liquid viscosity. The deposition law is found to be sensitive to the shape of the wiper: the film thickness can also be tuned by using wipers with a permanent curvature, and varying this curvature.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Low-Reynolds-number flows: Low-Reynolds-number flows Interfacial Flows (free surface): Thin films

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 715 , 25 January 2013 , pp. 424 - 435
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bretherton, F. P. 1961 The motion of long bubbles in tubes. J. Fluid Mech. 10, 166–188.CrossRefGoogle Scholar
Corvolan, C. M. & Saita, F. A. 1995 Blade coating on a compressible substrate. Chem. Engng Sci. 50, 1769–1783.Google Scholar
Derjaguin, B. 1943 On the thickness of the liquid film adhering to the walls of a vessel after emptying. Acta Physicochim. USSR 20, 349–352.Google Scholar
Eklund, D. E. 1984 Influence of blade geometry and blade pressure on the appearance of a coated surface. In Proceedings of the 1984 TAPPI Coating Conference, pp. 37–43.Google Scholar
Hosoi, A. E. & Mahadevan, L. 2004 Peeling, healing, and bursting in a lubricated elastic sheet. Phys. Rev. Lett. 93, 137802.Google Scholar
Iliopoulos, I. & Scriven, L. E. 2005 A blade coating study using a finite-element simulation. Phys. Fluids 17, 127101.CrossRefGoogle Scholar
Kistler, S. F. & Schweizer, P. M. 1997 Liquid Film Coating. Chapman & Hall.CrossRefGoogle Scholar
Landau, L. & Levich, B. 1942 Dragging of a liquid by a moving plate. Acta Physicochim. USSR 17, 42–54.Google Scholar
Landau, L., Lifshitz, E. & Kosevich, A. 1990 Theory of Elasticity. Mir.Google Scholar
Mahadevan, L. & Keller, J. B. 1999 Periodic folding of thin sheets. SIAM Rev. 41, 115–131.Google Scholar
Pranckh, F. R. & Scriven, L. E. 1990 Elastohydrodynamics of blade coating. AIChE J. 36, 587–597.Google Scholar
Ramdane, O. O. & Quere, D. 1997 Thickening factor in Marangoni coating. Langmuir 13, 2911–2916.CrossRefGoogle Scholar
Saita, F. A. 1989 Simplified models of flexible blade coating. Chem. Engng Sci. 44, 817–825.CrossRefGoogle Scholar
Shen, A. Q., Gleason, B., McKinley, G. H. & Stone, H. A. 2002 Fiber coating with surfactant solutions. Phys. Fluids 14, 4055–4068.Google Scholar
Sullivan, T. M. & Middleman, S. 1986 Film thickness in blade coating of viscous and viscoelastic liquids. J. Non-Newtonian Fluid Mech. 21, 13–38.CrossRefGoogle Scholar
Taylor, G. I. 1962 On scraping viscous fluid from a plane surface. In Miszellaneen der Angewandten Mechanik (Festschrift Walter Tollmien), pp. 313–315.Google Scholar