Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T02:38:07.121Z Has data issue: false hasContentIssue false
  • English
  • Français

Flow past a rotationally oscillating cylinder

Published online by Cambridge University Press:  24 October 2013

S. Kumar ,
C. Lopez ,
O. Probst ,
G. Francisco ,
D. Askari  and
Y. Yang
S. Kumar*
Affiliation:
School of Engineering and Computational Science, The University of Texas at Brownsville, Brownsville, TX 78520, USA
C. Lopez
Affiliation:
School of Engineering and Computational Science, The University of Texas at Brownsville, Brownsville, TX 78520, USA
O. Probst
Affiliation:
Physics Department, Instituto Tecnológico y de Estudios Superiores de Monterrey, Monterrey, Mexico
G. Francisco
Affiliation:
School of Engineering and Computational Science, The University of Texas at Brownsville, Brownsville, TX 78520, USA
D. Askari
Affiliation:
School of Engineering and Computational Science, The University of Texas at Brownsville, Brownsville, TX 78520, USA
Y. Yang
Affiliation:
School of Engineering and Computational Science, The University of Texas at Brownsville, Brownsville, TX 78520, USA
*
†Email address for correspondence: Sanjay.Kumar@utb.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Flow past a circular cylinder executing sinusoidal rotary oscillations about its own axis is studied experimentally. The experiments are carried out at a Reynolds number of 185, oscillation amplitudes varying from 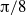$\mathrm{\pi} / 8$ to 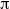$\mathrm{\pi} $, and at non-dimensional forcing frequencies (ratio of the cylinder oscillation frequency to the vortex-shedding frequency from a stationary cylinder) varying from 0 to 5. The diagnostic is performed by extensive flow visualization using the hydrogen bubble technique, hot-wire anemometry and particle-image velocimetry. The wake structures are related to the velocity spectra at various forcing parameters and downstream distances. It is found that the phenomenon of lock-on occurs in a forcing frequency range which depends not only on the amplitude of oscillation but also the downstream location from the cylinder. The experimentally measured lock-on diagram in the forcing amplitude and frequency plane at various downstream locations ranging from 2 to 23 diameters is presented. The far-field wake decouples, after the lock-on at higher forcing frequencies and behaves more like a regular Bénard–von Kármán vortex street from a stationary cylinder with vortex-shedding frequency mostly lower than that from a stationary cylinder. The dependence of circulation values of the shed vortices on the forcing frequency reveals a decay character independent of forcing amplitude beyond forcing frequency of 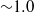${\sim }1. 0$ and a scaling behaviour with forcing amplitude at forcing frequencies 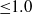${\leq }1. 0$. The flow visualizations reveal that the far-field wake becomes two-dimensional (planar) near the forcing frequencies where the circulation of the shed vortices becomes maximum and strong three-dimensional flow is generated as mode shape changes in certain forcing parameter conditions. It is also found from flow visualizations that even at higher Reynolds number of 400, forcing the cylinder at forcing amplitudes of 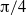$\mathrm{\pi} / 4$ and 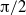$\mathrm{\pi} / 2$ can make the flow field two-dimensional at forcing frequencies greater than 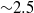${\sim }2. 5$.

JFM classification

Vortex Flows: Vortex shedding Wakes/Jets: Vortex streets Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 735 , 25 November 2013 , pp. 307 - 346
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Badr, H. M. & Dennis, S. C. R. 1985 Time-dependent viscous flow past an impulsively started rotating and translating circular cylinder. J. Fluid Mech. 158, 447–488.Google Scholar
Baek, S.-J. & Hyung, J. S. 1998 Numerical simulation of the flow behind a rotary oscillating circular cylinder. Phys. Fluids 10 (4), 869–876.Google Scholar
Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16, 195–222.Google Scholar
Berger, E. & Willie, R. 1972 Periodic flow phenomenon. Annu. Rev. Fluid Mech. 4, 313–340.Google Scholar
Bergmann, M., Cordier, L. & Brnacher, J.-P. 2006 On the generation of a reverse von Kármán street for the controlled cylinder wake in the laminar regime. Phys. Fluids 18, 028101.CrossRefGoogle Scholar
Bishop, R. E. D & Hassan, A. Y. 1964 The lift and drag forces on a circular cylinder oscillating in a flowing fluid. Proc. R. Soc. Lond. Ser. A 227, 51–75.Google Scholar
Cheng, M., Chew, T. & Luo, S. C. 2001 Numerical investigation of a rotationally oscillating cylinder in mean flow. J. Fluids Struct. 15, 981–1007.Google Scholar
Choi, S., Choi, H. & Kang, S. 2002 Characteristics of flow over a rotationally oscillating cylinder at low Reylonds number. Phys. Fluids 14 (8), 2767–2777.Google Scholar
Chyu, C., Lin, J.-C, Sheridan, J. & Rockwell, D. 1995 Kármán vortex formation from a cylinder: role of phase-locked Kelvin–Helmholtz vortices. Phys. Fluids 7 (9), 2288–2290.CrossRefGoogle Scholar
Chyu, C. K. & Rockwell, D. 1996 Near wake structure of an oscillating cylinder: effect of controlled shear layer vortices. J. Fluid Mech. 322, 21–49.Google Scholar
Cimbala, J. M., Nagib, H. M & Roshko, A. 1988 Large structure in the far wakes of two-dimensional bluff bodies. J. Fluid Mech. 190, 265–298.CrossRefGoogle Scholar
Deng, J., Shao, X.-M. & Ren, A.-L. 2007 Vanishing of three-dimensionality in the wake behind a rotationally oscillating circular cylinder. J. Hydrodyn. 19 (6), 751–755.CrossRefGoogle Scholar
Dennis, S. C. R., Nguyen, P. & Kocabiyik, S. 2000 The flow induced by a rotationally oscillating and translating circular cylinder. J. Fluid Mech. 407, 123–144.Google Scholar
Filler, J. R., Marston, P. L & Mih, W. C. 1991 Response of the shear layers separating from a circular cylinder to small-amplitude rotational oscillations. J. Fluid Mech. 231, 481–499.Google Scholar
Fujisawa, N., Kawaji, Y. & Ikemoto, K. 2001 Feedback control of vortex shedding from a circular cylinder by rotational oscillations. J. Fluids Struct. 15, 23–37.Google Scholar
Fujisawa, N., Tanahashi, S. & Srinivas, K. 2005 Evaluation of pressure field and fluid forces on a circular cylinder with and without rotational oscillation using velocity data from PIV measurement. Meas. Sci. Technol. 16, 989–996.Google Scholar
Griffin, O. M. & Ramberg, S. E. 1976 Vortex shedding from a circular cylinder vibrating in line with an incipient uniform flow. J. Fluid Mech. 75, 257–271.Google Scholar
Gu, W., Chyu, C. & Rockwell, D. 1994 Timing of vortex formation from an oscillating cylinder. Phys. Fluids 6 (11), 3677–3682.CrossRefGoogle Scholar
He, J.-W., Glowinski, R., Metcalfe, R., Nordlander, A. & Periaux, J. 2000 Active control and drag optimization for flow past a circular cylinder. I. Oscillatory cylinder rotation. J. Comput. Phys. 163, 83–117.Google Scholar
Hourigan, K., Thompson, M. C., Sheard, G. J., Ryan, K., Leontini, J. S. & Johnson, S. A. 2007 Low Reynolds number instabilities and transitions in bluff body wakes. J. Phys.: Conf. Ser. 64, 012018.Google Scholar
Hurlbut, S. E., Spaulding, M. L. & White, F. M. 1982 Numerical solution for laminar two-dimensional flow about a cylinder oscillating in a uniform stream. ASME J. Fluids Engng 104, 214–220.Google Scholar
Jacono, D. L., Leontini, J. S., Thompson, M. C. & Sheridan, J. 2010 Modifications of three-dimensional transition in the wake of a rotationally oscillating cylinder. J. Fluid Mech. 643, 349–362.Google Scholar
von Kármán, T. 1911 Über den Mechanismus des Widerstands, den ein bewegter Körper in einer Flüssigkeit erfährt. Göttinger Nachrichten, Math. Phys. Kl. 509–517.Google Scholar
von Kármán, T. 1912 Über den Mechanismus des Widerstands, den ein bewegter Körper in einer Flüssigkeit erfährt. Göttinger Nachrichten, Math. Phys. Kl. 547–556.Google Scholar
Konstantinidis, E., Balabani, S. & Yianneskis, M. 2005 Conditional averaging of PIV plane wake data using a cross-correlation approach. Exp. Fluids 39 (1), 38–47.CrossRefGoogle Scholar
Kumar, S., Cantu, C. & Gonzalez, B. 2011b Flow past a rotating cylinder at low and high rotation rates. ASME J. Fluids Engng 133, 041201.Google Scholar
Kumar, S., Gonzalez, B. & Probst, O. 2011a Flow past two rotating cylinders. Phys. Fluids 23, 014102.Google Scholar
Kumar, S., Laughlin, G. & Cantu, C. 2009 Near-wake structure behind two circular cylinders in a side-by-side configuration with heat release. Phys. Rev. E 80, 066307.Google Scholar
Lamb, H. 1932 Hydrodynamics, 6th edn, pp. 224–229. Dover.Google Scholar
Lee, S. & Lee, J. 2006 Flow structure of a wake behind a rotationally oscillating circular cylinder. J. Fluids Struct. 22, 1097–1112.Google Scholar
Lee, S.-J. & Lee, J.-Y. 2008 PIV measurements of the wake behind a rotationally oscillating circular cylinder. J. Fluids Struct. 24, 2–17.Google Scholar
Lu, M.-Y. & Sato, J. 1996 A numerical study of flow past a rotationally oscillating cylinder. J. Fluids Struct. 10, 829–849.Google Scholar
Lu, L., Qin, J.-Min, B. Teng & Li, Y.-Cheng 2011 Numerical investigations of lift suppression by feedback rotary oscillation of circular cylinder at low Reynolds number. Phys. Fluids 23, 033601.Google Scholar
Mahfouz, F. M. & Badr, H. M. 2000 Flow structure in the wake of a rotationally oscillating cylinder. ASME J. Fluids Engng 122, 290–301.Google Scholar
Nazarinia, M., Lo Jocono, D., Thomson, M. C. & Sheridan, J. 2009 The three-dimensional wake of a cylinder undergoing a combination of translational and rotational oscillation in a quiescient fluid. Phys. Fluids 21, 064101.Google Scholar
Negri, M., Cozzi, F. & Malavasi, S. 2011 Self-synchronized phase averaging of PIV measurements in the base region of a rectangular cylinder. Meccanica 46 (2), 423–435.CrossRefGoogle Scholar
Okajima, A., Takata, H. & Asanuma, T. 1975 Viscous flow around a rotationally oscillating circular cylinder. Inst. Space Aero. Sci. Rep. 532, University of Tokyo.Google Scholar
Poncet, P. 2002 Vanishing of mode B in the wake behind a rotationally oscillating circular cylinder. Phys. Fluids 14 (7), 2073–2087.CrossRefGoogle Scholar
Poncet, P. 2004 Topological aspects of three-dimensional wakes behind rotary oscillating cylinders. J. Fluid Mech. 517, 27–53.Google Scholar
Prandtl, L. 1925 Die Naturwissenschaften, 13, pp. 93–108. (English translation: Applications of the Magnus effect to the wind propulsion of ships. NACA Tech. Mem. 387, June (1926).).Google Scholar
Prasad, A. & Williamson, C. H. K. 1997 The instability of the shear layer separating from a bluff body. J. Fluid Mech. 333, 375–402.Google Scholar
Protas, B. & Wesfreid, J. E. 2002 Drag force in the open-loop control of the cylinder wake in the laminar regime. Phys. Fluids 14 (2), 810–826.Google Scholar
Shiels, D. & Leonard, A. 2001 Investigation of a drag reduction on a circular cylinder in rotary oscillation. J. Fluid Mech. 431, 297–322.Google Scholar
Taneda, S. 1978 Visual observations of the flow past a circular cylinder performing a rotary oscillation. J. Phys. Soc. Japan 45 (3), 1038–1043.Google Scholar
Tanida, Y., Okajima, A. & Watanabe, Y. 1973 Stability of the circular cylinder oscillating in a uniform flow or in a wake. J. Fluid Mech. 61, 769–784.Google Scholar
Thiria, B., Goujon-Durand, S. & Wesfreid, J. E. 2006 The wake of a cylinder performing rotary oscillations. J. Fluid Mech. 560, 123–147.Google Scholar
Thiria, B. & Wesfreid, J. E. 2007 Stability properties of forced wakes. J. Fluid Mech. 579, 137–161.Google Scholar
Tokumaru, P. T. & Dimotakis, P. E. 1991 Rotary oscillation control of a cylinder wake. J. Fluid Mech. 224, 77–90.CrossRefGoogle Scholar
Tokumaru, P. T. & Dimotakis, P. E. 1993 The lift of a cylinder executing rotary motions in a uniform flow. J. Fluid Mech. 255, 1–10.Google Scholar
Wei, T. & Smith, C. R. 1986 Secondary vortices in the wake of circular cylinders. J. Fluid Mech. 169, 513–533.Google Scholar
Weihs, D. 1972 Semi infinite vortex trails, and their relation to oscillating aerofoils. J. Fluid Mech. 54, 679–690.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Williamson, C. H. K & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2, 355–381.CrossRefGoogle Scholar

Kumar supplementary movie

Caption: Far wake structure at oscillation amplitude of pi by 2 and forcing frequency ratio of 0.8 at Re = 185.

Download Kumar supplementary movie(Video)
Video 11.6 MB

Kumar supplementary movie

Caption: Far wake structure at oscillation amplitude of pi by 2 and forcing frequency ratio of 0.25 at Re = 185.

Download Kumar supplementary movie(Video)
Video 19.3 MB

Kumar supplementary movie

Caption: Far wake structure at oscillation amplitude of pi by 2 and forcing frequency ratio of 1.0 at Re = 185.

Download Kumar supplementary movie(Video)
Video 19.3 MB

Kumar supplementary movie

Caption: Far wake structure at oscillation amplitude of pi by 2 and forcing frequency ratio of 4.5 at Re = 185.

Download Kumar supplementary movie(Video)
Video 15.5 MB

Kumar supplementary movie

Caption: Near wake structure at oscillation amplitude of pi by 2 and forcing frequency ratio of 0.8 at Re = 185.

Download Kumar supplementary movie(Video)
Video 11.6 MB

Kumar supplementary movie

Caption: Near wake structure at oscillation amplitude of pi by 2 and forcing frequency ratio of 0.25 at Re = 185.

Download Kumar supplementary movie(Video)
Video 19.3 MB

Kumar supplementary movie

Caption: Near wake structure at oscillation amplitude of pi by 2 and forcing frequency ratio of 1.0 at Re = 185.

Download Kumar supplementary movie(Video)
Video 11.6 MB

Kumar supplementary movie

Caption: Near wake structure at oscillation amplitude of pi by 2 and forcing frequency ratio of 1.2 at Re = 185.

Download Kumar supplementary movie(Video)
Video 11.6 MB

Kumar supplementary movie

Caption: Near wake structure at oscillation amplitude of pi by 2 and forcing frequency ratio of 4.5 at Re = 185.

Download Kumar supplementary movie(Video)
Video 11.6 MB