Article contents
The fluid dynamics of rolling wheels at low Reynolds number
Published online by Cambridge University Press: 20 July 2012
Abstract
We study the fluid dynamics of rolling wheels at Reynolds number 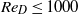 (where
(where 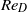 is the Reynolds number based on the wheel diameter), with the objective of characterizing the various regimes of steady and unsteady motion. Regardless of the Reynolds number, the flow is found to separate approximately
is the Reynolds number based on the wheel diameter), with the objective of characterizing the various regimes of steady and unsteady motion. Regardless of the Reynolds number, the flow is found to separate approximately 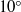 upstream of the apex of the wheel, where a saddle point in the pseudo-streamtrace pattern is observed. Under the flow conditions here essayed, the drag coefficient steadily decreases with
upstream of the apex of the wheel, where a saddle point in the pseudo-streamtrace pattern is observed. Under the flow conditions here essayed, the drag coefficient steadily decreases with  , and the lift coefficient remains strictly positive. The positive lift provided by the rolling wheel is associated with the presence of a strong (positive) peak of the static pressure in the upstream proximity of the contact point with the ground, which we interpret as the result of the impingement of flow particles entrained in the boundary layer that develops on the front part of the wheel. Steady laminar flow is observed up to
, and the lift coefficient remains strictly positive. The positive lift provided by the rolling wheel is associated with the presence of a strong (positive) peak of the static pressure in the upstream proximity of the contact point with the ground, which we interpret as the result of the impingement of flow particles entrained in the boundary layer that develops on the front part of the wheel. Steady laminar flow is observed up to  , which is characterized by a three-dimensional wake whose length increases with the Reynolds number. Unsteadiness is first observed at
, which is characterized by a three-dimensional wake whose length increases with the Reynolds number. Unsteadiness is first observed at 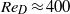 , under which conditions the flow retains planar symmetry, and is characterized by the quasi-periodic shedding of hairpin vortices. Transition to three-dimensional flow happens at
, under which conditions the flow retains planar symmetry, and is characterized by the quasi-periodic shedding of hairpin vortices. Transition to three-dimensional flow happens at 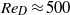 , in which case a sinuous mode of instability in the wheel wake is established, which modulates the shedding of the hairpins, and which causes the onset of a non-zero side force. At the highest Reynolds number considered here (
, in which case a sinuous mode of instability in the wheel wake is established, which modulates the shedding of the hairpins, and which causes the onset of a non-zero side force. At the highest Reynolds number considered here (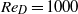 ) the wake exhibits some characters of turbulence, with wide-band frequency spectra, and its topology entirely changes, becoming split into two parts, and being much shortened compared to the lower-
) the wake exhibits some characters of turbulence, with wide-band frequency spectra, and its topology entirely changes, becoming split into two parts, and being much shortened compared to the lower-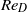 cases. Despite the limitation of the study to low Reynolds numbers we find that, once significant three-dimensionality and scale separation are established in the wheel wake, the nature of the flow becomes qualitatively similar to fully developed turbulent flow. In perspective, this observation opens interesting avenues for the prediction of unsteady flow around rotating tyres at moderate computational cost.
cases. Despite the limitation of the study to low Reynolds numbers we find that, once significant three-dimensionality and scale separation are established in the wheel wake, the nature of the flow becomes qualitatively similar to fully developed turbulent flow. In perspective, this observation opens interesting avenues for the prediction of unsteady flow around rotating tyres at moderate computational cost.
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 19
- Cited by

