We study theoretically and numerically the downstream flow near the corner of a bluff body partially submerged at a deadrise depth ${\rm\Delta}h$ into a uniform stream of velocity 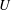$U$, in the presence of gravity, 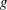$g$. When the Froude number, 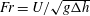$\mathit{Fr}=U/\sqrt{g{\rm\Delta}h}$, is large, a three-dimensional steady plunging wave, which is referred to as a corner wave, forms near the corner, developing downstream in a similar way to a two-dimensional plunging wave evolving in time. We have performed an asymptotic analysis of the flow near this corner to describe the wave’s initial evolution and to clarify the physical mechanism that leads to its formation. Using the two-dimensions-plus-time approximation, the problem reduces to one similar to dam-break flow with a wet bed in front of the dam. The analysis shows that, at leading order, the problem admits a self-similar formulation when the size of the wave is small compared with the height difference 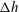${\rm\Delta}h$. The essential feature of the self-similar solution is the formation of a mushroom-shaped jet from which two smaller lateral jets stem. However, numerical simulations show that this self-similar solution is questionable from the physical point of view, as the two lateral jets plunge onto the free surface, leading to a self-intersecting flow. The physical mechanism leading to the formation of the mushroom-shaped structure is discussed.