Published online by Cambridge University Press: 25 September 2023
We study the effect of a confined turbulent counter-current gas flow on the waviness of a weakly inclined falling liquid film. Our study is centred on experiments in a channel of 13 mm height, using water and air, where we have successively increased the counter-current gas flow rate until flooding. Computations with a new low-dimensional model and linear stability calculations are used to elucidate the linear and nonlinear wave dynamics. We find that the gas pressure gradient plays an important role in countering the stabilizing effect of the tangential gas shear stress at the liquid–gas interface. At very low inclination angles, the latter effect dominates and can suppress the long-wave Kapitza instability unconditionally. By contrast, for non-negligible inclination, the gas effect is linearly destabilizing, amplifies the height of nonlinear Kapitza waves, and exacerbates coalescence-induced formation of large-amplitude tsunami waves. Kapitza waves do not undergo any catastrophic transformation when the counter-current gas flow rate is increased beyond the absolute instability (AI) limit. On the contrary, we find that AI is an effective linear wave selection mechanism in a noise-driven wave evolution scenario, leading to highly regular downward-travelling nonlinear wave trains, which preclude coalescence events. In our experiments, where Kapitza waves develop in a protected region before coming into contact with the gas, flooding is eventually caused far beyond the AI limit by upward-travelling short-wave ripples. Based on our linear stability calculations for arbitrary wavenumbers, we have uncovered a new short-wave interfacial instability mode with negative linear wave speed, causing these ripples.
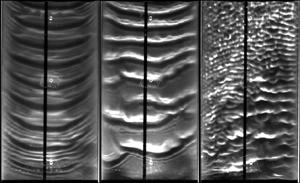
Gas-induced wave coalescence on a weakly-inclined falling liquid film subject to a counter-current turbulent gas flow. Parameters according to panel 18b: below the absolute instability limit.