Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-22T04:47:42.592Z Has data issue: false hasContentIssue false
  • English
  • Français

Hairpin vortices and highly elongated flow structures in a stably stratified shear layer

Published online by Cambridge University Press:  04 September 2019

Tomoaki Watanabe Open the ORCID record for Tomoaki Watanabe [Opens in a new window] ,
James J. Riley ,
Koji Nagata Open the ORCID record for Koji Nagata [Opens in a new window] ,
Keigo Matsuda  and
Ryo Onishi
Tomoaki Watanabe*
Affiliation:
Department of Aerospace Engineering, Nagoya University, Nagoya 464-8603, Japan
James J. Riley
Affiliation:
Department of Mechanical Engineering, University of Washington, Seattle 98195, USA
Koji Nagata
Affiliation:
Department of Aerospace Engineering, Nagoya University, Nagoya 464-8603, Japan
Keigo Matsuda
Affiliation:
Center for Earth Information Science and Technology (CEIST), Japan Agency for Marine-Earth Science and Technology, Yokohama 236-0001, Japan
Ryo Onishi
Affiliation:
Center for Earth Information Science and Technology (CEIST), Japan Agency for Marine-Earth Science and Technology, Yokohama 236-0001, Japan
*
†Email address for correspondence: watanabe.tomoaki@c.nagoya-u.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

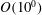Turbulent structures in stably stratified shear layers are studied with direct numerical simulation. Flow visualization confirms the existence of hairpin vortices and highly elongated structures with positive and negative velocity fluctuations, whose streamwise lengths divided by the layer thickness are $O(10^{0})$ and 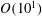$O(10^{1})$, respectively. The flow at the wavelength related to these structures makes a large contribution to turbulent kinetic energy. These structures become prominent in late time, but with small buoyancy Reynolds numbers indicating suppression of turbulent mixing. Active turbulent mixing associated with the hairpin vortices, however, does occur. The structures and the vertical profile of the integral shear parameter show connections between stable stratified shear layers and wall-bounded shear flows.

JFM classification

Turbulent Flows: Stratified turbulence Wakes/Jets: Shear layers Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 878 , 10 November 2019 , pp. 37 - 61
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Antonia, R. A. & Zhao, Q. 2001 Effect of initial conditions on a circular jet. Exp. Fluids 31 (3), 319–323.Google Scholar
Barry, M. E., Ivey, G. N., Winters, K. B. & Imberger, J. 2001 Measurements of diapycnal diffusivities in stratified fluids. J. Fluid Mech. 442, 267–291.Google Scholar
Brucker, K. A. & Sarkar, S. 2007 Evolution of an initially turbulent stratified shear layer. Phys. Fluids 19 (10), 105105.Google Scholar
Carlier, J. & Stanislas, M. 2005 Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry. J. Fluid Mech. 535, 143–188.Google Scholar
Corrsin, S. & Kistler, A. L.1955 Free-stream boundaries of turbulent flows. NACA Tech. Rep. TN-1244.Google Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
De Silva, I. P. D., Fernando, H. J. S., Eaton, F. & Hebert, D. 1996 Evolution of Kelvin–Helmholtz billows in nature and laboratory. Earth Planet. Sci. Lett. 143 (1), 217–231.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011 Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 673, 180–217.Google Scholar
Fernando, H. J. S. 1991 Turbulent mixing in stratified fluids. Annu. Rev. Fluid Mech. 23 (1), 455–493.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.Google Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.Google Scholar
Hellström, L. H. O., Sinha, A. & Smits, A. J. 2011 Visualizing the very-large-scale motions in turbulent pipe flow. Phys. Fluids 23 (1), 011703.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Jiménez, J. 2013 How linear is wall-bounded turbulence? Phys. Fluids 25 (11), 110814.Google Scholar
Jiménez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, P1.Google Scholar
Katzwinkel, J., Siebert, H. & Shaw, R. A. 2012 Observation of a self-limiting, shear-induced turbulent inversion layer above marine stratocumulus. Boundary-Layer Meteorol. 145 (1), 131–143.Google Scholar
Kempf, A., Klein, M. & Janicka, J. 2005 Efficient generation of initial-and inflow-conditions for transient turbulent flows in arbitrary geometries. Flow Turbul. Combust. 74 (1), 67–84.Google Scholar
Kida, S. & Miura, H. 1998 Identification and analysis of vortical structures. Eur. J. Mech. B 17 (4), 471–488.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Krug, D., Holzner, M., Lüthi, B., Wolf, M., Kinzelbach, W. & Tsinober, A. 2015 The turbulent/non-turbulent interface in an inclined dense gravity current. J. Fluid Mech. 765, 303–324.Google Scholar
de Lavergne, C., Madec, G., Le Sommer, J., Nurser, A. J. G. & Naveira Garabato, A. C. 2016 The impact of a variable mixing efficiency on the abyssal overturning. J. Phys. Oceanogr. 46 (2), 663–681.Google Scholar
Lee, J. H. & Sung, H. J. 2013 Comparison of very-large-scale motions of turbulent pipe and boundary layer simulations. Phys. Fluids 25 (4), 045103.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Malinowski, S. P., Gerber, H., Plante, J.-L., Kopec, M. K., Kumala, W., Nurowska, K., Chuang, P. Y., Khelif, D., Haman, K. E. et al. 2013 Physics of Stratocumulus Top (POST): turbulent mixing across capping inversion. Atmos. Chem. Phys 13 (24), 12171–12186.Google Scholar
Mashayek, A., Caulfield, C. P. & Peltier, W. R. 2017 Role of overturns in optimal mixing in stratified mixing layers. J. Fluid Mech. 826, 522–552.Google Scholar
Mashayek, A. & Peltier, W. R. 2012a The ‘zoo’ of secondary instabilities precursory to stratified shear flow transition. Part 1 Shear aligned convection, pairing, and braid instabilities. J. Fluid Mech. 708, 5–44.Google Scholar
Mashayek, A. & Peltier, W. R. 2012b The ‘zoo’ of secondary instabilities precursory to stratified shear flow transition. Part 2 The influence of stratification. J. Fluid Mech. 708, 45–70.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mellado, J. P. 2017 Cloud-top entrainment in stratocumulus clouds. Annu. Rev. Fluid Mech. 49, 145–169.Google Scholar
Mellado, J. P., Stevens, B. & Schmidt, H. 2014 Wind shear and buoyancy reversal at the top of stratocumulus. J. Atmos. Sci. 71 (3), 1040–1057.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.Google Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.Google Scholar
Moum, J. N. 1996 Efficiency of mixing in the main thermocline. J. Geophys. Res. 101 (C5), 12057–12069.Google Scholar
Ooi, A., Martin, J., Soria, J. & Chong, M. S. 1999 A study of the evolution and characteristics of the invariants of the velocity-gradient tensor in isotropic turbulence. J. Fluid Mech. 381, 141–174.Google Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35 (1), 135–167.Google Scholar
Pham, H. T., Sarkar, S. & Winters, K. B. 2012 Intermittent patches of turbulence in a stratified medium with stable shear. J. Turbul. (13), N20.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Riley, J. J. & Lindborg, E. 2008 Stratified turbulence: a possible interpretation of some geophysical turbulence measurements. J. Atmos. Sci. 65 (7), 2416–2424.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.Google Scholar
Rogers, M. M. & Moser, R. D. 1994 Direct simulation of a self-similar turbulent mixing layer. Phys. Fluids 6 (2), 903–923.Google Scholar
Salehipour, H., Peltier, WR. & Mashayek, A. 2015 Turbulent diapycnal mixing in stratified shear flows: the influence of Prandtl number on mixing efficiency and transition at high Reynolds number. J. Fluid Mech. 773, 178–223.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Sekimoto, A., Dong, S. & Jiménez, J. 2016 Direct numerical simulation of statistically stationary and homogeneous shear turbulence and its relation to other shear flows. Phys. Fluids 28 (3), 035101.Google Scholar
Shih, L. H., Koseff, J. R., Ivey, G. N. & Ferziger, J. H. 2005 Parameterization of turbulent fluxes and scales using homogeneous sheared stably stratified turbulence simulations. J. Fluid Mech. 525, 193–214.Google Scholar
da Silva, C. B., Dos Reis, R. J. N. & Pereira, J. C. F. 2011 The intense vorticity structures near the turbulent/non-turbulent interface in a jet. J. Fluid Mech. 685, 165–190.Google Scholar
da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46, 567–590.Google Scholar
da Silva, C. B. & Pereira, J. C. F. 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets. Phys. Fluids 20 (5), 055101.Google Scholar
Smyth, W. D. 2006 Secondary circulations in Holmboe waves. Phys. Fluids 18 (6), 064104.Google Scholar
Smyth, W. D. & Moum, J. N. 2000a Anisotropy of turbulence in stably stratified mixing layers. Phys. Fluids 12 (6), 1343–1362.Google Scholar
Smyth, W. D. & Moum, J. N. 2000b Length scales of turbulence in stably stratified mixing layers. Phys. Fluids 12 (6), 1327–1342.Google Scholar
Smyth, W. D. & Winters, K. B. 2003 Turbulence and mixing in Holmboe waves. J. Phys. Oceanogr. 33 (4), 694–711.Google Scholar
Strang, E. J. & Fernando, H. J. S. 2001 Entrainment and mixing in stratified shear flows. J. Fluid Mech. 428, 349–386.Google Scholar
Thorpe, S. A. 1973a Experiments on instability and turbulence in a stratified shear flow. J. Fluid Mech. 61 (4), 731–751.Google Scholar
Thorpe, S. A. 1973b Turbulence in stably stratified fluids: a review of laboratory experiments. Boundary-Layer Meteorol. 5 (1–2), 95–119.Google Scholar
Venayagamoorthy, S. K. & Stretch, D. D. 2006 Lagrangian mixing in decaying stably stratified turbulence. J. Fluid Mech. 564, 197–226.Google Scholar
Watanabe, T., Riley, J. J. & Nagata, K. 2016 Effects of stable stratification on turbulent/nonturbulent interfaces in turbulent mixing layers. Phys. Rev. Fluids 1 (4), 044301.Google Scholar
Watanabe, T., Riley, J. J. & Nagata, K. 2017 Turbulent entrainment across turbulent-nonturbulent interfaces in stably stratified mixing layers. Phys. Rev. Fluids 2 (10), 104803.Google Scholar
Watanabe, T., Riley, J. J., Nagata, K., Onishi, R. & Matsuda, K. 2018 A localized turbulent mixing layer in a uniformly stratified environment. J. Fluid Mech. 849, 245–276.Google Scholar
Williams, O. J. H.2014 Density effects on turbulent boundary layer structure: from the atmosphere to hypersonic flow. PhD thesis, Princeton University, Princeton, NJ.Google Scholar
Woods, J. D. 1968 Wave-induced shear instability in the summer thermocline. J. Fluid Mech. 32 (4), 791–800.Google Scholar
Wu, X., Baltzer, J. R. & Adrian, R. J. 2012 Direct numerical simulation of a 30r long turbulent pipe flow at r + = 685: large-and very large-scale motions. J. Fluid Mech. 235–281.Google Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar