Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T13:02:20.992Z Has data issue: false hasContentIssue false
  • English
  • Français

Heat transfer in a turbulent channel flow with super-hydrophobic or liquid-infused walls

Published online by Cambridge University Press:  10 December 2020

Umberto Ciri  and
Stefano Leonardi Open the ORCID record for Stefano Leonardi [Opens in a new window]
Umberto Ciri
Affiliation:
Department of Mechanical Engineering, The University of Texas at Dallas, Richardson, TX75080, USA
Stefano Leonardi*
Affiliation:
Department of Mechanical Engineering, The University of Texas at Dallas, Richardson, TX75080, USA
*
†Email address for correspondence: stefano.leonardi@utdallas.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

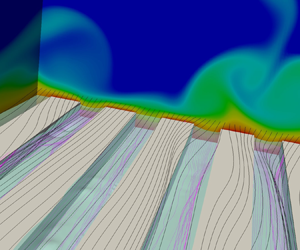
Heat transport over super-hydrophobic (SHS) and liquid-infused surfaces (LIS) is studied using direct numerical simulations of a turbulent channel flow. The lower wall of the channel consists of either longitudinal or transversal bars with a secondary fluid locked in the cavities between the surface elements. We consider two viscosity ratios between the fluids mimicking SHS and LIS. The thermal diffusivity is varied to assess its effect on thermal performance. We investigate the dependence of heat transfer on the elements pitch-to-height ratio and on the interface dynamics. The interface deformation (dependent upon the surface tension between the two fluids) is fully coupled to the fluid governing equations with the level-set method. Present simulations are consistent with published results about the drag-reducing potential of SHS and LIS in turbulent flow compared to the smooth wall. In the limiting case of infinite surface tension (the interface remains flat and slippery), heat transfer efficiency (heat transfer to drag ratio) can be enhanced compared to a smooth wall. Although the total heat flux is marginally reduced, SHS and LIS with longitudinal ridges achieve a comparatively larger drag reduction, which increases the efficiency. A model is derived from the energy equation to correlate the heat transfer performance with the thermal slip length ($b_\theta$), analogous to the streamwise slip length ($b$) used in the literature to scale drag reduction. Consistently with the model, results show that heat transfer efficiency is larger than for a smooth wall when the thermal slip length is smaller than the streamwise slip length (longitudinal bars). Vice versa, transversal bars present $b/b_\theta <1$ and a smaller heat transfer efficiency than the smooth wall. In the case of finite surface tension, the dynamics of the interface generates a turbulent flux which improves the thermal performance, but tends to decrease the amount of drag reduction. Liquid-infused surfaces are more robust than SHS to the deformation of the interface thanks to the larger viscosity of the secondary fluid and maintain about the same drag reduction as in the infinite surface tension case. For SHS longitudinal bars, simultaneous increase in heat transfer and reduction in drag are observed, leading to an apparent breakdown of the Reynolds analogy. Also in the case of finite surface tension, heat transfer efficiency scales with the relative magnitude of the thermal and streamwise slip lengths. The results suggest a potential expansion of the control space for engineers. Depending on the application, one can reach an optimal combination of heat transfer and drag by tuning the shape of the substrate and the viscosity and diffusivity ratios.

JFM classification

Turbulent Flows: Turbulence simulation Flow Control: Drag reduction Flow Control: Mixing enhancement
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 908 , 10 February 2021 , A28
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Arenas, I., García, E., Orlandi, P., Fu, M. K., Hultmark, M. & Leonardi, S. 2019 Comparison between super-hydrophobic, liquid infused and rough surfaces: a direct numerical simulation study. J. Fluid Mech. 869, 500–525.Google Scholar
Bechert, D. W., Hoppe, G. & Reif, W.-E. 1985 On the drag reduction of the shark skin. AIAA Paper 85-0546.Google Scholar
Brackbill, J. U., Kothe, D. B. & Zemach, C. 1992 A continuum method for modeling surface tension. J. Comput. Phys. 100, 335–354.Google Scholar
Chang, J., Jung, T., Choi, H. & Kim, J. 2019 Predictions of the effective slip length and drag reduction with a lubricated micro-groove surface in a turbulent channel flow. J. Fluid Mech. 874, 797–820.CrossRefGoogle Scholar
Chang, Y. C., Hou, T. Y., Merriman, B. & Osher, S. 1996 A level set formulation of Eulerian interface capturing methods for incompressible fluid flows. J. Comput. Phys. 124, 449–464.Google Scholar
Cheng, Y., Xu, J. & Sui, Y. 2015 Numerical study on drag reduction and heat transfer enhancement in microchannels with superhydrophobic surfaces for electronic cooling. Appl. Therm. Engng 88, 71–81.Google Scholar
Choi, H., Moin, P. & Kim, J. 1993 Direct numerical simulation of turbulent flow over riblets. J. Fluid Mech. 255, 503–539.CrossRefGoogle Scholar
Choi, K.-C. & Orchard, D. M. 1997 Turbulence management using riblets for heat and momentum transfer. Exp. Therm. Fluid Sci. 15, 109–124.CrossRefGoogle Scholar
Colburn, A. P. 1964 A method of correlating forced convection heat-transfer data and a comparison with fluid friction. Intl J. Heat Mass Transfer 7, 1359–1384 (reprinted from Trans. Amer. Inst. Chem. Engrs., 29, pp. 174–209, 1933).Google Scholar
Daniello, R. J., Waterhouse, N. E. & Rothstein, J. P. 2009 Drag reduction in turbulent flows over superhydrophobic surfaces. Phys. Fluids 21 (8), 085103.Google Scholar
Enright, R., Hodes, M., Salamon, T. & Muzychka, Y. 2014 Isoflux Nusselt number and slip length formulae for superhydrophobic microchannels. Trans. ASME: J. Heat Transfer 136, 012402.Google Scholar
Ekkad, S. V. & Han, J. C. 1997 Detailed heat transfer distributions in two-pass square channels with rib turbulators. Intl J. Heat Mass Transfer 40 (11), 2525–2537.Google Scholar
Ekkad, S. V., Huang, Y. & Han, J.-C. 1998 Detailed heat transfer distributions in two-pass square channels with rib turbulators and bleed holes. Intl J. Heat Mass Transfer 41 (23), 3781–3791.Google Scholar
Fu, M. K., Arenas, I., Leonardi, S. & Hultmark, M. 2017 Liquid-infused surfaces as a passive method of turbulent drag reduction. J. Fluid Mech. 824, 688–700.CrossRefGoogle Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 14 (11), L73–L76.CrossRefGoogle Scholar
Fukagata, K., Kasagi, N. & Koumoutsakos, P. 2006 A theoretical prediction of friction drag reduction in turbulent flow by superhydrophobic surfaces. Phys. Fluids 18 (5), 051703.CrossRefGoogle Scholar
García Cartagena, E. J., Arenas, I., Bernardini, M. & Leonardi, S. 2018 Dependence of the drag over super hydrophobic and liquid infused surfaces on the textured surface and Weber number. Flow Turbul. Combust. 100 (4), 945–960.CrossRefGoogle Scholar
García Cartagena, E. J., Arenas, I., An, J. & Leonardi, S. 2019 Dependence of the drag over superhydrophobic and liquid infused surfaces on the asperities of the substrate. Phys. Rev. Fluids 4, 114604.CrossRefGoogle Scholar
Gavrilakis, S. 1992 Numerical simulation of low-Reynolds-number turbulent flow through a straight square duct. J. Fluid Mech. 244, 101–129.CrossRefGoogle Scholar
Han, J. C., Dutta, S. & Ekkad, S. 2000 Gas Turbine Heat Transfer and Cooling Technology. Taylor and Francis.Google Scholar
Han, J. C. & Zhang, Y. M. 1992 High performance heat transfer ducts with parallel broken and V-shaped broken ribs. Intl J. Heat Mass Transfer 35 (2), 513–523.CrossRefGoogle Scholar
Han, J. C., Zhang, Y. M. & Lee, C. P. 1991 Augmented heat transfer in square channels with parallel, crossed, and V-shaped angled ribs. Trans. ASME: J. Heat Transfer 113, 590–596.CrossRefGoogle Scholar
Hasegawa, Y. & Kasagi, N. 2011 Dissimilar control of momentum and heat transfer in a fully developed turbulent channel flow. J. Fluid Mech. 683, 57–93.CrossRefGoogle Scholar
Hetsroni, G., Mosyak, A., Rozenblit, R. & Yarin, L. P. 1999 Thermal patterns on the smooth and rough walls in turbulent flows. Intl J. Heat Mass Transfer 42, 3815–3829.CrossRefGoogle Scholar
Hussain, A. K. M. F. & Reynolds, W. C. 1970 The mechanics of an organized wave in turbulent shear flow. J. Fluid Mech. 41, 241–258.CrossRefGoogle Scholar
Jung, T., Choi, H. & Kim, J. 2016 Effects of the air layer of an idealized superhydrophobic surface on the slip length and skin-friction drag. J. Fluid Mech. 790, R1.CrossRefGoogle Scholar
Kasagi, N., Hasegawa, Y., Fukagata, K. & Iwamoto, K. 2012 Control of turbulent transport: less friction and more heat transfer. Trans. ASME: J. Heat Transfer 134 (3), 031009.CrossRefGoogle Scholar
Kestin, J. & Richardson, P. D. 1963 Heat transfer across turbulent, incompressible boundary layers. Intl J. Heat Mass Transfer 6, 147–189.CrossRefGoogle Scholar
Kim, J. & Moin, P. 1987 Transport of passive scalars in a turbulent channel flow. In Turbulent Shear Flows (ed. J.-C. André et al. ), vol. 6, pp. 85–96. Springer.CrossRefGoogle Scholar
Kirk, T. L., Hodes, M. & Papageorgiou, D. T. 2017 Nusselt numbers for Poiseuille flow over isoflux parallel ridges accounting for meniscus curvature. J. Fluid Mech. 811, 315–349.CrossRefGoogle Scholar
Komminaho, J., Lundbladh, A. & Johansson, A. V. 1996 Very large structures in plane turbulent Couette flow. J. Fluid Mech. 320, 259–285.CrossRefGoogle Scholar
Lam, L. S., Hodes, M. & Enright, R. 2015 Analysis of Galinstan-based microgap cooling enhancement using structured surfaces. Trans. ASME: J. Heat Transfer 137, 091003.CrossRefGoogle Scholar
Lauga, E., Brenner, M. P. & Stone, H. A. 2007 Microfluidics: the no-slip boundary condition. In Handbook of Experimental Fluid Mechanics (ed. C. Tropea, A. Yarin & J. F. Foss), pp. 1219–1240. Springer.CrossRefGoogle Scholar
Leonardi, S. & Castro, I. P. 2010 Channel flow over large cube roughness: a direct numerical simulation study. J. Fluid Mech. 651, 519–539.CrossRefGoogle Scholar
Leonardi, S., Orlandi, P., Djenidi, L. & Antonia, R. A. 2004 Structure of turbulent channel flow with square bars on one wall. Intl J. Heat Fluid Flow 25, 384–392.CrossRefGoogle Scholar
Leonardi, S., Orlandi, P., Djenidi, L. & Antonia, R. A. 2015 Heat transfer in a turbulent channel flow with square bars or circular rods on one wall. J. Fluid Mech. 776, 512–530.CrossRefGoogle Scholar
Leonardi, S., Orlandi, P., Smalley, R. J, Djenidi, L. & Antonia, R. A. 2003 Direct numerical simulations of turbulent channel flow with transverse square bars on one wall. J. Fluid Mech. 491, 229–238.CrossRefGoogle Scholar
Lindemann, A. M. 1985 Turbulent Reynolds analogy factors for nonplanar surface microgeometries. J. Spacecraft 22 (5), 581–582.CrossRefGoogle Scholar
Luchini, P., Manzo, F. & Pozzi, A. 1991 Resistance of a grooved surface to parallel flow and cross-flow. J. Fluid Mech. 228, 87–109.Google Scholar
Lundbladh, A. & Johansson, A. V. 1991 Direct simulation of turbulent spots in plane Couette flow. J. Fluid Mech. 229, 499–516.CrossRefGoogle Scholar
Martell, M. B., Perot, J. B. & Rothstein, J. P. 2009 Direct numerical simulations of turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 620, 31–41.CrossRefGoogle Scholar
Maynes, D. & Crockett, J. 2014 Apparent temperature jump and thermal transport in channels with streamwise rib and cavity featured superhydrophobic walls at constant heat flux. Trans. ASME: J. Heat Transfer 136, 011701.CrossRefGoogle Scholar
Maynes, D., Webb, B. W. & Davies, J. 2008 Thermal transport in a microchannel exhibiting ultrahydrophobic micro-ribs maintained at constant temperature. Trans. ASME: J. Heat Transfer 130, 022402.CrossRefGoogle Scholar
Maynes, D., Webb, B. W., Crockett, J. & Solovjov, V. 2013 Analysis of laminar slip-flow thermal transport in microchannels with transverse rib and cavity structured superhydrophobic walls at constant heat flux. Trans. ASME: J. Heat Transfer 135, 021701.CrossRefGoogle Scholar
Miyake, Y., Tsujimoto, K. & Nakaji, M. 2001 Direct numerical simulation of a rough-wall heat transfer in a turbulent channel flow. Intl J. Heat Fluid Flow 22, 237–244.CrossRefGoogle Scholar
Ng, C.-O. & Wang, C. Y. 2014 Temperature jump coefficient for superhydrophobic surfaces. Trans. ASME: J. Heat Transfer 136, 064501.CrossRefGoogle Scholar
Orlandi, P. 2000 Fluid Flow Phenomena. A Numerical Toolkit. Kluwer Academic.CrossRefGoogle Scholar
Orlandi, P., Leonardi, S., Tuzi, R. & Antonia, R. A. 2003 Direct numerical simulation of turbulent channel flow with wall velocity disturbances. Phys. Fluids 15 (12), 3587–3601.CrossRefGoogle Scholar
Orlandi, P. & Leonardi, S. 2004 Passive scalar in a turbulent channel flow with wall velocity disturbances. Flow Turbul. Combust. 72, 181–197.CrossRefGoogle Scholar
Orlandi, P. & Leonardi, S. 2006 DNS of turbulent channel flows with two- and three-dimensional roughness. J. Turbul. 7, N53.CrossRefGoogle Scholar
Orlandi, P., Leonardi, S. & Antonia, R. A. 2008 Turbulent channel flow with either transverse or longitudinal roughness elements on one wall. J. Fluid Mech. 561, 279–305.CrossRefGoogle Scholar
Orlandi, P. & Pirozzoli, S. 2020 a Turbulent flows in square ducts: physical insight and suggestion for turbulence modellers. J. Turbul. 21 (2), 106–128.CrossRefGoogle Scholar
Orlandi, P. & Pirozzoli, S. 2020 b Transitional and turbulent flows in rectangular ducts: budgets and projection in principal mean strain axes. J. Turbul. 21 (5–6), 286–310.CrossRefGoogle Scholar
Orlandi, P., Sassun, D. & Leonardi, S. 2016 DNS of conjugate heat transfer in presence of rough surfaces. Intl J. Heat Mass Transfer 100, 250–266.CrossRefGoogle Scholar
Park, H., Park, H. & Kim, J. 2013 A numerical study of the effects of superhydrophobic surface on skin-friction drag in turbulent channel flow. Phys. Fluids 25, 110815.CrossRefGoogle Scholar
Pirozzoli, S., Modesti, D., Orlandi, P. & Grasso, F. 2018 Turbulence and secondary motions in square ducts. J. Fluid Mech. 840, 631–655.CrossRefGoogle Scholar
Promvonge, P. & Thianpong, C. 2008 Thermal performance assessment of turbulent channel flows over different shaped ribs. Intl Commun. Heat Mass 35, 1327–1334.CrossRefGoogle Scholar
Rastegari, A. & Akhavan, R. 2015 On the mechanism of turbulent drag reduction with super-hydrophobic surfaces. J. Fluid Mech. 773, R4.CrossRefGoogle Scholar
Rastegari, A. & Akhavan, R. 2018 The common mechanism of turbulent skin-friction drag reduction with superhydrophobic longitudinal microgrooves and riblets. J. Fluid Mech. 838, 68–104.CrossRefGoogle Scholar
Reynolds, O. 1961 On the extent and action of the heating surface of steam boilers. Intl J. Heat Mass Transfer 3, 163–166 (reprinted from Proc. Lit. Phil. Soc. Manchester, 14 (5), pp. 7–12, 1874).CrossRefGoogle Scholar
Rosenberg, B. J., Van Buren, T., Fu, M. K. & Smits, A. J. 2016 Turbulent drag reduction over air-and liquid-impregnated surfaces. Phys. Fluids 28 (1), 015103.CrossRefGoogle Scholar
Rosengarten, G., Stanley, C. & Kwok, F. 2007 Superinsulating heat transfer surfaces for microfluidic channels. In Proceedings of the 18th International Symposium on Transport Phenomena, Daejeon, Korea.Google Scholar
Seo, J. & Mani, A. 2016 On the scaling of the slip velocity in turbulent flows over superhydrophobic surfaces. Phys. Fluids 28 (2), 025110.CrossRefGoogle Scholar
Sethian, J. A. & Smereka, P. 2003 Level set methods for fluid interfaces. Annu. Rev. Fluid Mech. 35 (1), 341–372.CrossRefGoogle Scholar
Sewall, E. A., Tafti, K. D., Graham, A. B. & Thole, K. A. 2006 Experimental validation of large eddy simulations of flow and heat transfer in a stationary ribbed duct. Intl J. Heat Fluid Flow 27, 243–258.CrossRefGoogle Scholar
Stalio, E. & Nobile, E. 2003 Direct numerical simulation of heat transfer over riblets. Intl J. Heat Fluid Flow 24, 356–371.CrossRefGoogle Scholar
Tanda, G. 2004 Heat transfer in rectangular channels with transverse and V-shaped broken ribs. Intl J. Heat Mass Transfer 47, 229–243.CrossRefGoogle Scholar
Tachie, M. F., Paul, S. S., Agelinchaa, M. & Shah, M. K. 2009 Structure of turbulent flow over $90^\circ$ and $45^\circ$ transverse ribs. J. Turbul. 10, N20.CrossRefGoogle Scholar
Teitel, M. & Antonia, R. A. 1993 Heat transfer in fully developed turbulent channel flow: comparison between experiment and direct numerical simulations. Intl J. Heat Mass Transfer 36 (6), 1701–1706.CrossRefGoogle Scholar
Tillmark, N. & Alfredsson, P. H. 1992 Experiments on transition in plane Couette flow. J. Fluid Mech. 235, 89–102.CrossRefGoogle Scholar
Van Buren, T. & Smits, A. J. 2017 Substantial drag reduction in turbulent flow using liquid-infused surfaces. J. Fluid Mech. 827, 448–456.CrossRefGoogle Scholar
Vinuesa, R., Noorani, A., Lozano-Durán, A., El Khoury, G. K., Schlatter, P., Fischer, P. F. & Nagib, H. M. 2014 Aspect ratio effects in turbulent duct flows studied through direct numerical simulations. J. Turbul. 15 (10), 677–706.CrossRefGoogle Scholar
Walsh, M. J. 1982 Turbulent boundary layer drag reduction using riblets. AIAA Paper 82-0169.CrossRefGoogle Scholar
Walsh, M. J. 1983 Riblets as a viscous drag reduction technique. AIAA J. 21 (4), 485–486.CrossRefGoogle Scholar
Webb, R. L. 1981 Performance evaluation criteria for use of enhanced heat transfer surfaces in heat exchangers design. Intl J. Heat Mass Transfer 24 (4), 715–726.CrossRefGoogle Scholar
Won, S. Y. & Ligrani, P. M. 2004 Comparisons of flow structure and local Nusselt numbers in channels with parallel- and crossed-rib turbulators. Intl J. Heat Mass Transfer 47, 1573–1586.CrossRefGoogle Scholar