Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-10T10:57:40.891Z Has data issue: false hasContentIssue false
  • English
  • Français

Inclined porous medium convection at large Rayleigh number

Published online by Cambridge University Press:  05 January 2018

Baole Wen Open the ORCID record for Baole Wen [Opens in a new window]  and
Gregory P. Chini Open the ORCID record for Gregory P. Chini [Opens in a new window]
Baole Wen
Affiliation:
Program in Integrated Applied Mathematics, University of New Hampshire, Durham, NH 03824, USA Institute for Computational Engineering and Sciences, University of Texas at Austin, Austin, TX 78712, USA
Gregory P. Chini*
Affiliation:
Program in Integrated Applied Mathematics, University of New Hampshire, Durham, NH 03824, USA Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA
*
†Email address for correspondence: greg.chini@unh.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

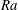High-Rayleigh-number ($Ra$) convection in an inclined two-dimensional porous layer is investigated using direct numerical simulations (DNS) and stability and variational upper-bound analyses. When the inclination angle 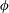$\unicode[STIX]{x1D719}$ of the layer satisfies $0^{\circ }<\unicode[STIX]{x1D719}\lesssim 25^{\circ }$, DNS confirm that the flow exhibits a three-region wall-normal asymptotic structure in accord with the strictly horizontal (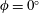$\unicode[STIX]{x1D719}=0^{\circ }$) case, except that as 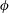$\unicode[STIX]{x1D719}$ is increased the time-mean spacing between neighbouring interior plumes also increases substantially. Both DNS and upper-bound analysis indicate that the heat transport enhancement factor (i.e. the Nusselt number) 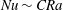$Nu\sim CRa$ with a 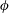$\unicode[STIX]{x1D719}$-dependent prefactor 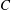$C$. When 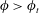$\unicode[STIX]{x1D719}>\unicode[STIX]{x1D719}_{t}$, however, where $30^{\circ }<\unicode[STIX]{x1D719}_{t}<32^{\circ }$ independently of 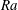$Ra$, the columnar flow structure is completely broken down: the flow transitions to a large-scale travelling-wave convective roll state, and the heat transport is significantly reduced. To better understand the physics of inclined porous medium convection at large 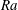$Ra$ and modest inclination angles, a spatial Floquet analysis is performed, yielding predictions of the linear stability of numerically computed, fully nonlinear steady convective states. The results show that there exist two types of instability when 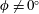$\unicode[STIX]{x1D719}\neq 0^{\circ }$: a bulk-mode instability and a wall-mode instability, consistent with previous findings for 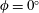$\unicode[STIX]{x1D719}=0^{\circ }$ (Wen et al., J. Fluid Mech., vol. 772, 2015, pp. 197–224). The background flow induced by the inclination of the layer intensifies the bulk-mode instability during its subsequent nonlinear evolution, thereby favouring increased spacing between the interior plumes relative to that observed in convection in a horizontal porous layer.

JFM classification

Convection: Convection in porous media Instability: Nonlinear instability Mathematical Foundations: Variational methods
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 837 , 25 February 2018 , pp. 670 - 702
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aidun, C. K. & Steen, P. H. 1987 Transition to oscillatory convective heat transfer in a fluid-saturated porous medium. J. Thermophys. Heat Transfer 1, 268–273.10.2514/3.38Google Scholar
Bories, S. A. & Combarnous, M. A. 1973 Natural convection in a sloping porous layer. J. Fluid Mech. 57, 63–79.10.1017/S0022112073001023Google Scholar
Bories, S. A., Combarnous, M. A. & Jaffrenou, J. Y. 1972 Observations des différentes formes d’écoulements thermoconvectifs dans une couche poreuse inclinée. C. R. Acad. Sci. Paris A 275, 857–860.Google Scholar
Bories, S. A. & Monferran, L. 1972 Condition de stabilité et échange thermique par convection naturelle dans une couche poreuse inclinée de grande extension. C. R. Acad. Sci. Paris  B 274, 4–7.Google Scholar
Boyd, J. P. 2000 Chebyshev and Fourier Spectral Methods, 2nd edn. Dover.Google Scholar
Caltagirone, J. P. & Bories, S. 1985 Solutions and stability criteria of natural convective flow in an inclined porous layer. J. Fluid Mech. 155, 267–287.Google Scholar
Caltagirone, J. P., Cloupeau, M. & Combarnous, M. 1971 Convection naturelle fluctuante dans une couche poreuse horizontale. C. R. Acad. Sci. Paris B 273, 833–836.Google Scholar
Doering, C. R. & Constantin, P. 1998 Bounds for heat transport in a porous layer. J. Fluid Mech. 376, 263–296.10.1017/S002211209800281XGoogle Scholar
Fu, X., Cueto-Felgueroso, L. & Juanes, R. 2013 Pattern formation and coarsening dynamics in three-dimensional convective mixing in porous media. Phil. Trans. R. Soc. Lond. A 371, 20120355.Google Scholar
Gill, A. E. 1969 A proof that convection in a porous vertical slab is stable. J. Fluid Mech. 35, 545–547.Google Scholar
Graham, M. D. & Steen, P. H. 1992 Strongly interacting traveling waves and quasiperiodic dynamics in porous medium convection. Physica D 54, 331–350.Google Scholar
Graham, M. D. & Steen, P. H. 1994 Plume formation and resonant bifurcations in porous-media convection. J. Fluid Mech. 272, 67–90.10.1017/S0022112094004386Google Scholar
Hewitt, D. R. & Lister, J. R. 2017 Stability of three-dimensional columnar convection in a porous medium. J. Fluid Mech. 829, 89–111.10.1017/jfm.2017.561Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2012 Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 108, 224503.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2013 Stability of columnar convection in a porous medium. J. Fluid Mech. 737, 205–231.10.1017/jfm.2013.559Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2014 High rayleigh number convection in a three-dimensional porous medium. J. Fluid Mech. 748, 879–895.Google Scholar
Horton, C. W. & Rogers, F. T. 1945 Convection currents in a porous medium. J. Appl. Phys. 16, 367–370.10.1063/1.1707601Google Scholar
Kaneko, T.1972 An experimental investigation of natural convection in porous media. MSc thesis, University of Calgary.Google Scholar
Kaneko, T., Mohtadi, M. F. & Aziz, K. 1974 An experimental study of natural convection in inclined porous media. Intl J. Heat Mass Transfer 17, 485–496.10.1016/0017-9310(74)90025-8Google Scholar
Kimura, S., Schubert, G. & Straus, J. M. 1986 Route to chaos in porous-medium thermal convection. J. Fluid Mech. 166, 305–324.Google Scholar
Kimura, S., Schubert, G. & Straus, J. M. 1987 Instabilities of steady, periodic, and quasi-periodic modes of convection in porous media. Trans. ASME J. Heat Transfer 109, 350–355.10.1115/1.3248087Google Scholar
Lapwood, E. R. 1948 Convection of a fluid in a porous medium. Proc. Camb. Phil. Soc. 44, 508–521.10.1017/S030500410002452XGoogle Scholar
MacMinn, C. W. & Juanes, R. 2013 Buoyant currents arrested by convective dissolution. Geophys. Res. Lett. 40, 2017–2022.Google Scholar
Metz, B., Davidson, O., de Coninck, H., Loos, M. & Meyer, L. 2005 IPCC Special Report on Carbon Dioxide Capture and Storage. Cambridge University Press.Google Scholar
Moya, S. L., Ramos, E. & Sen, M. 1987 Numerical study of natural convection in a tilted rectangular porous material. Intl J. Heat Mass Transfer 30, 741–756.10.1016/0017-9310(87)90204-3Google Scholar
Nield, D. A. & Bejan, A. 2013 Convection in Porous Media, 4th edn. Springer.Google Scholar
Nikitin, N. 2006 Third-order-accurate semi-implicit Runge–Kutta scheme for incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 51, 221–233.Google Scholar
Otero, J., Dontcheva, L. A., Johnston, H., Worthing, R. A., Kurganov, A., Petrova, G. & Doering, C. R. 2004 High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech. 500, 263–281.10.1017/S0022112003007298Google Scholar
Pau, G. S. H., Bell, J. B., Pruess, K., Almgren, A. S., Lijewski, M. J. & Zhang, K. 2010 High-resolution simulation and characterization of density-driven flow in CO2 storage in saline aquifers. Adv. Water Resour. 33, 443–455.Google Scholar
Peyret, Roger 2002 Spectral Methods for Incompressible Viscous Flow. Springer.10.1007/978-1-4757-6557-1Google Scholar
Phillips, O. M. 1991 Flow and Reactions in Permeable Rocks. Cambridge University Press.Google Scholar
Phillips, O. M. 2009 Geological Fluid Dynamics: Sub-surface Flow and Reactions. Cambridge University Press.Google Scholar
Rees, D. A. S. & Bassom, A. P. 2000 The onset of Darcy–Bénard convection in an inclined layer heated from below. Acta Mech. 144, 103–118.Google Scholar
Schubert, G. & Straus, J. M. 1982 Transitions in time-dependent thermal convection in fluid-saturated porous media. J. Fluid Mech. 121, 301–313.Google Scholar
Sen, M., Vasseur, P. & Robillard, L. 1987 Multiple steady states for unicellular natural convection in an inclined porous layer. Intl J. Heat Mass Transfer 30, 2097–2113.10.1016/0017-9310(87)90089-5Google Scholar
Trefethen, L. N. & Bau, D. III 1997 Numerical Linear Algebra. Society for Industrial and Applied Mathematics (SIAM).Google Scholar
Tsai, P. A., Riesing, K. & Stone, H. A. 2013 Density-driven convection enhanced by an inclined boundary: implications for geological CO 2 storage. Phys. Rev. E 87, 011003.Google Scholar
Voss, C. I., Simmons, C. T. & Robinson, N. I. 2010 Three-dimensional benchmark for variable-density flow and transport simulation: matching semi-analytic stability modes for steady unstable convection in an inclined porous box. Hydrogeol. J. 18, 5–23.Google Scholar
Wen, B.2015 Porous medium convection at large Rayleigh number: Studies of coherent structure, transport, and reduced dynamics. PhD thesis, University of New Hampshire.Google Scholar
Wen, B., Chini, G. P., Dianati, N. & Doering, C. R. 2013 Computational approaches to aspect-ratio-dependent upper bounds and heat flux in porous medium convection. Phys. Lett. A 377, 2931–2938.Google Scholar
Wen, B., Chini, G. P., Kerswell, R. R. & Doering, C. R. 2015a Time-stepping approach for solving upper-bound problems: Application to two-dimensional Rayleigh–Bénard convection. Phys. Rev. E 92, 043012.Google Scholar
Wen, B., Corson, L. T. & Chini, G. P. 2015b Structure and stability of steady porous medium convection at large Rayleigh number. J. Fluid Mech. 772, 197–224.Google Scholar